Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T14:39:08.761Z Has data issue: false hasContentIssue false
  • English
  • Français

On energetics and inertial-range scaling laws of two-dimensional magnetohydrodynamic turbulence

Published online by Cambridge University Press:  12 June 2012

Luke A. K. Blackbourn  and
Chuong V. Tran
Luke A. K. Blackbourn
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
Chuong V. Tran*
Affiliation:
School of Mathematics and Statistics, University of St Andrews, St Andrews KY16 9SS, UK
*
†Email address for correspondence: chuong@mcs.st-and.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We study two-dimensional magnetohydrodynamic turbulence, with an emphasis on its energetics and inertial-range scaling laws. A detailed spectral analysis shows that dynamo triads (those converting kinetic into magnetic energy) are associated with a direct magnetic energy flux while anti-dynamo triads (those converting magnetic into kinetic energy) are associated with an inverse magnetic energy flux. As both dynamo and anti-dynamo interacting triads are integral parts of the direct energy transfer, the anti-dynamo inverse flux partially neutralizes the dynamo direct flux, arguably resulting in relatively weak direct energy transfer and giving rise to dynamo saturation. This result is consistent with a qualitative prediction of energy transfer reduction due to Alfvén wave effects by the Iroshnikov–Kraichnan theory (which was originally formulated for magnetohydrodynamic turbulence in three dimensions). We numerically confirm the correlation between dynamo action and direct magnetic energy flux and investigate the applicability of quantitative aspects of the Iroshnikov–Kraichnan theory to the present case, particularly its predictions of energy equipartition and 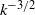spectra in the energy inertial range. It is found that for turbulence satisfying the Kraichnan condition of magnetic energy at large scales exceeding total energy in the inertial range, the kinetic energy spectrum, which is significantly shallower than 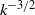, is shallower than its magnetic counterpart. This result suggests no energy equipartition. The total energy spectrum appears to depend on the energy composition of the turbulence but is clearly shallower than 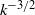for 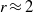, even at moderate resolutions. Here 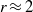is the magnetic-to-kinetic energy ratio during the stage when the turbulence can be considered fully developed. The implication of the present findings is discussed in conjunction with further numerical results on the dependence of the energy dissipation rate on resolution.

JFM classification

MHD and Electrohydrodynamics: MHD turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 703 , 25 July 2012 , pp. 238 - 254
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. J. Fluid Mech. 5, 113–133.CrossRefGoogle Scholar
2. Beresnyak, 2011 Spectral slope and Kolmogorov constant of MHD turbulence. Phys. Rev. Lett. 106, 075001.CrossRefGoogle ScholarPubMed
3. Biskamp, D. & Bremer, U. 1993 Dynamics and statistics of inverse cascade processes in 2D magnetohydrodynamic turbulence. Phys. Rev. Lett. 72, 3819–3822.CrossRefGoogle Scholar
4. Biskamp, D. & Welter, H. 1989 Dynamics of decaying two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 1, 1964–1979.CrossRefGoogle Scholar
5. Boldyrev, S. & Perez, J. C. 2009 Spectrum of weak magnetohydrodynamic turbulence. Phys. Rev. Lett. 103, 225010.CrossRefGoogle ScholarPubMed
6. Brandenburg, A. 2011 Nonlinear small-scale dynamos at low magnetic Prandtl numbers. Astrophys. J. 741, 92.CrossRefGoogle Scholar
7. Cattaneo, F. & Tobias, S. M. 2009 Dynamo properties of the turbulent velocity field of a saturated dynamo. J. Fluid Mech. 621, 205–214.CrossRefGoogle Scholar
8. Dritschel, D. G., Scott, R. K., Macaskill, C., Gottwald, G. A. & Tran, C. V. 2008 Unifying scaling theory for vortex dynamics in two-dimensional turbulence. Phys. Rev. Lett. 101, 094501.CrossRefGoogle ScholarPubMed
9. Fyfe, D. & Montgomery, D. 1976 High-beta turbulence in two-dimensional magnetohydrodynamics. J. Plasma Phys. 16, 181–191.CrossRefGoogle Scholar
10. Galtier, S., Pouquet, A. & Mangeney, A. 2005 Spectral scaling laws for incompressible anisotropic magnetohydrodynamic turbulence. Phys. Plasmas 12, 092310.CrossRefGoogle Scholar
11. Goldreich, P. & Sridhar, S. 1995 Toward a theory of interstellar turbulence. II. Strong Alfvénic turbulence. Astrophys. J. 438, 763–775.CrossRefGoogle Scholar
12. Grappin, R., Pouquet, A. & Leorat, J. 1983 Dependence of MHD turbulence spectra on the velocity field-magnetic field correlation. Astron. Astrophys. 126, 51–58.Google Scholar
13. Haugen, N. E. L., Brandenburg, A. & Dobler, W. 2003 Is nonhelical hydromagnetic turbulence peaked at small scales? Astrophys. J. 597, L141–L144.CrossRefGoogle Scholar
14. Iroshnikov, P. S. 1964 Turbulence of a conducting fluid in a strong magnetic field. Sov. Astron. 7, 566–571.Google Scholar
15. Kim, E.-J. & Dubrulle, B. 2002 Are the energy and magnetic potential cascades direct or inverse in 2D MHD turbulence. Physica D 165, 213–227.CrossRefGoogle Scholar
16. Kraichnan, R. H. 1965 Inertial-range spectrum of hydromagnetic turbulence. Phys. Fluids 8, 1385–1387.CrossRefGoogle Scholar
17. Lee, E., Brachet, M. E., Pouquet, A., Mininni, P. D. & Rosenberg, D. 2010 Lack of universality in decaying magnetohydrodynamic turbulence. Phys. Rev. E 81, 016318.CrossRefGoogle ScholarPubMed
18. Loureiro, N. F., Uzdensky, D. A., Schekochihin, A. A., Cowley, S. C. & Yousef, T. A. 2009 Turbulent magnetic reconnection in two dimensions. Mon. Not. R. Astron. Soc. 399, L146–L150.CrossRefGoogle Scholar
19. Mininni, P. D., Pouquet, A. G. & Montgomery, D. C. 2006 Small-scale structures in three-dimensional magnetohydrodynamic turbulence. Phys. Rev. Lett. 97, 244503.CrossRefGoogle ScholarPubMed
20. Moffatt, K. H. 1967 On the suppression of turbulence by a uniform magnetic field. J. Fluid Mech. 28, 571–592.CrossRefGoogle Scholar
21. Müller, W. & Grappin, R. 2005 Spectral energy dynamics in magnetohydrodynamic turbulence. Phys. Rev. Lett. 95, 114502.CrossRefGoogle ScholarPubMed
22. Ng, C. S., Bhattacharjee, A., Munsi, D., Isenberg, P. A. & Smith, C. W. 2010 Kolmogorov versus Irosnikov–Kraichnan spectra: consequence for ion heating in the solar wind. J. Geophys. Res. 115, A02101.Google Scholar
23. Ohkitani, K. 2006 A note on regularity conditions on ideal magnetohydrodynamic equations. Phys. Plasmas 13, 044504.CrossRefGoogle Scholar
24. Podesta, J. J., Roberts, D. A. & Goldstein, M. L. 2007 Spectral exponents of kinetic and magnetic energy spectra in solar wind turbulence. Astrophys. J. 664, 543–548.CrossRefGoogle Scholar
25. Politano, H., Pouquet, A. & Sulem, P. L. 1989 Inertial ranges and resistive instabilities in two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 1, 2330–2339.CrossRefGoogle Scholar
26. Pouquet, A. 1978 On two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 88, 1–16.CrossRefGoogle Scholar
27. Sridhar, S. & Goldreich, P. 1994 Toward a theory of interstellar turbulence. I. Weak Alfvénic turbulence. Astrophys. J. 432, 612–621.CrossRefGoogle Scholar
28. Servidio, S., Matthaeus, W. H., Shay, M. A., Dmitruk, P., Cassak, P. A. & Wan, M. 2010 Statistics of magnetic reconnection in two-dimensional magnetohydrodynamic turbulence. Phys. Plasmas 17, 032315.CrossRefGoogle Scholar
29. Tessein, J. A., Smith, C. W., MacBride, B. T., Matthaeus, W. H., Forman, M. A. & Borovsky, J. E. 2009 Spectral indices for multi-dimensional interplanetary turbulence at 1 AU. Astrophys. J. 692, 684–693.CrossRefGoogle Scholar
30. Tobias, S. M. & Cattaneo, F. 2008 Dynamo action in complex flows: the quick and the fast. J. Fluid Mech. 601, 101–122.CrossRefGoogle Scholar
31. Tran, C. V. 2008 Local transfer and spectra of a diffusive field advected by large-scale imcompressible flows. Phys. Rev. E 78, 036310.CrossRefGoogle ScholarPubMed
32. Tran, C. V. & Blackbourn, L. A. K. 2012 A dynamical systems approach to fluid turbulence. Fluid Dyn. Res. 44, 031417.CrossRefGoogle Scholar
33. Tran, C. V., Blackbourn, L. A. K. & Scott, R. K. 2011 Number of degrees of freedom and energy spectrum of surface quasi-geostrophic turbulence. J. Fluid Mech. 684, 427–440.CrossRefGoogle Scholar
34. Tran, C. V. & Dritschel, D. G. 2006 Large-scale dynamics in two-dimensional Euler and surface quasigeostrophic flows. Phys. Fluids 18, 121703.CrossRefGoogle Scholar
35. Tran, C. V. & Dritschel, D. G. 2010 Energy dissipation and resolution of steep gradients in one-dimensional Burgers flows. Phys. Fluids 22, 037102.CrossRefGoogle Scholar
36. Tran, C. V., Dritschel, D. G. & Scott, R. K. 2010 Effective degrees of nonlinearity in a family of generalized models of two-dimensional turbulence. Phys. Rev. E 81, 016301.CrossRefGoogle Scholar
37. Tran, C. V. & Yu, X. 2012 Bounds for the number of degrees of freedom of magnetohydrodynamics turbulence in two and three dimensions. Phys. Rev. E (provisionally accepted).CrossRefGoogle Scholar
38. Verma, M. K., Roberts, D. A., Goldstein, M. L., Gosh, S. & Stribling, W. T. 1996 A numerical study of the nonlinear cascade of energy in magnetohydrodynamic turbulence. J. Geophys. Res. 101, 21619–21625.CrossRefGoogle Scholar