Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chan, Kit H.
Liao, Xinhao
and
Zhang, Keke
2011.
Simulations of fluid motion in ellipsoidal planetary cores driven by longitudinal libration.
Physics of the Earth and Planetary Interiors,
Vol. 187,
Issue. 3-4,
p.
391.
Chan, Kit H.
Liao, Xinhao
and
Zhang, Keke
2011.
Simulations of fluid motion in spheroidal planetary cores driven by latitudinal libration.
Physics of the Earth and Planetary Interiors,
Vol. 187,
Issue. 3-4,
p.
404.
Cébron, D.
Le Bars, M.
Noir, J.
and
Aurnou, J. M.
2012.
Libration driven elliptical instability.
Physics of Fluids,
Vol. 24,
Issue. 6,
Noir, J.
Cébron, D.
Le Bars, M.
Sauret, A.
and
Aurnou, J.M.
2012.
Experimental study of libration-driven zonal flows in non-axisymmetric containers.
Physics of the Earth and Planetary Interiors,
Vol. 204-205,
Issue. ,
p.
1.
Cebron, D.
Le Bars, M.
Moutou, C.
and
Le Gal, P.
2012.
Elliptical instability in terrestrial planets and moons.
Astronomy & Astrophysics,
Vol. 539,
Issue. ,
p.
A78.
Sauret, Alban
Cébron, David
Le Bars, Michael
and
Le Dizès, Stéphane
2012.
Fluid flows in a librating cylinder.
Physics of Fluids,
Vol. 24,
Issue. 2,
Chan, Kit H.
2012.
Nonlinear flow within a triaxial ellipsoidal planet driven by combined longitudinal and latitudinal libration.
Physics of the Earth and Planetary Interiors,
Vol. 194-195,
Issue. ,
p.
64.
Zhang, Keke
Chan, Kit H.
and
Liao, Xinhao
2012.
Asymptotic theory of resonant flow in a spheroidal cavity driven by latitudinal libration.
Journal of Fluid Mechanics,
Vol. 692,
Issue. ,
p.
420.
Zhang, Keke
Chan, Kit H.
Liao, Xinhao
and
Aurnou, Jonathan M.
2013.
The non-resonant response of fluid in a rapidly rotating sphere undergoing longitudinal libration.
Journal of Fluid Mechanics,
Vol. 720,
Issue. ,
p.
212.
Sauret, Alban
and
Le Dizès, Stéphane
2013.
Libration-induced mean flow in a spherical shell.
Journal of Fluid Mechanics,
Vol. 718,
Issue. ,
p.
181.
Koch, S
Harlander, U
Egbers, C
and
Hollerbach, R
2013.
Inertial waves in a spherical shell induced by librations of the inner sphere: experimental and numerical results.
Fluid Dynamics Research,
Vol. 45,
Issue. 3,
p.
035504.
Wu, Cheng-Chin
and
Roberts, Paul H.
2013.
On a dynamo driven topographically by longitudinal libration.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 107,
Issue. 1-2,
p.
20.
Le Bars, Michael
2014.
Experimental and Computational Fluid Mechanics.
p.
83.
Grannan, A. M.
Le Bars, M.
Cébron, D.
and
Aurnou, J. M.
2014.
Experimental study of global-scale turbulence in a librating ellipsoid.
Physics of Fluids,
Vol. 26,
Issue. 12,
Sauret, Alban
Le Bars, Michael
and
Le Gal, Patrice
2014.
Tide‐driven shear instability in planetary liquid cores.
Geophysical Research Letters,
Vol. 41,
Issue. 17,
p.
6078.
Roberts, P.H.
2015.
Treatise on Geophysics.
p.
57.
Le Bars, Michael
Cébron, David
and
Le Gal, Patrice
2015.
Flows Driven by Libration, Precession, and Tides.
Annual Review of Fluid Mechanics,
Vol. 47,
Issue. 1,
p.
163.
Favier, B.
Grannan, A. M.
Le Bars, M.
and
Aurnou, J. M.
2015.
Generation and maintenance of bulk turbulence by libration-driven elliptical instability.
Physics of Fluids,
Vol. 27,
Issue. 6,
Sauret, A
2015.
Mean zonal flow generated by azimuthal harmonic forcing in a rotating cylinder.
Fluid Dynamics Research,
Vol. 47,
Issue. 3,
p.
035506.
Le Bars, Michael
2016.
Flows driven by libration, precession, and tides in planetary cores.
Physical Review Fluids,
Vol. 1,
Issue. 6,
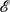 is investigated. The ellipsoid rotates with an angular velocity Ω0(1 + δsin
is investigated. The ellipsoid rotates with an angular velocity Ω0(1 + δsin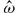 t), where Ω0 is the mean rate of rotation,
t), where Ω0 is the mean rate of rotation, 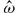 is the libration frequency and Ω0δ represents the amplitude of longitudinal libration. When δ ≪
is the libration frequency and Ω0δ represents the amplitude of longitudinal libration. When δ ≪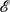 2 and E1/2 ≪
2 and E1/2 ≪ 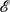 2 ≪ 1, where E is the Ekman number defined as E = ν/(a2Ω0), an explicit analytical solution describing fluid motion in librating ellipsoids is derived for any size of the libration frequency
2 ≪ 1, where E is the Ekman number defined as E = ν/(a2Ω0), an explicit analytical solution describing fluid motion in librating ellipsoids is derived for any size of the libration frequency 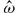 . Three-dimensional numerical simulations of the same problem are also performed, revealing the generation of mean zonal flow in librating ellipsoidal cavities and showing a satisfactory agreement between the asymptotic and numerical analyses.
. Three-dimensional numerical simulations of the same problem are also performed, revealing the generation of mean zonal flow in librating ellipsoidal cavities and showing a satisfactory agreement between the asymptotic and numerical analyses.
