Article contents
On mathematical approaches to modelling slender liquid jets with a curved trajectory
Published online by Cambridge University Press: 13 April 2018
Abstract
Slender liquid jets that have a curved trajectory have been examined in a range of papers using a method introduced in Wallwork et al. (Proc. IUTAM Symp. on Free-Surface Flows, 2000, Kluwer; J. Fluid Mech., vol. 459, 2002, pp. 43–65) and Decent et al. (J. Engng Maths, vol. 42, 2002, pp. 265–282), for jets that emerge from an orifice on the surface of a rotating cylindrical container, successfully comparing computational results to measurements arising from laboratory experiments. Wallwork et al. (2000, 2002) and Decent et al. (2002) based their analyses on the slenderness of the jet, and neglected the torsion of the centreline of the jet, which is valid since in most situations examined the torsion is zero or small. Shikhmurzaev & Sisoev (J. Fluid Mech., vol. 819, 2017, pp. 352–400) used differential geometry and incorporated the torsion. This paper shows that these two methods produce identical results at leading order when the torsion is zero or when the torsion is 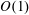 $O(1)$, in an asymptotic framework based upon the slenderness of the jet, and shows that the method of Wallwork et al. (2000, 2002) and Decent et al. (2002) is accurate for parameters corresponding to scenarios previously examined and also when the torsion is
$O(1)$, in an asymptotic framework based upon the slenderness of the jet, and shows that the method of Wallwork et al. (2000, 2002) and Decent et al. (2002) is accurate for parameters corresponding to scenarios previously examined and also when the torsion is  $O(1)$. It is shown that the method of Shikhmurzaev & Sisoev (2017) should be used when the torsion is asymptotically large or when the jet is not slender.
$O(1)$. It is shown that the method of Shikhmurzaev & Sisoev (2017) should be used when the torsion is asymptotically large or when the jet is not slender.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 12
- Cited by

