Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T16:03:56.513Z Has data issue: false hasContentIssue false
  • English
  • Français

On multiphase turbulence models for collisional fluid–particle flows

Published online by Cambridge University Press:  21 February 2014

Rodney O. Fox
Get access Rights & Permissions [Opens in a new window]

Abstract

Starting from a kinetic theory (KT) model for monodisperse granular flow, the exact Reynolds-averaged (RA) equations are derived for the particle phase in a collisional fluid–particle flow. The corresponding equations for a constant-density fluid phase are derived from a model that includes drag and buoyancy coupling with the particle phase. The fully coupled macroscale/hydrodynamic model, rigorously derived from a kinetic equation for the particles, is written in terms of the particle-phase volume fraction, the particle-phase velocity and the granular temperature (or total granular energy). As derived from the hydrodynamic model, the RA turbulence model solves for the RA particle-phase volume fraction, the phase-averaged (PA) particle-phase velocity, the PA granular temperature and the PA turbulent kinetic energy of the particle phase. 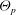Thus, unlike in most previous derivations of macroscale turbulence models for moderately dense granular flows, a clear distinction is made between the PA granular temperature $\Theta _\textit {p}$, which appears in the KT constitutive relations, and the particle-phase turbulent kinetic energy $k_\textit {p}$, which appears in the turbulent transport coefficients. The exact RA equations contain unclosed terms due to nonlinearities in the hydrodynamic model and we briefly discuss the available closures for these terms. Finally, we demonstrate by comparing model predictions with direct numerical simulation results that even for non-collisional fluid–particle flows it is necessary to provide separate models for 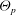$\Theta _\textit {p}$ and 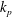$k_\textit {p}$ in order to correctly account for the effect of the particle Stokes number and mass loading.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulence modelling
Type
Papers
Information
Journal of Fluid Mechanics , Volume 742 , 10 March 2014 , pp. 368 - 424
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

̄eferences

Agrawal, K., Loezos, P. N., Syamlal, M. & Sundaresan, S. 2001 The role of meso-scale structures in rapid gas–solids flows. J. Fluid Mech. 445, 151–181.Google Scholar
Ahmadi, G. & Ma, D. 1990 A thermodynamical formulation for dispersed multiphase turbulent flows: I. Basic theory. Intl J. Multiphase Flow 16, 323–340.Google Scholar
Ahmed, A. M. & Elghobashi, S. 2000 On the mechanisms of modifying the structure of turbulent homogeneous shear flows by dispersed particles. Phys. Fluids 12, 2906–2930.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flows. Annu. Rev. Fluid Mech. 42, 111–133.Google Scholar
Benavides, A. & van Wachem, B. 2008 Numerical simulation and validation of dilute turbulent gas–particle flow with inelastic collisions and turbulence modulation. Powder Technol. 182, 294–306.Google Scholar
Besnard, D. C. & Harlow, F. H. 1985 Turbulence in two-fluid incompressible flows. NASA Tech. Rep. LA-10187MS. Los Alamos National Laboratory.Google Scholar
Bragg, A., Swailes, D. C. & Skartlien, R. 2012 Particle transport in a turbulent boundary layer: non-local closures for particle dispersion tensors accounting for particle–wall interactions. Phys. Fluids 24, 103304.Google Scholar
Canuto, V. M. 1997 Compressible turbulence. Astrophys. J. 482, 827–851.Google Scholar
Cao, J. & Ahmadi, G. 1995 Gas–particle two-phase turbulent flow in a vertical duct. Intl J. Multiphase Flow 21, 1203–1228.Google Scholar
Capecelatro, J. & Desjardins, O. 2013 An Euler–Lagrange strategy for simulating particle-laden flows. J. Comput. Phys. 238, 1–31.Google Scholar
Cartellier, A., Andreotti, M. & Sechet, P. 2009 Induced agitation in homogeneous bubbly flows at moderate particle Reynolds number. Phys. Rev. 80, 065301(R).Google Scholar
Chao, Z., Wang, Y., Jakobsen, J. P., Fernandino, M. & Jakobsen, H. A. 2011 Derivation and validation of a binary multi-fluid Eulerian model for fluidized beds. Chem. Engng Sci. 66, 3605–3616.Google Scholar
Chao, Z., Wang, Y., Jakobsen, J. P., Fernandino, M. & Jakobsen, H. A. 2012 Investigation of the particle–particle drag in a dense binary fluidized beds. Powder Technol. 224, 311–322.Google Scholar
Cheng, Y., Guo, Y., Wei, F., Jin, Y. & Lin, W. 1999 Modeling the hydrodynamics of downer reactors based on kinetic theory. Chem. Engng Sci. 54, 2019–2027.CrossRefGoogle Scholar
Crowe, C. T., Troutt, T. R. & Chung, J. N. 1996 Numerical models for two-phase turbulent flows. Annu. Rev. Fluid Mech. 28, 11–43.CrossRefGoogle Scholar
Dasgupta, S., Jackson, R. & Sundaresan, S. 1994 Turbulent gas–particle flow in vertical risers. AIChE J. 40, 215–228.CrossRefGoogle Scholar
Dasgupta, S., Jackson, R. & Sundaresan, S. 1998 Gas-particle flow in vertical pipes with high mass loading of particles. Powder Technol. 96, 6–23.Google Scholar
Dufek, J. & Bergantz, G. W. 2007 Suspended load and bed-load transport of particle-laden gravity currents: the role of particle–bed interaction. Theor. Comput. Fluid Dyn. 21, 119–145.CrossRefGoogle Scholar
Elgobashi, S. E. & Abou-Arab, T. W. 1983 A two-equation turbulence model for two-phase flows. Phys. Fluids 26, 931–938.Google Scholar
Février, P., Simonin, O. & Squires, K. D. 2005 Partitioning of particle velocities in gas–solid turbulent flows into a continuous field and a spatially uncorrelated random distribution: theoretical formalism and numerical study. J. Fluid Mech. 533, 1–46.CrossRefGoogle Scholar
Fox, R. O. 2003 Computational Models for Turbulent Reacting Flows. Cambridge University Press.Google Scholar
Fox, R. O. 2008 A quadrature-based third-order moment method for dilute gas–particle flows. J. Comput. Phys. 227, 6313–6350.Google Scholar
Fox, R. O. 2012 Large-eddy-simulation tools for multiphase flows. Annu. Rev. Fluid Mech. 44, 47–76.CrossRefGoogle Scholar
Fox, R. O. 2014 Quadrature-based moment methods for polydisperse multiphase flows. In Stochastic Methods in Fluid Mechanics (ed. Chibbaro, S. & Minier, J. P.), CISM, vol. 548, pp. 87–136. Springer.CrossRefGoogle Scholar
Fox, R. O. & Vedula, P. 2010 Quadrature-based moment model for moderately dense polydisperse gas–particle flows. Ind. Engng Chem. Res. 49, 5174–5187.Google Scholar
Garnier, C., Lance, M. & Marié, J. L. 2002 Measurement of local flow characteristics in buoyancy-driven bubbly flow at high void fraction. Exp. Therm. Fluid Sci. 26, 811–815.Google Scholar
Garzó, V., Tenneti, S., Subramaniam, S. & Hrenya, C. M. 2012 Enskog kinetic theory for monodisperse gas–solid flows. J. Fluid Mech. 712, 129–168.Google Scholar
He, H. & Simonin, O. 1993 Non-equilibrium prediction of the particle-phase stress tensor in vertical pneumatic conveying. In Gas–Solid Flows-1993 ASME FED, vol. 166, pp. 253–263. ASME.Google Scholar
Hrenya, C. M. & Sinclair, J. L. 1997 Effects of particle-phase turbulence in gas–solid flows. AIChE J. 43, 853–869.CrossRefGoogle Scholar
Huilin, L., Gidaspow, D. & Manger, E. 2001 Kinetic theory of fluidized binary granular mixtures. Phys. Rev. E 64, 061301.Google Scholar
Igci, Y., Andrews, A. T., Sundaresan, S., Pannala, S. & O’Brien, T. 2008 Filtered two-fluid models for fluidized gas–particle suspensions. AIChE J. 54, 1431–1448.Google Scholar
IJzermans, R. H. A., Meneguz, E. & Reeks, M. W. 2010 Segregation of particles in incompressible random flows: singularities, intermittency and random uncorrelated motion. J. Fluid Mech. 653, 99–136.CrossRefGoogle Scholar
Jackson, R. 2000 Dynamics of Fluidized Particles. Cambridge University Press.Google Scholar
Jenkins, J. T. & Savage, S. B. 1983 A theory for the rapid flow of identical, smooth, nearly elastic spherical particles. J. Fluid Mech. 130, 187–202.Google Scholar
Jiang, Y. Y. & Zhang, P. 2012 Numerical investigation of slush nitrogen flow in a horizontal pipe. Chem. Engng Sci. 73, 169–180.CrossRefGoogle Scholar
Johnson, B. M. & Schilling, O. 2011 Reynolds-averaged Navier–Stokes model predictions of linear instability. I: Buoyancy- and shear-driven flows. J. Turbul. 12 (36), 1–38.Google Scholar
Kaufmann, A., Moreau, M., Simonin, O. & Helie, J. 2008 Comparison between Lagrangian and mesoscopic Eulerian modeling approaches for inertial particles suspended in decaying isotropic turbulence. J. Comput. Phys. 227, 6448–6472.CrossRefGoogle Scholar
Lun, C. K. K., Savage, S. B., Jeffery, D. J. & Chepurniy, N. 1984 Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field. J. Fluid Mech. 140, 223–256.Google Scholar
Marchisio, D. L. & Fox, R. O. 2013 Computational Models for Polydisperse Particulate and Multiphase Systems. Cambridge University Press.CrossRefGoogle Scholar
Maxey, R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Maxey, R. & Riley, J. 1983 Equation of motion of a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
Milioli, C. C., Milioli, F. E., Holloway, W., Agrawal, K. & Sundaresan, S. 2013 Filtered two-fluid models of fluidized gas–particle flows: new constitutive relations. AIChE J. 59, 3265–3275.Google Scholar
Minier, J. P. & Peirano, E. 2001 The PDF approach to turbulent polydispersed two-phase flows. Phys. Rep. 352, 1–214.Google Scholar
Ozel, A., Fede, P. & Simonin, O. 2013 Development of filtered Euler–Euler two-phase model for circulating fluidised bed: high resolution simulation, formulation and a priori analyses. Intl J. Multiphase Flow 55, 43–63.Google Scholar
Pai, M. G. & Subramaniam, S. 2012 Two-way coupled stochastic model for dispersion of inertial particles in turbulence. J. Fluid Mech. 700, 29–62.CrossRefGoogle Scholar
Parmentier, J.-F., Simonin, O. & Delsart, O. 2012 A functional subgrid drift velocity model for filtered drag prediction in dense fluidized bed. AIChE J. 58, 1084–1098.Google Scholar
Passalacqua, A., Fox, R. O., Garg, R. & Subramaniam, S. 2010 A fully coupled quadrature-based moment method for dilute to moderately dilute fluid–particle flows. Chem. Engng Sci. 65, 2267–2283.CrossRefGoogle Scholar
Passalacqua, A., Galvin, J. E., Vedula, P., Hrenya, C. M. & Fox, R. O. 2011 A quadrature-based kinetic model for dilute non-isothermal granular flows. Commun. Comput. Phys. 10, 216–252.Google Scholar
Peirano, E. & Leckner, B. 1998 Fundamentals of turbulent gas–solid flows applied to circulating fluidized bed combustion. Prog. Energy Combust. Sci. 24, 259–296.Google Scholar
Peters, N. 2000 Turbulent Combustion. Cambridge University Press.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rao, A., Curtis, J. S., Hancock, B. C. & Wassgren, C. 2012 Numerical simulation of dilute turbulent gas–particle flow with turbulence modulation. AIChE J. 58, 1381–1396.Google Scholar
Reeks, M. W. 1991 On a kinetic-equation for the transport of particles in turbulent flow. Phys. Fluids A 3, 446–456.Google Scholar
Riboux, G., Risso, F. & Legendre, D. 2010 Experimental characterization of the agitation generated by bubbles rising at high Reynolds number. J. Fluid Mech. 643, 509–539.Google Scholar
Rumsey, C. L. 2009 Compressibility considerations for $k$ – $\omega $ turbulence models in hypersonic boundary layer applications. Tech. Rep. NASA/TM-2009-215705. NASA Center for AeroSpace Information.Google Scholar
Sato, Y. & Sekoguchi, K. 1975 Liquid velocity distribution in two-phase bubble flow. Intl J. Multiphase Flow 2, 75–95.CrossRefGoogle Scholar
Schwarzkopf, J. D., Livescu, D., Gore, R. A., Rauenzahn, R. M. & Ristorcelli, J. R. 2011 Application of a second-moment closure model to mixing processes involving multicomponent miscible fluids. J. Turbul. 12 (49), 1–35.Google Scholar
Simonin, O. 1996 Continuum modeling of dispersed turbulent two-phase flows. Part I: General model description. Tech. Rep. Lecture Series. von Kármán Institute of Fluid Dynamics.Google Scholar
Simonin, O., Deutsch, E. & Minier, J. P. 1993 Eulerian predictions of the fluid/particle correlated motion in turbulent two-phase flows. Appl. Sci. Res. 51, 275–283.Google Scholar
Sinclair, J. & Mallo, T. 1998 Describing particle–turbulence interaction in a two-fluid modeling framework. Proceedings of FEDSM’98: ASME Fluids Engineering Division Summer Meeting. vol. 4. pp. 7–14. ASME.Google Scholar
Sinclair, J. L. & Jackson, R. 1989 Gas–particle flow in a vertical pipe with particle–particle interactions. AIChE J. 35, 1473–1486.CrossRefGoogle Scholar
Sundaram, S. & Collins, L. C. 1994 Spectrum of density fluctuations in a particle–fluid system. I. Monodisperse spheres. Intl J. Multiphase Flow 20, 1021–1037.Google Scholar
Sundaram, S. & Collins, L. C. 1999 A numerical study of the modulation of isotropic turbulence by suspended particles. J. Fluid Mech. 379, 105–143.Google Scholar
Sundaresan, S. 2000 Modeling the hydrodynamics of multiphase flow reactors: current status and challenges. AIChE J. 46, 1102–1105.Google Scholar
Tartan, M. & Gidaspow, D. 2004 Measurement of granular temperature and stresses in risers. AIChE J. 50, 1760–1775.CrossRefGoogle Scholar
Tchen, C. M.1947 Mean value and correlation problems connected with the motion of small particles suspended in a turbulent fluid. PhD thesis, University of Delft, The Hague.Google Scholar
Tenneti, S., Garg, R., Hrenya, C. M., Fox, R. O. & Subramaniam, S. 2010 Direct numerical simulation of gas–solid suspensions at moderate Reynolds number: quantifying the coupling between hydrodynamic forces and particle velocity fluctuations. Powder Technol. 203, 57–69.CrossRefGoogle Scholar
Wilcox, D. W. 2006 Turbulence Modeling for CFD, 3rd edn. DCW Industries.Google Scholar
Xu, Y. & Subramaniam, S. 2006 A multiscale model for dilute turbulent gas–particle flows based on the equilibration of energy concept. Phys. Fluids 18, 033301.Google Scholar
Xu, Y. & Subramaniam, S. 2007 Consistent modeling of interphase turbulent kinetic energy transfer in particle-laden turbulent flows. Phys. Fluids 19, 085101.Google Scholar
Yin, X., Zenk, J. R., Mitrano, P. P. & Hrenya, C. M. 2013 Impact of collisional versus viscous dissipation on flow instabilities in gas–solid systems. J. Fluid Mech. 727, R2.Google Scholar
Zaichik, L. I., Alipchenkov, V. M. & Sinaiski, E. G. 2008 Particles in Turbulent Flows. Wiley-VCH.Google Scholar
Zaichik, L. I., Simonin, O. & Alipchenkov, V. M. 2010 Turbulent collision rates of arbitrary-density particles. Intl J. Heat Mass Transfer 53, 1613–1620.Google Scholar
Zeng, Zh. X. & Zhou, L. X. 2006 A two-scale second-order moment particle turbulence model and simulation of dense gas–particle flows in a riser. Powder Technol. 162, 27–32.Google Scholar
Zheng, Y., Wan, X., Qian, Z., Wei, F. & Jin, Y. 2001 Numerical simulation of the gas–particle turbulent flow in riser reactor based on $k$ – $\varepsilon $ – $k_p$ – $\varepsilon _p$ – $\theta $ two-fluid model. Chem. Engng Sci. 56, 6813–6822.Google Scholar
Zuber, N. & Findlay, J. A. 1965 Average volumetric concentration in two-phase flow systems. Trans. ASME C: J. Heat Transfer 87, 453–468.CrossRefGoogle Scholar