Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-10T09:31:20.815Z Has data issue: false hasContentIssue false
  • English
  • Français

On standing gravity wave-depression cavity collapse and jetting

Published online by Cambridge University Press:  05 March 2019

D. Krishna Raja ,
S. P. Das Open the ORCID record for S. P. Das [Opens in a new window]  and
E. J. Hopfinger
D. Krishna Raja
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
S. P. Das*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Madras, Chennai 600036, India
E. J. Hopfinger
Affiliation:
LEGI, CNRS/UGA, BP 53, 38041 Grenoble Cedex 9, France
*
†Email address for correspondence: spdas@iitm.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Parametrically forced gravity waves can give rise to high-velocity surface jets via the wave-depression cavity implosion. The present results have been obtained in circular cylindrical containers of 10 and 15 cm in diameter (Bond number of order 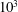$10^{3}$) in the large fluid depth limit. First, the phase diagrams of instability threshold and wave breaking conditions are determined for the working fluid used, here water with 1 % detergent added. The collapse of the wave-depression cavity is found to be self-similar. The exponent $\unicode[STIX]{x1D6FC}$ of the variation of the cavity radius 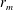$r_{m}$ with time $\unicode[STIX]{x1D70F}$, in the form 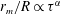$r_{m}/R\propto \unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D6FC}}$, is close to 0.5, indicative of inertial collapse, followed by a viscous cut-off of 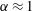$\unicode[STIX]{x1D6FC}\approx 1$. This supports a Froude number scaling of the surface jet velocity caused by cavity collapse. The dimensionless jet velocity scales with the cavity depth that is shown to be proportional to the last stable wave amplitude. It can be expressed by a power law or in terms of finite time singularity related to a singular wave amplitude that sets the transition from a non-pinching to pinch-off cavity collapse scenario. In terms of forcing amplitude, cavity collapse and jetting are found to occur in bands of events of non-pinching and pinching of a bubble at the cavity base. At large forcing amplitudes, incomplete cavity collapse and splashing can occur and, at even larger forcing amplitudes, wave growth is again stable up to the singular wave amplitude. When the cavity is formed, an impulse model shows the importance of the singular cavity diameter that determines the strength of the impulse.

JFM classification

Waves/Free-surface Flows: Faraday waves Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Wave breaking
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 866 , 10 May 2019 , pp. 112 - 131
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, T. B. & Ursell, F. 1954 The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. Lond. A 225, 505–515.Google Scholar
Bergmann, R., van der Meer, D., Stijnman, M., Sandtke, M., Prosperetti, A. & Lohse, D. 2006 Giant bubble pinch-off. Phys. Rev. Lett. 96, 154505.Google Scholar
Burton, J. C. & Taborek, P. 2007 Role of dimensionality and axisymmetry in fluid pinch-off and coalescence. Phys. Rev. Lett. 98, 224502.Google Scholar
Burton, J. C., Waldrep, R. & Taborek, P. 2005 Scaling and instabilities in bubble pinch-off. Phys. Rev. Lett. 94, 184502.Google Scholar
Cooker, M. J. & Peregrine, D. H. 1991 A model for breaking wave impact pressures. In Coastal Engineering 1990, pp. 1473–1486. American Society of Civil Engineers.Google Scholar
Cooker, M. J. & Peregrine, D. H. 1995 Pressure-impulse theory for liquid impact problems. J. Fluid Mech. 297, 193–214.Google Scholar
Das, S. P. & Hopfinger, E. J. 2008 Parametrically forced gravity waves in a circular cylinder and finite-time singularity. J. Fluid Mech. 599, 205–228.Google Scholar
Das, S. P. & Hopfinger, E. J. 2009 Mass transfer enhancement by gravity waves at a liquid–vapour interface. Intl J. Heat Mass Transfer 52, 1400–1411.Google Scholar
Denner, F. 2016 Frequency dispersion of small-amplitude capillary waves in viscous fluids. Phys. Rev. E 94, 023110.Google Scholar
Ding, H., Chen, B. Q., Liu, H. R., Zhang, C. Y., Gao, P. & Lu, X. Y. 2015 On the contact-line pinning in cavity formation during solid–liquid impact. J. Fluid Mech. 783, 504–525.Google Scholar
Edwards, W. S. & Fauve, S. 1994 Patterns and quasi-patterns in the Faraday experiment. J. Fluid Mech. 278, 123–148.Google Scholar
Eggers, J., Fontelos, M. A., Leppinen, D. & Snoeijer, J. H. 2007 Theory of the collapsing axisymmetric cavity. Phys. Rev. Lett. 98, 094502.Google Scholar
Faltinsen, O. M., Rognebakke, O. F., Lukovsky, I. A. & Timokha, A. N. 2000 Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth. J. Fluid Mech. 407, 201–234.Google Scholar
Gordillo, J. M., Sevilla, A., Rodríguez-Rodríguez, J. & Martinez-Bazan, C. 2005 Axisymmetric bubble pinch-off at high Reynolds numbers. Phys. Rev. Lett. 95, 194501.Google Scholar
Henderson, D. M. & Miles, J. W. 1990 Single-mode Faraday waves in small cylinders. J. Fluid Mech. 213, 95–109.Google Scholar
Hürhnerfuss, H., Lange, P. A. & Walter, W. 1985 Relaxation effects in monolayers and their contribution to water wave damping. II. The Marangoni phenomenon and gravity wave attenuation. J. Colloid Interface Sci. 108, 442–450.Google Scholar
Keller, J. B. & Miksis, M. J. 1983 Surface tension driven flows. SIAM J. Appl. Maths 43, 268–277.Google Scholar
Krishnan, S., Hopfinger, E. J. & Puthenveettil, B. A. 2017 On the scaling of jetting from bubble collapse at a liquid surface. J. Fluid Mech. 822, 791–812.Google Scholar
Kumar, K. & Tuckerman, L. S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.Google Scholar
Lamb, H. 1932 Hydrodynamics, 6th edn. p. 738. Cambridge University Press.Google Scholar
Lighthill, J. 1978 Waves in Fluids, p. 504. Cambridge University Press.Google Scholar
Longuet-Higgins, M. S. 1983 Bubbles, breaking waves and hyperbolic jets at a free surface. J. Fluid Mech. 127, 103–121.Google Scholar
Longuet-Higgins, M. S. 1990 An analytic model of sound production by raindrops. J. Fluid Mech. 214, 395–410.Google Scholar
Longuet-Higgins, M. S. 2001 Vertical jets from standing waves. Proc. R. Soc. Lond. A 457, 495–510.Google Scholar
Longuet-Higgins, M. S. & Dommermuth, D. G. 2001 Vertical jets from standing waves. II. Proc. R. Soc. Lond. A 457, 2137–2149.Google Scholar
Longuet-Higgins, M. S. & Oguz, H. N. 1995 Critical microjets in collapsing cavities. J. Fluid Mech. 290, 183–201.Google Scholar
Longuet-Higgins, M. S. & Oguz, H. N. 1997 Critical jets in surface waves and collapsing cavities. Phil. Trans. R. Soc. Lond. A 355, 625–639.Google Scholar
Ludwig, C., Dreyer, M. E. & Hopfinger, E. J. 2013 Pressure variations in a cryogenic liquid storage tank subjected to periodic excitations. Intl J. Heat Mass Transfer 66, 223–234.Google Scholar
Miles, J. & Henderson, D. 1990 Parametrically forced surface waves. Annu. Rev. Fluid Mech. 22, 143–165.Google Scholar
Moran, M. E., McNelis, N. B., Kudlac, M. T., Haberbusch, M. S. & Satornino, G. A. 1994 Experimental results of hydrogen slosh in a 62 cubic foot (1750 liter) tank. 30th Joint Propulsion Conference. AIAA.Google Scholar
Rajan, G. K. & Henderson, D. M. 2018 Linear waves at a surfactant-contaminated interface separating two fluids: dispersion and dissipation of capillary-gravity waves. Phys. Fluids 30, 072104.Google Scholar
Zeff, B. W., Kleber, B., Fineberg, J. & Lathrop, D. P. 2000 Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 403, 401–404.Google Scholar