On symmetric intrusions in a linearly stratified ambient: a revisit of Benjamin's steady-state propagation results

Abstract

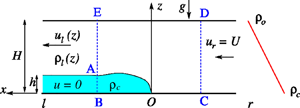
Previous studies have extended Benjamin's theory for an inertial steady-state gravity current of density $\rho _{c}$ in a homogeneous ambient fluid of density $\rho _{o} < \rho _{c}$ to the counterpart propagation in a linearly stratified (Boussinesq) ambient (density decreases from $\rho _b$ to $\rho _{o}$). The extension is typified by the parameter $S = (\rho _{b}-\rho _{o})/(\rho _{c}-\rho _{o}) \in (0,1]$, uses Long's solution for the flow over a topography to model the flow of the ambient over the gravity current, and reduces well to the classical theory for small and moderate values of $S$. However, for $S=1$, i.e. $\rho _b = \rho _c$, which corresponds to a symmetric intrusion, various idiosyncrasies appear. Here attention is focused on this case. The control-volume analysis (balance of volume, mass, momentum and vorticity) produces a fairly compact analytical formulation, pending a closure for the head loss, and subject to stability criteria (no inverse stratification downstream). However, we show that plausible closures that work well for the non-stratified current (like zero head loss on the stagnation line, or zero vorticity diffusion) do not produce satisfactory results for the intrusion (except for some small ranges of the height ratio of current to channel, $a = h/H$). The reasons and insights are discussed. Accurate data needed for comparison with the theoretical model are scarce, and a message of this paper is that dedicated experiments and simulations are needed for the clarification and improvement of the theory.