Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Marjanovic, Goran
Taub, Gordon
and
Balachandar, S.
2019.
On the effects of buoyancy on higher order moments in lazy plumes.
Journal of Turbulence,
Vol. 20,
Issue. 2,
p.
121.
Jiang, L.
Creyssels, M.
Hunt, G. R.
and
Salizzoni, P.
2019.
Control of light gas releases in ventilated tunnels.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
515.
Zheng, Yuan
Ye, Kai
Liu, Hong
Peng, Fei
Cao, Bei
Huang, Yubiao
and
Yang, Lizhong
2020.
Research on the plume shape under optimal wind environment to prevent the smoke backflow and combustion gains in utility tunnel.
Fire and Materials,
Vol. 44,
Issue. 1,
p.
139.
Ciriello, F.
and
Hunt, G. R.
2020.
Analytical solutions and virtual origin corrections for forced, pure and lazy turbulent plumes based on a universal entrainment function.
Journal of Fluid Mechanics,
Vol. 893,
Issue. ,
Li, Shuo
and
Flynn, M.R.
2021.
Coaxial plumes: Theory and experiment.
International Journal of Heat and Mass Transfer,
Vol. 174,
Issue. ,
p.
121311.
Dai, Yuchen
Klimenko, Alexander
Lu, Yuanshen
and
Hooman, Kamel
2021.
Asymptotic approximations for swirling turbulent plume rising from circular sources.
Physical Review Fluids,
Vol. 6,
Issue. 9,
Chu, Chi-Ming
2021.
Cold Inflow-Free Solar Chimney.
p.
75.
Mei, Shuo-Jun
and
Yuan, Chao
2021.
Three-dimensional simulation of building thermal plumes merging in calm conditions: Turbulence model evaluation and turbulence structure analysis.
Building and Environment,
Vol. 203,
Issue. ,
p.
108097.
Vraciu, Cristian V.
2022.
On the energy–consistent plume model in the convective boundary layer.
Dynamics of Atmospheres and Oceans,
Vol. 100,
Issue. ,
p.
101330.
Bilyaz, Serhat
and
Ezekoye, Ofodike A.
2022.
Modeling the dispersion and mixing of light gases in enclosed spaces using the Method of Moments.
Journal of Loss Prevention in the Process Industries,
Vol. 80,
Issue. ,
p.
104877.
Schellenberg, Louis M.
Newton, Thomas J.
and
Hunt, Gary R.
2023.
On the rotation of melting ice disks.
Environmental Fluid Mechanics,
Vol. 23,
Issue. 2,
p.
465.
Webb, Jamie P.
Wise, Nick H.
and
Hunt, Gary R.
2023.
Turbulent plumes above a heated plate.
Journal of Fluid Mechanics,
Vol. 959,
Issue. ,
Huang, Shanjie
Wang, Lingxue
Hu, Xu
Yuan, Shouzhang
Xu, Fangyu
Zhao, Jinsong
and
Cai, Yi
2023.
Study of transient behaviors of wavefront error caused by natural convection for improving mirror seeing.
Optics Express,
Vol. 31,
Issue. 11,
p.
17148.
Garvey, R. S.
and
Fowler, A. C.
2023.
On the mathematical theory of plumes.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 117,
Issue. 2,
p.
79.
Richards, Megan K.
Coker, Oluwaseun E.
Florido, Jose
Nicholls, Rhiannon A.M.
Ross, Andrew N.
and
Rooney, Gabriel G.
2023.
On the near-field interaction of vertically offset turbulent plumes.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Salizzoni, Pietro
Peruzzi, Cosimo
Marro, Massimo
Cingi, Pietro
Angeli, Diego
Kubwimana, Thierry
and
Mos, Antoine
2023.
Measurements and scaling of buoyancy-induced flows in ventilated tunnels.
Flow,
Vol. 3,
Issue. ,
Meehan, Michael A.
and
Hamlington, Peter E.
2023.
Richardson and Reynolds number effects on the near field of buoyant plumes: flow statistics and fluxes.
Journal of Fluid Mechanics,
Vol. 961,
Issue. ,
Taha, Mostafa
Zhao, Song
Lamorlette, Aymeric
Consalvi, Jean-Louis
and
Boivin, Pierre
2024.
Large eddy simulation of fire-induced flows using Lattice-Boltzmann methods.
International Journal of Thermal Sciences,
Vol. 197,
Issue. ,
p.
108801.
Hassanzadeh, H.
and
Taghavi, S. M.
2024.
A review on free miscible buoyant jets.
Physics of Fluids,
Vol. 36,
Issue. 6,
Zúñiga, Santiago L.
Balachandar, S.
Yang, Y.
Zhang, Y.
Smith, K.
Loppi, N.
Cantero, M. I.
and
Kerkemeier, S.
2024.
Planar wall plumes bounded by vertical and inclined surfaces.
Physics of Fluids,
Vol. 36,
Issue. 3,
 $\unicode[STIX]{x1D6E4}$, is used to characterize plumes and jets. The far-field behaviour of these flows has been studied in great detail while the near-field behaviour has not quite received the same attention. We examine near-field phenomena such as radial constriction, termed necking, and vortex structure formations with new high resolution direct numerical simulations. Four lazy plumes with increasing values of the source plume parameter,
$\unicode[STIX]{x1D6E4}$, is used to characterize plumes and jets. The far-field behaviour of these flows has been studied in great detail while the near-field behaviour has not quite received the same attention. We examine near-field phenomena such as radial constriction, termed necking, and vortex structure formations with new high resolution direct numerical simulations. Four lazy plumes with increasing values of the source plume parameter, 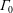 $\unicode[STIX]{x1D6E4}_{0}$, are simulated. We study the evolution of entrainment and the plume function. The original assumptions, that Reynolds stresses dominate viscous shear stresses, do not hold for lazy plumes in the near field. Due to this, a deviation from self-similarity occurs initially and is corrected by a large entrainment coefficient caused by vortex stretching and compression. After correcting for the virtual origin, comparison between theory and simulations shows a monotonic decay of
$\unicode[STIX]{x1D6E4}_{0}$, are simulated. We study the evolution of entrainment and the plume function. The original assumptions, that Reynolds stresses dominate viscous shear stresses, do not hold for lazy plumes in the near field. Due to this, a deviation from self-similarity occurs initially and is corrected by a large entrainment coefficient caused by vortex stretching and compression. After correcting for the virtual origin, comparison between theory and simulations shows a monotonic decay of 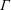 $\unicode[STIX]{x1D6E4}$ towards pure plume behaviour. The entrainment coefficient asymptotes to a widely accepted constant value for plumes.
$\unicode[STIX]{x1D6E4}$ towards pure plume behaviour. The entrainment coefficient asymptotes to a widely accepted constant value for plumes.