Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chiarini, Alessandro
Gatti, Davide
Cimarelli, Andrea
and
Quadrio, Maurizio
2022.
Structure of turbulence in the flow around a rectangular cylinder.
Journal of Fluid Mechanics,
Vol. 946,
Issue. ,
Chiarini, Alessandro
Quadrio, Maurizio
and
Auteri, Franco
2022.
An almost subharmonic instability in the flow past rectangular cylinders.
Journal of Fluid Mechanics,
Vol. 950,
Issue. ,
Fang, Xingjun
Tachie, Mark F.
and
Dow, Karen
2022.
Turbulent separations beneath semi-submerged bluff bodies with smooth and rough undersurfaces.
Journal of Fluid Mechanics,
Vol. 947,
Issue. ,
Chiarini, A.
Quadrio, M.
and
Auteri, F.
2022.
A new scaling for the flow instability past symmetric bluff bodies.
Journal of Fluid Mechanics,
Vol. 936,
Issue. ,
Chiarini, Alessandro
and
Auteri, Franco
2023.
Linear global and asymptotic stability analysis of the flow past rectangular cylinders moving along a wall.
Journal of Fluid Mechanics,
Vol. 966,
Issue. ,
Wu, Jian
Liu, Yakun
Zhang, Di
Cao, Ze
and
Li, Zhuoyue
2023.
Numerical simulation of vortex shedding from rectangular cylinders with different elongation ratios.
Fluid Dynamics Research,
Vol. 55,
Issue. 1,
p.
015503.
Liu, Junle
Tse, K. T.
Hu, Gang
Liu, Chang
Zhang, Bingchao
and
Kwok, Kenny C. S.
2024.
Exploring aerodynamics of a rectangular cylinder using flow field and surface pressure synchronized testing technique.
Physics of Fluids,
Vol. 36,
Issue. 8,
Li, Jiang-Hua
Wang, Bo-Fu
Qiu, Xiang
Zhou, Quan
Fu, Shi-Xiao
and
Liu, Yu-Lu
2024.
Vortex dynamics and boundary layer transition in flow around a rectangular cylinder with different aspect ratios at medium Reynolds number.
Journal of Fluid Mechanics,
Vol. 982,
Issue. ,
Liu, Junle
Shum, Kihing
Tse, Tim K. T.
and
Hu, Gang
2024.
Bidirectional prediction between wake velocity and surface pressure using deep learning techniques.
Physics of Fluids,
Vol. 36,
Issue. 2,
Li, Jiang-hua
Wang, Bo-fu
Qiu, Xiang
Zhou, Quan
Fu, Shi-xiao
and
Liu, Yu-lu
2024.
Turbulent transports in the flow around a rectangular cylinder with different aspect ratios.
Ocean Engineering,
Vol. 301,
Issue. ,
p.
117512.
Muniyammal, Ragavendiran
Gopalakrishnan, Shyam Sunder
Kumar, Sanjay
and
Mandal, Alakesh Chandra
2024.
Fluid Mechanics and Fluid Power, Volume 7.
p.
257.
Li, Jiang-Hua
Wang, Bo-Fu
Qiu, Xiang
Zhou, Quan
Fu, Shi-Xiao
and
Liu, Yu-Lu
2025.
Vortex dynamics and turbulence transport in flow around a near-wall rectangular cylinder.
Physics of Fluids,
Vol. 37,
Issue. 3,
Lin, Shuaihang
Meng, Hao
Yang, Wenhan
and
Gao, Donglai
2025.
Experimental investigation on the aerodynamics and flow patterns of a 5:1 rectangular cylinder with spoilers.
Experimental Thermal and Fluid Science,
Vol. 160,
Issue. ,
p.
111284.
Chiarini, Alessandro
and
Nastro, Gabriele
2025.
Wake transition and aerodynamics of a dragonfly-inspired airfoil.
Journal of Fluid Mechanics,
Vol. 1009,
Issue. ,
Liu, Junle
Tse, K.T.
and
Hu, Gang
2025.
An aerodynamic database of synchronized surface pressure and flow field for 2D rectangular cylinders.
Engineering Structures,
Vol. 326,
Issue. ,
p.
119506.
Li, Jiang-Hua
Wang, Bo-Fu
Qiu, Xiang
Zhou, Quan
Fu, Shi-Xiao
and
Liu, Yu-Lu
2025.
Near-wall effect on vortex dynamics in the flow around a rectangular cylinder.
Journal of Fluid Mechanics,
Vol. 1011,
Issue. ,
Zhu, Hongyu
Dong, Haotian
and
Du, Xiaoqing
2025.
Reynolds number effects on the flow around a 4:1 rectangular cylinder.
International Journal of Mechanical Sciences,
Vol. 301,
Issue. ,
p.
110541.
Chiarini, Alessandro
and
Boujo, Edouard
2025.
Stability and dynamics of the laminar flow past rectangular prisms.
Journal of Fluid Mechanics,
Vol. 1008,
Issue. ,
Derakhshandeh, Javad Farrokhi
2025.
Impact of length ratio on vibration frequencies and localized stress in flexible cylindrical shells: A comprehensive fluid structure interaction analysis.
Physics of Fluids,
Vol. 37,
Issue. 1,
Wan, Jiawei
Cai, Yunzhu
and
Fang, Hai
2025.
An experimental study of aerodynamics on cable-supported photovoltaic panel arrays at different tilt angles.
Journal of Wind Engineering and Industrial Aerodynamics,
Vol. 262,
Issue. ,
p.
106093.
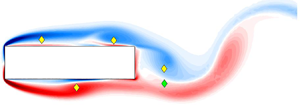
 $Re=400$, i.e. when locking is strong. Several two-dimensional, nonlinear simulations are run for rectangular and D-shaped cylinders, with the aspect ratio ranging from
$Re=400$, i.e. when locking is strong. Several two-dimensional, nonlinear simulations are run for rectangular and D-shaped cylinders, with the aspect ratio ranging from  $1$ to
$1$ to  $11$, and a global linear stability analysis of the flow is performed. The shedding frequency observed in the nonlinear simulations is predicted fairly well by the eigenfrequency of the leading eigenmode. The inspection of the structural sensitivity confirms the central role of the trailing-edge vortex shedding in the frequency locking, as already assumed by other authors. Surprisingly, however, the stepwise increase of the Strouhal number with the aspect ratio reported by several previous works is not fully reproduced. Indeed, with increasing aspect ratio, two distinct flow behaviours are observed, associated with two flow configurations where the interaction between the leading- and trailing-edge vortices is different. These two configurations are fully characterised, and the mechanism of selection of the flow configuration is discussed. Lastly, for aspect ratios close to the jump between two consecutive shedding modes, the Strouhal number is found to present hysteresis, implying the existence of multiple stable configurations. Continuing the lower shedding-mode branch by increasing the aspect ratio, we found that the periodic configuration loses stability via a Neimark–Sacker bifurcation leading to different Arnold tongues. This hysteresis can explain, at least partially, the significant scatter of existing experimental and numerical data.
$11$, and a global linear stability analysis of the flow is performed. The shedding frequency observed in the nonlinear simulations is predicted fairly well by the eigenfrequency of the leading eigenmode. The inspection of the structural sensitivity confirms the central role of the trailing-edge vortex shedding in the frequency locking, as already assumed by other authors. Surprisingly, however, the stepwise increase of the Strouhal number with the aspect ratio reported by several previous works is not fully reproduced. Indeed, with increasing aspect ratio, two distinct flow behaviours are observed, associated with two flow configurations where the interaction between the leading- and trailing-edge vortices is different. These two configurations are fully characterised, and the mechanism of selection of the flow configuration is discussed. Lastly, for aspect ratios close to the jump between two consecutive shedding modes, the Strouhal number is found to present hysteresis, implying the existence of multiple stable configurations. Continuing the lower shedding-mode branch by increasing the aspect ratio, we found that the periodic configuration loses stability via a Neimark–Sacker bifurcation leading to different Arnold tongues. This hysteresis can explain, at least partially, the significant scatter of existing experimental and numerical data.