Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Onorato, Miguel
and
Suret, Pierre
2016.
Twenty years of progresses in oceanic rogue waves: the role played by weakly nonlinear models.
Natural Hazards,
Vol. 84,
Issue. S2,
p.
541.
Janssen, Peter A. E. M.
2016.
Rogue and Shock Waves in Nonlinear Dispersive Media.
Vol. 926,
Issue. ,
p.
117.
Toffoli, Alessandro
2016.
Rogue and Shock Waves in Nonlinear Dispersive Media.
Vol. 926,
Issue. ,
p.
179.
Ducrozet, Guillaume
Bonnefoy, Félicien
Le Touzé, David
and
Ferrant, Pierre
2016.
HOS-ocean: Open-source solver for nonlinear waves in open ocean based on High-Order Spectral method.
Computer Physics Communications,
Vol. 203,
Issue. ,
p.
245.
Fedele, Francesco
2016.
Are Rogue Waves Really Unexpected?.
Journal of Physical Oceanography,
Vol. 46,
Issue. 5,
p.
1495.
Fedele, Francesco
Brennan, Joseph
Ponce de León, Sonia
Dudley, John
and
Dias, Frédéric
2016.
Real world ocean rogue waves explained without the modulational instability.
Scientific Reports,
Vol. 6,
Issue. 1,
Benetazzo, Alvise
Ardhuin, Fabrice
Bergamasco, Filippo
Cavaleri, Luigi
Guimarães, Pedro Veras
Schwendeman, Michael
Sclavo, Mauro
Thomson, Jim
and
Torsello, Andrea
2017.
On the shape and likelihood of oceanic rogue waves.
Scientific Reports,
Vol. 7,
Issue. 1,
Fedele, Francesco
Lugni, Claudio
and
Chawla, Arun
2017.
The sinking of the El Faro: predicting real world rogue waves during Hurricane Joaquin.
Scientific Reports,
Vol. 7,
Issue. 1,
Donelan, Mark A.
and
Magnusson, Anne-Karin
2017.
The Making of the Andrea Wave and other Rogues.
Scientific Reports,
Vol. 7,
Issue. 1,
Rao, Ji-Guang
Liu, Yao-Bin
Qian, Chao
and
He, Jing-Song
2017.
Rogue Waves and Hybrid Solutions of the Boussinesq Equation.
Zeitschrift für Naturforschung A,
Vol. 72,
Issue. 4,
p.
307.
Ducrozet, Guillaume
and
Gouin, Maïté
2017.
Influence of varying bathymetry in rogue wave occurrence within unidirectional and directional sea-states.
Journal of Ocean Engineering and Marine Energy,
Vol. 3,
Issue. 4,
p.
309.
Rao, Jiguang
Porsezian, Kuppuswamy
and
He, Jingsong
2017.
Semi-rational solutions of the third-type Davey-Stewartson equation.
Chaos: An Interdisciplinary Journal of Nonlinear Science,
Vol. 27,
Issue. 8,
Janssen, Peter A. E. M.
and
Janssen, Augustus J. E. M.
2019.
Asymptotics for the long-time evolution of kurtosis of narrow-band ocean waves.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
790.
Fedele, Francesco
Herterich, James
Tayfun, Aziz
and
Dias, Frederic
2019.
Large nearshore storm waves off the Irish coast.
Scientific Reports,
Vol. 9,
Issue. 1,
Dudley, John M.
Genty, Goëry
Mussot, Arnaud
Chabchoub, Amin
and
Dias, Frédéric
2019.
Rogue waves and analogies in optics and oceanography.
Nature Reviews Physics,
Vol. 1,
Issue. 11,
p.
675.
Fujimoto, Wataru
Waseda, Takuji
and
Webb, Adrean
2019.
Impact of the four-wave quasi-resonance on freak wave shapes in the ocean.
Ocean Dynamics,
Vol. 69,
Issue. 1,
p.
101.
Zhang, H.D.
Shi, H.D.
and
Soares, C. Guedes
2019.
Evolutionary properties of mechanically generated deepwater extreme waves induced by nonlinear wave focusing.
Ocean Engineering,
Vol. 186,
Issue. ,
p.
106077.
Jiang, Xingjie
Guan, Changlong
and
Wang, Daolong
2019.
Rogue waves during Typhoon Trami in the East China Sea.
Journal of Oceanology and Limnology,
Vol. 37,
Issue. 6,
p.
1817.
Eeltink, D.
Armaroli, A.
Ducimetière, Y. M.
Kasparian, J.
and
Brunetti, M.
2019.
Single-spectrum prediction of kurtosis of water waves in a nonconservative model.
Physical Review E,
Vol. 100,
Issue. 1,
Fedele, Francesco
Banner, Michael L.
and
Barthelemy, Xavier
2020.
Crest speeds of unsteady surface water waves.
Journal of Fluid Mechanics,
Vol. 899,
Issue. ,
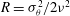 $R={\it\sigma}_{{\it\theta}}^{2}/2{\it\nu}^{2}$, a measure of short-crestedness for the dominant waves, with
$R={\it\sigma}_{{\it\theta}}^{2}/2{\it\nu}^{2}$, a measure of short-crestedness for the dominant waves, with  ${\it\nu}$ and
${\it\nu}$ and 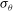 ${\it\sigma}_{{\it\theta}}$ denoting spectral bandwidth and angular spreading. Our refinement leads to a new analytical solution for the dynamic kurtosis of narrowband directional waves described with a Gaussian-type spectrum. For multidirectional or short-crested seas initially homogeneous and Gaussian, in a focusing (defocusing) regime dynamic kurtosis grows initially, attaining a positive maximum (negative minimum) at the intrinsic time scale
${\it\sigma}_{{\it\theta}}$ denoting spectral bandwidth and angular spreading. Our refinement leads to a new analytical solution for the dynamic kurtosis of narrowband directional waves described with a Gaussian-type spectrum. For multidirectional or short-crested seas initially homogeneous and Gaussian, in a focusing (defocusing) regime dynamic kurtosis grows initially, attaining a positive maximum (negative minimum) at the intrinsic time scale 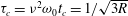 ${\it\tau}_{c}={\it\nu}^{2}{\it\omega}_{0}t_{c}=1/\sqrt{3R}$, or
${\it\tau}_{c}={\it\nu}^{2}{\it\omega}_{0}t_{c}=1/\sqrt{3R}$, or 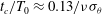 $t_{c}/T_{0}\approx 0.13/{\it\nu}{\it\sigma}_{{\it\theta}}$, where
$t_{c}/T_{0}\approx 0.13/{\it\nu}{\it\sigma}_{{\it\theta}}$, where 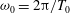 ${\it\omega}_{0}=2{\rm\pi}/T_{0}$ denotes the dominant angular frequency. Eventually the dynamic excess kurtosis tends monotonically to zero as the wave field reaches a quasi-equilibrium state characterized by nonlinearities mainly due to bound harmonics. Quasi-resonant interactions are dominant only in unidirectional or long-crested seas where the longer-time dynamic kurtosis can be larger than that induced by bound harmonics, especially as the Benjamin–Feir index increases. Finally, we discuss the implication of these results for the prediction of rogue waves.
${\it\omega}_{0}=2{\rm\pi}/T_{0}$ denotes the dominant angular frequency. Eventually the dynamic excess kurtosis tends monotonically to zero as the wave field reaches a quasi-equilibrium state characterized by nonlinearities mainly due to bound harmonics. Quasi-resonant interactions are dominant only in unidirectional or long-crested seas where the longer-time dynamic kurtosis can be larger than that induced by bound harmonics, especially as the Benjamin–Feir index increases. Finally, we discuss the implication of these results for the prediction of rogue waves.


