Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T06:40:48.227Z Has data issue: false hasContentIssue false
  • English
  • Français

On the laminar–turbulent transition of the rotating-disk flow: the role of absolute instability

Published online by Cambridge University Press:  17 March 2014

Shintaro Imayama ,
P. Henrik Alfredsson  and
R. J. Lingwood
Shintaro Imayama
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
P. Henrik Alfredsson
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden
R. J. Lingwood*
Affiliation:
Linné Flow Centre, KTH Mechanics, SE-100 44 Stockholm, Sweden Institute of Continuing Education, University of Cambridge, Madingley Hall, Madingley, Cambridge CB23 8AQ, UK
*
†Email address for correspondence: lingwood@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper describes a detailed experimental study using hot-wire anemometry of the laminar–turbulent transition region of a rotating-disk boundary-layer flow without any imposed excitation of the boundary layer. The measured data are separated into stationary and unsteady disturbance fields in order to elaborate on the roles that the stationary and the travelling modes have in the transition process. We show the onset of nonlinearity consistently at Reynolds numbers, 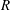$R$, of $\sim $510, i.e. at the onset of Lingwood’s (J. Fluid Mech., vol. 299, 1995, pp. 17–33) local absolute instability, and the growth of stationary vortices saturates at a Reynolds number of 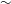$\sim $550. The nonlinear saturation and subsequent turbulent breakdown of individual stationary vortices independently of their amplitudes, which vary azimuthally, seem to be determined by well-defined Reynolds numbers. We identify unstable travelling disturbances in our power spectra, which continue to grow, saturating at around 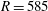$R=585$, whereupon turbulent breakdown of the boundary layer ensues. The nonlinear saturation amplitude of the total disturbance field is approximately constant for all considered cases, i.e. different rotation rates and edge Reynolds numbers. We also identify a travelling secondary instability. Our results suggest that it is the travelling disturbances that are fundamentally important to the transition to turbulence for a clean disk, rather than the stationary vortices. Here, the results appear to show a primary nonlinear steep-fronted (travelling) global mode at the boundary between the local convectively and absolutely unstable regions, which develops nonlinearly interacting with the stationary vortices and which saturates and is unstable to a secondary instability. This leads to a rapid transition to turbulence outward of the primary front from approximately 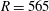$R=565$ to 590 and to a fully turbulent boundary layer above 650.

JFM classification

Instability: Absolute/convective instability Boundary Layers: Boundary layer stability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 745 , 25 April 2014 , pp. 132 - 163
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balachandar, S., Streett, C. L. & Malik, M. R. 1992 Secondary instability in rotating-disk flow. J. Fluid Mech. 242, 323–347.CrossRefGoogle Scholar
Cham, T.-S. & Head, M. R. 1969 Turbulent boundary-layer flow on a rotating disk. J. Fluid Mech. 37, 129–147.CrossRefGoogle Scholar
Chernoray, V. G., Dovgal, A. V., Kozlov, V. V. & Löfdahl, L. 2005 Experiments on secondary instability of streamwise vortices in a swept-wing boundary layer. J. Fluid Mech. 534, 295–325.Google Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37, 357–392.Google Scholar
Corke, T. C. & Knasiak, K. F. 1998 Stationary travelling cross-flow mode interactions on a rotating disk. J. Fluid Mech. 355, 285–315.Google Scholar
Dagenhart, J. R. & Saric, W. S.1999 Cross-flow stability and transition experiments in swept-wing flow NASA/TP-1999-209344.Google Scholar
Davies, C. & Carpenter, P. W. 2003 Global behaviour corresponding to the absolute instability of the rotating-disc boundary layer. J. Fluid Mech. 486, 287–329.CrossRefGoogle Scholar
Faller, A. J. 1991 Instability and transition of disturbed flow over a rotating disk. J. Fluid Mech. 230, 245.CrossRefGoogle Scholar
Garrett, S. J., Harris, J. & Thomas, P. J. 2012 On the effect of distributed roughness on transition over rotor-stator devices. In Proc. 28th ICAS Cong. 2012, Brisbane, Australia (ed. Grant, I.), pp. 1–8.Google Scholar
Gregory, N., Stuart, J. T. & Walker, W. S. 1955 On the stability of three-dimensional boundary layers with application to the flow due to a rotating disk. Phil. Trans. R. Soc. Lond. 248, 155–199.Google Scholar
Harris, J., Garrett, S. J. & Thomas, P. J.2012 On the stability of flows over rough rotating disks AIAA Paper 2012-3075, pp. 1–11.Google Scholar
Healey, J. J. 2010 Model for unstable global modes in the rotating-disk boundary layer. J. Fluid Mech. 663, 148–159.CrossRefGoogle Scholar
Hussain, Z., Garrett, S. J. & Stephen, S. O. 2011 The instability of the boundary layer over a disk rotating in an enforced axial flow. Phys. Fluids 23, 114108.CrossRefGoogle Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J.2011 An experimental study of laminar-turbulent transition of a rotating-disk flow In EUROMECH Colloquium 525, Instabilities and Transition in Three-Dimensional Flows with Rotation, Écully, France, pp. 29–30.Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2012 A new way to describe the transition characteristics of a rotating-disk boundary-layer flow. Phys. Fluids 24, 031701.Google Scholar
Imayama, S., Alfredsson, P. H. & Lingwood, R. J. 2013 An experimental study of edge effects on rotating-disk transition. J. Fluid Mech. 716, 638–657.Google Scholar
Imayama, S., Lingwood, R. J. & Alfredsson, P. H. 2014 An experimental study of a rotating-disk turbulent boundary-layer flow. In Proc. Phys.–iTi Conference on Turbulence (ed. Talamelli, A., Oberlack, M. & Peinke, J.), vol. 149, pp. 173–176. Springer.Google Scholar
Jarre, S., Le Gal, P. & Chauve, M. P. 1996 Experimental study of rotating disk instability. I. Natural flow. Phys. Fluids 8, 496–508.Google Scholar
von Kármán, T. 1921 Über laminare und turbulente Reibung. Z. Angew. Math. Mech. 1, 233–252.CrossRefGoogle Scholar
Kawakami, M., Kohama, Y. & Okutsu, M.1999 Stability characteristics of stationary cross-flow vortices in three-dimensional boundary layer. AIAA Paper 99-0811.Google Scholar
Kobayashi, R., Kohama, Y. & Takamadate, C. 1980 Spiral vortices in boundary layer transition regime on a rotating disk. Acta Mechanica 35, 71–82.Google Scholar
Kohama, Y. 1984 Study on boundary layer transition of a rotating disk. Acta Mechanica 50, 193–199.CrossRefGoogle Scholar
Kohama, Y., Suda, K. & Watanabe, H. 1994 Traveling disturbances on a spinning disk boundary layer. Trans. JSME B 60 (574), 1978–1984.CrossRefGoogle Scholar
Le Gal, P. 1992 Complex demodulation applied to the transition to turbulence of the flow over a rotating disk. Phys. Fluids A 4, 2523–2528.Google Scholar
Lingwood, R. J. 1995 Absolute instability of the boundary layer on a rotating disk. J. Fluid Mech. 299, 17–33.Google Scholar
Lingwood, R. J. 1996 An experimental study of absolute instability of the rotating-disk boundary-layer flow. J. Fluid Mech. 314, 373–405.Google Scholar
Lingwood, R. J. 1997a Absolute instability of the Ekman layer and related rotating flows. J. Fluid Mech. 331, 405–428.Google Scholar
Lingwood, R. J. 1997b On the impulse response for swept boundary-layer flows. J. Fluid Mech. 344, 317–334.CrossRefGoogle Scholar
Lingwood, R. J. & Garrett, S. J. 2011 The effects of surface mass flux on the instability of the BEK system of rotating boundary-layer flows. Eur. J. Mech. (B/Fluids) 30, 299–310.CrossRefGoogle Scholar
Malik, M. R., Wilkinson, S. P. & Orszag, S. A. 1981 Instability and transition in rotating disk flow. AIAA J. 19, 1131–1138.Google Scholar
Othman, H. & Corke, T. C. 2006 Experimental investigation of absolute instability of a rotating-disk boundary layer. J. Fluid Mech. 565, 63–94.Google Scholar
Pier, B. 2003 Finite-amplitude cross-flow vortices, secondary instability and transition in the rotating-disk boundary layer. J. Fluid Mech. 487, 315–343.CrossRefGoogle Scholar
Pier, B. & Huerre, P. 2001 Nonlinear self-sustained structures and fronts in spatially developing wake flows. J. Fluid Mech. 435, 145–174.Google Scholar
Siddiqui, M. E., Mukund, V., Scott, J. & Pier, B. 2013 Experimental characterization of transition region in rotating-disk boundary layer. Phys. Fluids 25, 034102.Google Scholar
Smith, N. H.1947 Exploratory investigation of laminar-boundary-layer oscillations on a rotating disk. NACA TN 1227.Google Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2008 The elephant mode between two rotating disks. J. Fluid Mech. 598, 451–464.CrossRefGoogle Scholar
Viaud, B., Serre, E. & Chomaz, J.-M. 2011 Transition to turbulence through steep global-modes cascade in an open rotating cavity. J. Fluid Mech. 688, 493–506.Google Scholar
Wilkinson, S. P. & Malik, M. R. 1985 Stability experiments in the flow over a rotating disk. AIAA J. 23, 588–595.CrossRefGoogle Scholar