Published online by Cambridge University Press: 13 September 2016
We present an experimental study of the time evolution of an isolated anticyclonic pancake vortex in a laboratory rotating stratified flow. Motivations come from the variety of compact anticyclones observed to form and persist for a strikingly long lifetime in geophysical and astrophysical settings combining rotation and stratification. We generate anticyclones by injecting a small amount of isodense fluid at the centre of a rotating tank filled with salty water linearly stratified in density. The velocity field is measured by particle image velocimetry in the vortex equatorial plane. Our two control parameters are the Coriolis parameter 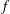 $f$ and the Brunt–Väisälä frequency
$f$ and the Brunt–Väisälä frequency 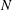 $N$. We observe that anticyclones always slowly decay by viscous diffusion, spreading mainly in the horizontal direction irrespective of the initial aspect ratio. This behaviour is correctly explained by a linear analytical model in the limit of small Rossby and Ekman numbers, where density and velocity equations reduce to a single equation for the pressure. In particular for
$N$. We observe that anticyclones always slowly decay by viscous diffusion, spreading mainly in the horizontal direction irrespective of the initial aspect ratio. This behaviour is correctly explained by a linear analytical model in the limit of small Rossby and Ekman numbers, where density and velocity equations reduce to a single equation for the pressure. In particular for 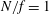 $N/f=1$, this equation ultimately simplifies to a radial diffusion equation, which admits an analytical self-similar solution. Direct numerical simulations further confirm the theoretical predictions that are not accessible to laboratory measurements. Notably, they show that the azimuthal shear stress generates secondary circulations, which advect the density anomaly: this mechanism is responsible for the slow time evolution, rather than the classical viscous dissipation of the azimuthal kinetic energy. The importance of density diffusivity is also analysed, showing that the product of the Schmidt and Burger numbers – rather than the bare Schmidt number – quantifies the importance of salt diffusion. Finally, a brief application to oceanic Meddies is considered.
$N/f=1$, this equation ultimately simplifies to a radial diffusion equation, which admits an analytical self-similar solution. Direct numerical simulations further confirm the theoretical predictions that are not accessible to laboratory measurements. Notably, they show that the azimuthal shear stress generates secondary circulations, which advect the density anomaly: this mechanism is responsible for the slow time evolution, rather than the classical viscous dissipation of the azimuthal kinetic energy. The importance of density diffusivity is also analysed, showing that the product of the Schmidt and Burger numbers – rather than the bare Schmidt number – quantifies the importance of salt diffusion. Finally, a brief application to oceanic Meddies is considered.