Article contents
On the mechanism of turbulent drag reduction with super-hydrophobic surfaces
Published online by Cambridge University Press: 22 May 2015
Abstract
The mechanism of turbulent drag reduction (DR) with super-hydrophobic (SH) surfaces is investigated by direct numerical simulation (DNS) and analysis of the governing equations in channel flow. The DNS studies were performed using lattice Boltzmann methods in channels with ‘idealized’ SH surfaces on both walls, comprised of longitudinal micro-grooves (MG), transverse MG, or micro-posts. DRs of 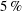 $5\,\%$ to
$5\,\%$ to 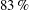 $83\,\%$,
$83\,\%$, 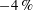 $-4\,\%$ to
$-4\,\%$ to 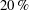 $20\,\%$, and
$20\,\%$, and 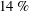 $14\,\%$ to
$14\,\%$ to 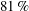 $81\,\%$ were realized in DNS with longitudinal MG, transverse MG, and micro-posts, respectively. By mathematical analysis of the governing equations, it is shown that, in SH channel flows with any periodic SH micro-pattern on the walls, the magnitude of DR can be expressed as
$81\,\%$ were realized in DNS with longitudinal MG, transverse MG, and micro-posts, respectively. By mathematical analysis of the governing equations, it is shown that, in SH channel flows with any periodic SH micro-pattern on the walls, the magnitude of DR can be expressed as 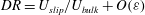 $DR=U_{slip}/U_{bulk}+O({\it\varepsilon})$, where the first term represents the DR resulting from the effective slip on the walls, and the second term represents the DR or drag increase (DI) resulting from modifications to the turbulence dynamics and any secondary mean flows established in the SH channel compared to a channel flow with no-slip walls at the same bulk Reynolds number as the SH channel. Comparison of this expression to DNS results shows that, with all SH surface micro-patterns studied, between 80 % and 100 % of the DR in turbulent flow arises from the effective slip on the walls. Modifications to the turbulence dynamics contribute no more than 20 % of the total DR with longitudinal MG or micro-posts of high shear-free fraction (SFF), and a DI with transverse MG or micro-posts of moderate SFF. The effect of the SH surface on the normalized dynamics of turbulence is found to be small in all cases, and confined to additional production of turbulence kinetic energy (TKE) within a thin ‘surface layer’ of thickness of the order of the width of surface micro-indentations. Outside of this ‘surface layer’, the normalized dynamics of turbulence proceeds as in a turbulent channel flow with no-slip walls at the friction Reynolds number of the SH channel flow.
$DR=U_{slip}/U_{bulk}+O({\it\varepsilon})$, where the first term represents the DR resulting from the effective slip on the walls, and the second term represents the DR or drag increase (DI) resulting from modifications to the turbulence dynamics and any secondary mean flows established in the SH channel compared to a channel flow with no-slip walls at the same bulk Reynolds number as the SH channel. Comparison of this expression to DNS results shows that, with all SH surface micro-patterns studied, between 80 % and 100 % of the DR in turbulent flow arises from the effective slip on the walls. Modifications to the turbulence dynamics contribute no more than 20 % of the total DR with longitudinal MG or micro-posts of high shear-free fraction (SFF), and a DI with transverse MG or micro-posts of moderate SFF. The effect of the SH surface on the normalized dynamics of turbulence is found to be small in all cases, and confined to additional production of turbulence kinetic energy (TKE) within a thin ‘surface layer’ of thickness of the order of the width of surface micro-indentations. Outside of this ‘surface layer’, the normalized dynamics of turbulence proceeds as in a turbulent channel flow with no-slip walls at the friction Reynolds number of the SH channel flow.
- Type
- Rapids
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 104
- Cited by



