On the modelling of the transition between contact-line and microlayer evaporation regimes in nucleate boiling

Abstract

Formation of a microlayer in nucleate boiling results in substantial changes to the heat-transfer dynamics of the process, and establishing a criterion to distinguish between the microlayer and contact-line regimes encountered is necessary to obtain a quantitative description of the nucleate-boiling phenomenon. In this work, we describe microlayer formation as a dewetting transition in the presence of phase change. We derive a specific criterion for modelling the transition based on a synthesis of existing theoretical, experimental and numerical data. As a result, a new formulation of the transition criterion is developed, and applied to (i) reference data from a dewetting experiment of a volatile liquid, and (ii) results derived from a high-resolution direct numerical simulation of nucleate boiling. In both cases, very good agreement is found for Jakob numbers $\lesssim$75, a range which covers many important boiling situations.

1. Introduction

Nucleate-boiling heat transfer is one of the most efficient modes of heat transfer under high heat-flux conditions, and it is used in many engineering applications, such as refrigeration, cooling systems, boilers and heat exchangers. Although there are a multitude of applications, identification of the principal mechanisms driving the heat-transfer process still remains an area of active research. One of the main uncertainties is the role of microlayer formation and evaporation in the overall dynamics, as well as its relationship to the occurrence of departure from nucleate boiling.

The microlayer, presumed to be located at the base of a growing bubble on a horizontal, hot surface, as shown schematically in figure 1, is a layer of liquid with thickness less than a few micrometres, and has been observed to form beneath vapour bubbles during nucleate boiling under certain conditions (Kim 2009). The microlayer extends from the liquid bulk up to the so-called contact-line region (also referred to as the microregion, and labelled as such in the figure), where vapour and liquid meet on the hot surface; this is followed by a dry patch (Kim 2009). The dry patch is sometimes assumed to be covered by an adsorbed film of molecular thickness, presenting no resistance to heat transfer (Schweikert, Sielaff & Stephan 2019). Recent numerical evidence (Hänsch & Walker 2016; Guion et al. 2018; Urbano et al. 2018) suggests that the microlayer profile is not of monotonic shape, but rather features a thickened region, or ‘hump’, immediately adjacent to the microregion (see inset to figure 1). Such a profile, i.e. a thin liquid film on a solid wall terminated by a hump, can also be observed during adiabatic dewetting of partially wetting fluids (Snoeijer et al. 2007; Delon et al. 2008).

Figure 1. Schematic visualisation of the microlayer located at the base if a growing bubble during nucleate boiling. Inset (top right) illustrates the termination of the microlayer by a ‘hump’.

After its formation, the microlayer appears to begin to evaporate rapidly, contributing significantly to the overall heat-transfer mechanism (Yabuki & Nakabeppu 2017). While the reported contribution of microlayer evaporation to the overall bubble growth is still disputed in the literature (Kim 2009), more recent measurements indicate contributions of 15 %–50 % to the growth, depending on the fluid chosen and the exact experimental conditions (Yabuki & Nakabeppu 2014; Utaka et al. 2018), with locally measured heat-flux values in the microlayer reaching $1\ \textrm {MW}\ \textrm {m}^{-2}$ (Yabuki & Nakabeppu 2014). This suggests that the microlayer dynamics is of considerable importance in the nucleate-boiling process.

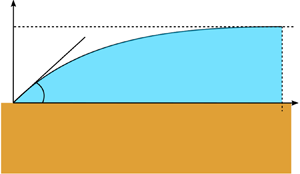
The actual presence of a microlayer during nucleate boiling is not always guaranteed: for example, if the bubble growth is sufficiently slow, a microlayer is not always observed, and then the overall bubble shape remains essentially spherical (Son, Dhir & Ramanujapu 1999; Fischer et al. 2014; Huber et al. 2017; Urbano et al. 2018). In this so-called contact-line regime, the liquid bulk surrounding the bubble is sharply terminated by the presence of a dry patch, as shown in figure 2. Note that the absence of a microlayer significantly reduces the overall heat transfer.

Figure 2. Schematic visualisation of the contact-line nucleate-boiling regime.

As the transition between the contact-line regime of boiling and boiling in the presence of a microlayer (microlayer evaporation regime) results in qualitative changes in the overall dynamics, identifying the conditions under which microlayer formation takes place is crucial for a full understanding of the nucleate-boiling heat-transfer process. Conceptually, growth of a bubble on a solid surface during nucleate boiling represents an example of dewetting in the presence of phase change. Problems involving adiabatic dewetting are well known to feature qualitative regime transitions associated with a certain critical velocity: e.g. droplets undergo a shape transition if they are sliding ‘too quickly’ along a surface (Le Grand, Daerr & Limat 2005), and a liquid film, known as the Landau–Levich film (Levich & Landau 1942), is known to adhere to a plate if it is withdrawn from a liquid bath sufficiently fast.

The hypothesis that the microlayer formation mechanism could be understood in terms of a dewetting transition in the presence of phase change has been discussed frequently in the past (more recently by Afkhami et al. 2018; Guion et al. 2018). Also, Schweikert et al. (2019) performed the plate-withdrawal experiment for a volatile liquid in order to understand the transition between the contact-line and microlayer evaporation regimes: they observed the occurrence of a wetting transition qualitatively similar to that of the adiabatic case (i.e. the Landau–Levich transition). Furthermore, Urbano et al. (2018) simulated numerically microlayer formation during nucleate boiling using direct numerical simulation (DNS), and suggested that a microlayer would be formed if the radial bubble expansion velocity exceeded a certain critical value, which the authors estimated from a fit to the DNS data they obtained.

In view of the available evidence, we support the hypothesis of microlayer formation based on dewetting. Furthermore, we believe that it is possible to quantify the threshold criterion between the contact-line evaporation regime and the microlayer evaporation regime. Consequently, in this work, we propose a correlation for this transition based on the Cox–Voinov law for volatile liquids in § 2, which we then validate in § 3 using the experimental data of Schweikert et al. (2019). In § 4, we extend the application of the criterion to nucleate boiling and compare results to the DNS data of Urbano et al. (2018). We discuss also, in general terms, the relative benefits and limitations of DNS investigations of microlayer dynamics. Furthermore, we speculate on the initial microlayer thickness following its formation. Finally, overall conclusions are drawn in § 5. Additionally, appendix A details results of our own simulations of microlayer formation that we have performed to support the arguments developed in the paper.

2. Criterion formulation

In the context of dynamic, adiabatic wetting phenomena, analytic solutions of quasi-static, contact-line motion have resulted in constitutive laws being proposed connecting an apparent contact angle $\theta _{app}$ (the macroscopically observed interfacial slope) with the microscopic contact angle $\theta _0$ (described below) and the capillary number $Ca$ (Snoeijer et al. 2007; Bonn et al. 2009), viz

(2.1)\begin{equation} \theta_{app} = f(Ca,\theta_0). \end{equation}

The capillary number is given as

(2.2)\begin{equation} Ca = \frac{\mu_l U_{CL}}{\sigma}, \end{equation}

with $U_{CL}$ being the contact-line velocity along the surface ($\textrm {m}\ \textrm {s}^{-1}$), $\sigma$ the surface tension ($\textrm {N}\ \textrm {m}^{-1}$) and $\mu _l$ the liquid dynamic viscosity ($\textrm {Pa}\ \textrm {s}$). The microscopic contact angle is conventionally assumed to be constant (i.e. any hysteresis effects are neglected), and to result from a force balance at the triple line (Snoeijer et al. 2007). A prominent example of (2.1) is the Cox–Voinov law, written with the dewetting sign convection (Voinov 1976; Cox 1986) as

(2.3)\begin{equation} \theta_0^3-\theta_{app}^3 = \frac{\textit{Ca}}{A}. \end{equation}

This law has been shown to represent measured experimental data in a variety of configurations: for example in droplet sliding (Le Grand et al. 2005), spreading (Kant et al. 2017) and spreading with solidification (de Ruiter et al. 2017). The constant $A$ is unknown a priori and is usually determined by a fit to experimental data. Equation (2.3) was also found to hold in the presence of liquid-to-vapour phase change by Janeček & Nikolayev (2013) from a numerical solution of the lubrication equations, coupled with steady-state one-dimensional heat conduction. However, in this context, the equation takes the form (Fourgeaud et al. 2016)

(2.4)\begin{equation} \theta_{mr}^3(\Delta T,\textit{Ca}=0)-\theta_{app}^3 = \frac{\textit{Ca}}{A}, \end{equation}

where $\theta _{mr}(\Delta T,{Ca}=0)$ is the static contact angle for the volatile liquid under non-isothermal conditions, which takes into account the effect of phase change in the microregion on the interfacial slope. We will denote this quantity by the symbol $\theta _{mr}$ and, for brevity, refer to it as the non-adiabatic contact angle. The actual value of $\theta _{mr}$ can be non-zero, even for fully wetting liquids (Raj et al. 2012; Fourgeaud et al. 2016; Schweikert et al. 2019). Note that (2.4) essentially states that the effect of phase change ($\Delta T$) and contact-line motion (Ca) on the apparent contact angle can be decoupled (Janeček & Nikolayev 2013; Fourgeaud et al. 2016).

A wetting transition as $\theta _{app}\rightarrow 0$ has already been conjectured by Derjaguin & Levi (1964), analytically derived by Eggers (2005) and numerically confirmed by Snoeijer et al. (2007). Note that, in this last paper, it was shown that, at the transition point, the solutions undergo a series of saddle-node bifurcations, featuring a non-monotonically shaped film, and asymptotically tending to an infinitely long flat film behind the contact line. Under the condition $\theta _{app}=0$, (2.4) immediately gives, at the transition

(2.5)\begin{equation} \theta_{mr}^3 = \frac{{Ca}}{A}. \end{equation}

Rearranging, and using (2.2), we obtain a corresponding relation for the critical contact-line velocity as

(2.6)\begin{equation} U_{CL,{crit}}=\frac{\sigma}{\mu_l}A\theta_{mr}^3, \end{equation}

and we identify the condition $U_{CL}\geqslant U_{CL,{crit}}$ with liquid-film (i.e. microlayer) formation due to dewetting transition.

For the value of $A$, results of sliding droplet experiments suggest a value of $A\approx 4.5\times 10^{-3}$ for water (Podgorski, Flesselles & Limat 2001; Winkels et al. 2011). This value is considered to be anomalously low, and possibly reflective of the occurrence of non-hydrodynamic dissipative mechanisms near the contact line (de Ruiter et al. 2017). For sliding droplets, constituted by a silicone oil–water mixture, a value of $A\approx 10^{-2}$ has been proposed (Podgorski et al. 2001; Le Grand et al. 2005; Winkels et al. 2011), essentially independently of the degree of oil–water mixing. Generally, the choice of $A$ remains a source of uncertainty in (2.6), as it is a parameter dependent on properties of the test fluid, surface characteristics, solid–fluid interactions as well as on the particular geometry of the configuration. At the same time, theoretical predictions from the original Cox–Voinov law give (Bonn et al. 2009)

(2.7)\begin{equation} A =\frac{1}{9\ln (S)}= \frac{1}{9\ln\left(l/a\right)}, \end{equation}

where $S$ is a ratio of two scales: $a$ is a representative nanoscopic length scale. Under adiabatic conditions, it can be taken to be the typical molecule size, of the order of 0.1–1 nm (Podgorski et al. 2001; Le Grand et al. 2005; Winkels et al. 2011), or the slip length, a typical value for very smooth surfaces being 10 nm (Janeček & Nikolayev 2013). In the context of microlayer formation, $a$ would be a typical scale of the microregion, of the order of 10–100 nm (Janeček 2012; Janeček & Nikolayev 2013; Fourgeaud et al. 2016), while $l$ represents a macroscopic dimension, dependent on the problem in question. The described configuration is summarised schematically in figure 3.

Figure 3. A visualisation of the film profile with a receding contact line. A dewetting transition occurs as the interfacial slope $\theta _{app}\rightarrow 0$ at $x=l$, since $U_{CL}\geqslant U_{CL,crit}$. The inset (left) shows schematically the effect of phase change on the interfacial slope in the microregion. Length scales $l$ and $a$ from (2.7) are indicated.

3. Application of the criterion to experimental data on plate dewetting

With their experiments, Schweikert et al. (2019) were able to produce a regime map of microlayer formation for the fluorocarbon FC-72 based on the values of the wall superheat $\Delta T$ (up to 5 K) and a critical plate withdrawal velocity of up to $45\ \textrm {mm}\ \textrm {s}^{-1}$ (figure 9 in their paper). We have deduced the transition criterion directly from this figure to be (the plate-withdrawal velocity corresponding to the contact-line velocity)

(3.1)\begin{equation} U_{CL,{crit}}^{Schweikert}\ [\textrm{m}\ \textrm{s}^{{-}1}] = 3.12\times10^{{-}3} \Delta T^{1.44}. \end{equation}

By equating the plate-withdrawal velocity with the contact-line velocity, we have assumed that the principal effect of superheat in this experiment was to change the non-adiabatic contact angle, presuming the impact of phase change on the contact-line velocity to be minor, as indicated by Fourgeaud et al. (2016). Therefore, to apply our criterion to these data, we converted the applied superheats ($\Delta T$) into $\theta _{mr}$ values. Although this could be done numerically with the help of a microregion model, such models do not generally predict the $\theta _{mr}=f(\Delta T)$ relationship accurately, as can be seen from the attempts by Raj et al. (2012) and Janeček & Nikolayev (2013), especially for values of the superheat corresponding to the experimental conditions considered here. At the same time, FC-72 is known to be a non-polar liquid, fully wetting on the majority of surfaces (Reed & Mudawar 1997; Raj et al. 2012; Schweikert et al. 2019), and thus $\theta _{mr}$ should be essentially independent of the surface material in question. Indeed, even if a microregion model had been used, the surface would be characterised only by the Hamaker constant (Israelachvili 2011; Raj et al. 2012), and the overall microregion model results would then be ‘very insensitive even to large variations of more than one order of magnitude’ of this constant (Raj et al. 2012), erasing any differences between the materials comprising these surfaces.

For this reason, we consider the experimental, non-adiabatic contact angle values for FC-72 originally measured for copper by Raj et al. (2012) to be also applicable to the experimental conditions of Schweikert et al. (2019), in spite of the difference in surface material (i.e. copper vs chromium, both found to be essentially perfectly wetted by FC-72 under adiabatic conditions by the respective authors). By using uncertainty-weighted, least-squares regression, together with a fit equation of the form

(3.2)\begin{equation} \theta_{mr} = C_0 \Delta T^{C_1}, \end{equation}

we recover the relation (see figure 4):

(3.3)\begin{equation} \theta_{mr,fit} \ [^{{\circ}}] = 9.37 \Delta T^{0.54}. \end{equation}

Evidently, much better agreement with experimental data has been achieved with our relation than with the microregion model-based solution given by Raj et al. (2012), namely

(3.4)\begin{equation} \theta_{mr}^{\textit{Raj}}\ [^{{\circ}}] = 17.4 \Delta T^{0.323}, \end{equation}

especially in the interval of interest here, $\Delta T\leqslant 5\ \textrm {K}$. In order to incorporate the effect of experimental uncertainties into our model, we also complement the best-estimate fit with two bounding predictions, obtained by performing unweighted least-squares regression on the data (i) reduced by one standard deviation ($\theta ^{low}_{{mr}}$) and (ii) increased by one standard deviation ($\theta ^{high}_{{mr}}$). The resulting fitted relations

(3.5)\begin{gather} \theta^{low}_{mr,fit} \ [^{{\circ}}] = 6.54 \Delta T^{0.65}, \end{gather}

(3.6)\begin{gather}\theta^{high}_{mr,fit} \ [^{{\circ}}] = 13.7 \Delta T^{0.42}, \end{gather}

are also shown in figure 4.

Figure 4. Experimentally measured values of the non-adiabatic contact angle of FC-72 on copper (Raj et al. 2012) compared with a best-fit correlation (3.3), two bounding fitted correlations (3.5) and (3.6) and the results of the microregion model of Raj et al. (2012), (3.4).

Introducing (3.3) into (3.1), we obtain

(3.7)\begin{equation} U_{CL,{crit}}^{Schweikert}\ [\textrm{m}\ \textrm{s}^{{-}1}] = 8.00\times10^{{-}6} \theta_{mr,fit}^{2.67}. \end{equation}

The power-law dependence is remarkably close to the cubic relation predicted by the Cox–Voinov law (2.6), a fact further illustrated in figure 5, which shows the experimental results of Schweikert et al. (2019) converted to $U_{CL,{crit}}-\theta _{mr}$ space via (3.3). Here, we have introduced a fit using (2.6), and a very good delineation of the two regions has thereby been achieved. As can be seen, some discrepancies persist for smaller values of $\theta _{mr}$, for which the conversion of wall superheat $\Delta T$ to $\theta _{mr}$ is the least precise (see figure 4); furthermore, any influence of heater surface material characteristics would be most significant for such small superheat values.

Figure 5. Experimental data on regime transition obtained by Schweikert et al. (2019), with superheat values converted to non-adiabatic contact angle values using (3.3), and compared to a fit according to (2.6).

From this fit, it is possible to deduce the (assumed constant) value of $A$ in (2.6) to be 0.031. Similarly, by considering the two bounding correlations (3.5) and (3.6) instead of (3.3), we have obtained $A_{low}$ as 0.059 and $A_{high}$ as 0.016. These values are within the range of the typical order of magnitude estimates of $A$, as discussed in § 2. Due to the logarithmic relation between $A$ and $S$ and large spread in $A$ caused by the uncertainties in the contact angle measurement of Raj et al. (2012), significance of any point estimate of the ratio of scales $S$ in (2.7) would be small and thus it is not reported here.

Based on the arguments given in this section, we consider our correlation, (2.6), to represent the experimentally observed regime transition of Schweikert et al. (2019) sufficiently well to be adopted in this study.

4. Extension of theory to nucleate boiling

In the case of nucleate boiling, the contact-line velocity is no longer an independent parameter, as it was in the case of plate withdrawal; instead, it is related to the macroscopic bubble expansion. Without the presence of a microlayer, bubbles are observed to remain essentially of the spherical-cap type during growth (Son et al. 1999; Fischer et al. 2014) and, therefore, in a first approximation

(4.1)\begin{equation} U_{CL}\approx\sin(\theta_{mr})U_{BG}, \end{equation}

in which $U_{BG}$ is the radial bubble expansion velocity and the prefactor $\sin (\theta _{mr})$ results from geometrical considerations (see figure 6). With reference to the figure and denoting $R(t)$ (m) as the bubble radius as a function of time $t$ (s), the radial contact-line position $R_{CL}$ can be expressed as

(4.2)\begin{equation} R_{CL}=R\sin(\theta_{mr}), \end{equation}

and its velocity on the surface as

(4.3)\begin{equation} U_{CL}=\frac{\text{d}R_{CL}}{\text{d}t}\approx\sin(\theta_{mr})\frac{\text{d}R}{\text{d}t}=\sin(\theta_{mr})U_{BG}. \end{equation}

Figure 6. Schematic representation of spherical-cap bubble growth.

As our goal is to compare our criterion to the results of incompressible DNS, we will consider bubble growth solely in the heat-transfer-limited regime (Faghri & Zhang 2006). The alternative limiting situation, i.e. growth in the inertial regime, is discussed in § 4.3. For bubbles growing in uniformly superheated liquids (valid also if the thickness of the thermal boundary layer is sufficiently large compared to the bubble radius), the bubble growth in the heat-transfer-limited regime is given by (Scriven 1959)

(4.4)\begin{equation} R(t) = 2B(\Delta T) \sqrt{\alpha_l t}, \end{equation}

in which $\alpha _l$ is the liquid thermal diffusivity ($\textrm {m}^{2}\ \textrm {s}^{-1}$),

(4.5)\begin{equation} \alpha_l=\frac{\lambda_l}{\rho_l C_{p,l}}, \end{equation}

where $\Delta T$ is the applied superheat (K), $\lambda _l$ the liquid thermal conductivity ($\textrm {W}\ \textrm {mK}^{-1}$), $\rho _l$ the liquid density ($\textrm {kg}\ \textrm {m}^{-3}$), $C_{p,l}$ the liquid specific isobaric heat capacity ($\textrm {J}\ \textrm {kg}\ \textrm {K}^{-1}$) and $B$ (–) is a growth constant, dependent on $\Delta T$. Equation (4.4) can be rearranged to eliminate the explicit dependence on time into the form

(4.6)\begin{equation} U_{BG}=\frac{\text{d}R}{\text{d}t}=2B^2\frac{\alpha_l}{R}. \end{equation}

Using this expression, we immediately recover the microlayer formation criterion for bubble growth in the heat-transfer-limited regime from the condition $U_{CL}\geqslant U_{CL,{crit}}$ as

(4.7)\begin{equation} \frac{\theta_{mr}^3}{\sin(\theta_{mr})} \leqslant \frac{2B^2}{A}\frac{\mu_l\alpha_l}{\sigma}\frac{1}{R} = 18 B^2 \ln (S)\frac{\mu_l\alpha_l}{\sigma}\frac{1}{R}, \end{equation}

with $A$ and $S$ represented according to (2.7). Although multiple (approximate) expressions exist for the growth constant $B$ (Fritz & Ende 1936; Forster & Zuber 1954; Plesset & Zwick 1954), the quadratic dependence on $B$ evidenced in (4.7) signifies that it must be evaluated carefully. For this reason, we utilise the full solution of Scriven (1959), in which $B$ can be obtained as a root of the expression

(4.8)\begin{align} \frac{\rho_l}{\rho_v}\frac{C_{p,l}\Delta T}{L+(C_{p,l}-C_{p,v})\Delta T} = 2B^2\int_{0}^1\exp\left[{-}B^2\left((1-s)^{{-}2}-2\left(1-\frac{\rho_v}{\rho_l}\right)s-1\right)\right]\textrm{d}s, \end{align}

where $\rho _v$ ($\textrm {kg}\ \textrm {m}^{-3}$) is the vapour density, $L$ the latent heat of vaporisation ($\textrm {J}\ \textrm {kg}^{-1}$) and $C_{p,v}$ ($\textrm {J}\ \textrm {kg}\ \textrm {K}^{-1}$) the vapour specific isobaric heat capacity. The applicability of Scriven's solution to bubble growth on a heat-transfer surface remains open to discussion, since the solution is based on the assumptions of an unbounded domain in a uniformly superheated liquid. Nevertheless, Cole & Shulman (1966) have pointed out that if the liquid surrounding the bubble is superheated to the temperature of the wall, this description of the bubble growth would still be justified. As we are considering here the initial stages of bubble growth, in which the bubble is much smaller than the thickness of the thermal boundary layer, the assumption of uniform superheat is considered to be acceptable. Note that, for water under atmospheric conditions, the growth constant $B$ calculated according to (4.8) is approximately equal to the Jakob number Ja (–) given as

(4.9)\begin{equation} \textit{Ja}=\frac{\rho_l C_{p,l}\Delta T}{\rho_v L}. \end{equation}

This is illustrated by the red line in figure 7.

Figure 7. Scriven growth constant, (4.8), and its normalised value as functions of the Jakob number for water under atmospheric conditions.

According to our criterion, (4.7), a strong (inverse) dependence on the bubble radius $R$ can be observed. By rearranging the equation in the form

(4.10)\begin{equation} R_{crit}\leqslant 18B^2\ln (S) \frac{\mu_l\alpha_l}{\sigma}\frac{\sin(\theta_{mr})}{\theta_{mr}^3}, \end{equation}

we can interpret the resulting relation as a definition of a maximal bubble radius for which interfacial deformation due to the mismatch between macroscopic expansion and contact-line dynamics may be observed. In a broader sense, (4.10) determines those bubble sizes for which hydrodynamic effects contribute to microlayer expansion, rather than to its destruction. In other words, the microlayer expands with bubble growth if $R \leqslant R_{crit}$, and contracts otherwise. Indeed, a microlayer formed during nucleate boiling results in strong deformation of the overall bubble shape (Chen, Haginiwa & Utaka 2017; Yabuki & Nakabeppu 2017), and the appearance of which indicates a significant departure from equilibrium. As such, the presence of a microlayer should be seen as a dynamic phenomenon with a variety of possible outcomes, ranging from its fully developed formation, usually observed in experiments, to the transitory occurrence of highly deformed vapour/liquid interfaces. We further discuss implications of (4.10) in appendix A.

4.1. Comparisons with reference DNS data

We are not aware of any comprehensive experimental study of microlayer formation which would have produced data similar to those of Schweikert et al. (2019) from their plate-withdrawal tests. However, the work of Urbano et al. (2018) includes a set of predictions generated using DNS, showcasing the ability of computational fluid dynamics (CFD) as a tool to study the influence of individual, physical parameters on complex processes such as nucleate boiling. The DNS solver used in their work has been rigorously verified, grid convergence studies have been performed and code predictions have been validated for a variety of phase-change configurations, including nucleate boiling (e.g. Huber et al. 2017; Urbano, Tanguy & Colin 2019). Thus, we consider the results of Urbano et al. (2018) to represent a trustworthy DNS database, against which we can compare our findings.

In their study, the referenced authors examined microlayer formation in water under atmospheric conditions for several variants of contact angle and degree of superheat. Table 1 lists important parameters used in their simulations, and figure 8 gives a comparison of their numerical results with their own best-fit correlation. The contact angle, measured in degrees, is expressed in this correlation as follows:

(4.11)\begin{equation} \left(\frac{\theta_{mr}-5^\circ}{313}\right)^3 \leqslant \frac{\mu_l\alpha_l}{\sigma}\frac{\textit{Ja}^2}{\delta_{KS}}, \end{equation}

where $\delta _{KS}$ (m) is the Kays–Crawford free convection boundary layer thickness, given as (Kays, Crawford & Weigand 2003)

(4.12)\begin{equation} \delta_{KS} = 7.14\left(\frac{\mu_l\alpha_l}{\rho_l g\beta_l \Delta T}\right)^{1/3}, \end{equation}

with $g=9.81\ \textrm {m}\ \textrm {s}^{-2}$ being the gravitational acceleration, and $\beta _l$ the isobaric liquid thermal expansion coefficient $(\textrm {K}^{-1})$. Figure 9 is a plot of $\delta _{KS}$ as a function of Jakob number for water under atmospheric conditions, for which $\beta _l=7.52\times 10^{-4}\ \textrm {K}^{-1}$.

Figure 8. Numerical results on the transition to the micro-layer regime by Urbano et al. (2018) compared with their best-fit correlation, (4.11), and to a fit according to our correlation, (4.7), with $B$ determined from (4.8) and $R=R_0$ from table 1.

Figure 9. Kays–Crawford boundary layer thickness, (4.12), as a function of Jakob number for water under atmospheric conditions.

Table 1. Parameters used in the DNS study of Urbano et al. (2018).

Figure 8 also presents a fit of the intermediate data points using (4.7). The intermediate regime was previously described by Urbano et al. (2018) in terms of the appearance of strong interfacial deformation. Based on the discussion of the implications of (4.10) above, and further expanded in appendix A, we conjecture that this corresponds to the situation in which microlayer formation occurs only briefly after the onset of bubble growth, but then fails to fully develop due to the slowing of the bubble expansion. According to this line of reasoning, it follows immediately that the radius $R$ in (4.7) should be identified with the lowest available radius: i.e. the initial bubble radius $R_0$.

Evidently, (4.7) captures the delineation between the regimes to very good accuracy for small and moderate Jakob numbers. The associated value of $\ln (S)$ in (2.7) is $\sim$2, corresponding to a ratio of scales $S\approx 7.2$. Since this is a ratio of macroscopic to nanoscopic scales, the numerical value might be considered extremely small, but this is not surprising considering that the numerical slip length in a CFD simulation (without any special treatment) is of the order of the grid spacing $\Delta x$ (Afkhami et al. 2018). In the simulations analysed here, $\Delta x= 0.5\ \mathrm {\mu }\textrm {m}$; the microlayer scale after the onset of bubble growth is $O(1\ \mathrm {\mu }\text {m})$ as shown in appendix A. Evidently, the ratio of scales adopted is consistent with these values.

4.2. Novel aspects of our analysis

Our microlayer formation criterion deduced above (4.7) has several important characteristics. Namely:

1. (i) Its derivation is based on physical arguments. As a result, we consider that it offers new insights into microlayer dynamics, and highlights the transient character of the phenomena resulting from the interplay of dynamic wetting and bubble expansion due to phase change.

2. (ii) The expressions for the bubble expansion velocity (4.6) and threshold condition (2.6) are based on concepts well established in the literature: i.e. the solution of Scriven (1959) and the conjecture of Derjaguin & Levi (1964).

3. (iii) The role of the initial liquid temperature distribution on microlayer formation in the heat-transfer-limited regime is clarified in terms of the heat-transfer characteristics of the process. Indeed, at the initial stage of bubble expansion, prior to (any possible) microlayer formation, heat transfer from the liquid to the bubble interface is the major contributor to phase change; this permits the approximation of the bubble growth rate by the formula for a bubble growing in a superheated liquid, (4.6), to be adopted. During this time period, the temperature boundary layer thickness is generally much thicker than the bubble radius (see figure 9), so this approximation is expected to remain valid even under conditions of non-constant liquid superheat. Indeed, the thickness of the boundary layer should therefore have only a negligible influence on the overall dynamics; nevertheless, its thinning would act as an impediment to microlayer formation, since the bubble expansion would then be diminished due to the associated reduction in the overall heat flux. In the (hypothetical) case of the boundary layer thickness being comparable to the bubble size, a correction would then need to be implemented. This could possibly follow along the lines of Cole & Shulman (1966), who introduced an ‘effective superheat’ into their bubble-growth correlations. Appendix A further illustrates the role of the initial liquid superheat on microlayer formation by comparing results of simulations for which the surrounding liquid is uniformly superheated against those obtained assuming the liquid to be initially at saturation.

4.3. Benefits and limitations of DNS investigations of microlayer dynamics

Based on the insights gained from the analysis above, some of the benefits and limitations of a DNS investigation of microlayer dynamics should be emphasised. Clearly, the ability to freely vary material properties and boundary conditions allows DNS practitioners to methodically investigate the governing parameter space. For example, in reality, the non-adiabatic contact angle $\theta _{mr}$ is also a function of the wall superheat rather than being an independent variable, further complicating any interpretation of the experimental data.

From our own simulations, presented in appendix A, we have shown that the choice of the initial bubble size strongly affects the absence or presence of bubble interfacial deformation, which in extreme cases can lead to microlayer formation. For this reason, we conjecture that the sensitivity of the overall results to the initial conditions must be carefully evaluated in DNS studies. Note that the role of initial bubble radius on the observed dynamics, prominently featured in (4.7), is possibly an artefact of the numerical method employed, which considers only the heat-transfer-limited growth from a prescribed initial size. In reality, bubble nuclei start to grow from an embryonic radius $R_e$, which can be estimated as (Forster & Zuber 1955)

(4.13)\begin{equation} R_e \approx \frac{2\sigma T_s}{L\rho_v\Delta T} = O(1\ \mathrm{\mu}\text{m}), \end{equation}

where $T_s$ is the saturation temperature (K). The initial growth then occurs in the inertial regime, rather than in the heat-transfer-limited regime and the bubble-growth velocity can be approximately deduced from the asymptotic solution of the Rayleigh equation for spherical bubble growth on a plane surface (Witze, Schrock & Chambre 1968; Mikic, Rohsenow & Griffith 1970)

(4.14)\begin{equation} U_{BG}= \frac{\text{d}R}{\text{d}t} \approx \sqrt{\frac{\rm \pi}{7}\frac{\rho_v L}{\rho_l}\frac{{\Delta} T}{T_{{s}}}}; \end{equation}

this expression is independent of the bubble radius. Based on the conventional analysis comparing the growth as determined by the formulae for the heat-transfer-limited and inertial regimes (Faghri & Zhang 2006) and taking water at atmospheric conditions with superheat 10 K as an example, the inertial limit could be considered to be valid up to radii of ${\sim }100\text {--}150\ \mathrm {\mu }\textrm {m}$. This is in the range of sizes for which the microlayer formation can already be observed. Thus, the microlayer formation criterion taking into account the inertial regime, is

(4.15)\begin{equation} \frac{\theta_{mr}^3}{\sin(\theta_{mr})} \leqslant 9\ln(S)\frac{\mu_l}{\sigma}\sqrt{\frac{\rm \pi}{7}\frac{\rho_v L}{\rho_l}\frac{{\Delta} T}{T_{{s}}}} .\end{equation}

Applicability of this criterion to experimental data and/or results of DNS solvers capable of simulating the inertial bubble-growth regime should be addressed in future work.

Furthermore, significant attention must be paid to the very high value of the numerical slip, artificially introduced into classical CFD simulations by the very nature of the solution algorithm (Afkhami et al. 2018), and its impact on any deduced microlayer-forming criterion (e.g. via (4.7)) cannot be neglected. In addition, as the numerical slip length is at least an order of magnitude larger than the physical one (Afkhami et al. 2018), motion of the contact line is artificially promoted in CFD simulations. This could explain why dewetting phenomena play a more prominent role in CFD simulations incorporating a resolved microlayer (Guion et al. 2018; Urbano et al. 2018; Hänsch & Walker 2019, this paper) than in related experimental studies. Indeed, the microlayer profile has often been described as monotonic in the vicinity of the contact line, and its destruction has been attributed to the physical process of evaporation in many experimental works on boiling in the microlayer regime (e.g. Yabuki & Nakabeppu 2014, 2017; Utaka et al. 2018; Chen et al. 2020), while the results of DNS often feature a hump-terminated microlayer (see figure 1), more typical of film dewetting, with hydrodynamic expulsion attributed to be the principal driving mechanism for microlayer destruction by Urbano et al. (2018). This result is more consistent with experiments on volatile liquid films, for which a hump-like profile and dewetting chiefly due to capillary effects with only a minor role of evaporation have been reported (Fourgeaud et al. 2016). It appears that experimentally observed dynamics of deposited volatile films and of the microlayer are not fully equivalent, especially in regard to the role of wetting; this discrepancy should be investigated in future work. Nevertheless, to capture the conditions occurring during boiling and limit the numerical slip effects, a more elaborate representation of the wetting phenomenon should be implemented into DNS codes; this will improve the transferability of DNS results on microlayer dynamics from numerical simulation to physical reality.

A straightforward example of such a model is a mesh-independent approach based on the theory of dynamic wetting proposed, for example, by Afkhami, Zaleski & Bussmann (2009), Afkhami et al. (2018) and Legendre & Maglio (2015). Using the Cox–Voinov theory as demonstration, we can demand that the resulting interfacial slope is consistently reproduced, independently of mesh refinement. That is,

(4.16)\begin{equation} \theta_{app}^3 = \theta_{mr}^3 + 9\textit{Ca}\ln\left(\frac{x}{a}\right) = \theta_{\varDelta}^3 + 9\textit{Ca}\ln\left(\frac{x}{\varDelta}\right), \end{equation}

where $\theta _{\varDelta }$ is the mesh-dependent numerical contact angle, $\varDelta$ is a length characterising the numerical slip, and the capillary number Ca is based on the contact-line velocity. We can rearrange (4.16) as

(4.17)\begin{equation} \theta_{\varDelta}^3 = \theta_{mr}^3 + 9\textit{Ca}\left[\ln\left(\frac{x}{a}\right)-\ln\left(\frac{x}{\varDelta}\right)\right], \end{equation}

and immediately recover that the numerical contact angle should be given as

(4.18)\begin{equation} \theta_\varDelta = \sqrt[3]{\theta_{mr}^3 + 9\textit{Ca}\ln\left(\frac{\varDelta}{a}\right)}. \end{equation}

An example of the impact of this approach on microlayer dynamics in a simulation is presented in appendix A.

4.4. Remarks on initial microlayer thickness

Although the characteristics of a developed microlayer after its formation are not the main focus of this paper, we briefly remark on the (assumed) microlayer initial thickness $d$: i.e. its thickness before evaporation takes place. The classical theory of Cooper & Lloyd (1969), recently re-analysed by Yabuki & Nakabeppu (2017) and Guion et al. (2018), predicts

(4.19)\begin{equation} d(t)\propto\sqrt{\nu_l t}, \end{equation}

where $\nu _l=\mu _l/\rho _l$ is the liquid kinematic viscosity ($\textrm {m}^2\ \textrm {s}^{-1}$) and $t$ is the time since the onset of bubble growth. This expression has been derived under the assumption of a heat-transfer-limited regime, in which the bubble radius $R\propto \sqrt {\alpha _l t}$ (Scriven 1959), and is assumed to be valid provided that the microlayer is sufficiently thin (Yabuki & Nakabeppu 2017). Using (4.4), we can recast the relation as

(4.20)\begin{equation} d(R)\propto\sqrt{Pr_l}R, \end{equation}

where $Pr_l=\nu _l/\alpha _l$ (–) is the liquid Prandtl number. Although this proportionality expression had been introduced already by van Stralen et al. (1975), it has not received much attention in the literature to date. In their (experimental) work, Utaka, Kashiwabara & Ozaki (2013) found that, for water and ethanol, respectively

(4.21)\begin{gather} d_w = 4.46\times 10^{{-}3} r_s \text{ for water} \end{gather}

(4.22)\begin{gather}d_e = 1.02\times 10^{{-}2} r_s \text{ for ethanol}, \end{gather}

in which $r_s$ is the radial distance from the incipient bubble site along the heater surface. In their study, the bubbles were observed to grow almost hemispherically, so $r_s\approx R$. The ratio of the two experimental expressions is constant

(4.23)\begin{equation} \frac{d_e}{d_w} \approx 2.29. \end{equation}

Analogously, on theoretical grounds, (4.20), applied to both fluids simultaneously, predicts, under the assumption of an equal bubble-growth constant $B$

(4.24)\begin{equation} \frac{d_e(R)}{d_w(R)} = \sqrt{\frac{Pr_e}{Pr_w}} = 2.18, \end{equation}

in which the numerical ratio has been evaluated using the respective properties at saturation taken from the NIST Chemistry WebBook (Lemmon, McLinden & Friend 2018). The similarity between the experimental and theoretical predictions of the ratio of the initial microlayer thicknesses for the two fluids is suggestive, and should motivate further research with different working fluids to determine whether (4.20) represents a general correlation, or is just coincidental. Provided that substantial evidence for the scaling of the initial microlayer thickness in terms of $\sqrt {Pr_l}$ can be found, this result could perhaps be used to improve semi-empirical models of microlayer thickness estimation used in CFD simulations of boiling phenomena without a resolved microlayer, in the cases in which suitable correlations for the fluid in question are not available.

5. Conclusions

In this paper, we propose a rigorously derived correlation for predicting the transition between the contact-line regime and the microlayer evaporation regime in nucleate boiling, assuming that microlayer formation under a growing bubble on a hot surface corresponds physically to a dewetting transition, occurring if the contact-line velocity is greater than a given critical value. The correlation proposed for this transition is based on the Cox–Voinov law under non-adiabatic conditions. With reference to the experimentally measured data on non-adiabatic wetting of the fluorocarbon FC-72 (currently used in many electronic cooling devices), we have applied our newly formulated criterion to an experiment featuring plate withdrawal from a volatile fluid, and have achieved very good agreement with experimental data.

We have then extended the criterion to nucleate boiling by introducing a relation for the radial bubble-growth velocity in the heat-transfer-limited regime, and compared results to detailed DNS data. The agreement has again been shown to be very good for Jakob numbers $\lesssim$75, a range which covers many important industrial boiling situations, and we have supported our arguments with our own DNS data. Based on this analysis, we have discussed the relative benefits and limitations of DNS modelling of microlayer dynamics, and have identified the main drawbacks to be the inability of standard incompressible DNS solvers to capture the inertial growth regime and the artificially large value of the numerical slip length occurring when employing standard wetting models compared to the physical slip length. We have also highlighted the possible connection between this artificial slip and the observed discrepancies between DNS predictions and experimental data.

Finally, we have speculated on the role of the molecular Prandtl number on the scaling of the microlayer initial thickness for different liquids, which could prove useful in the development of semi-empirical computational microlayer models.

We recommend that future experimental work on the subject should concentrate on gathering more high-resolution data on the wetting of volatile liquids, since the study here suggests that the non-adiabatic contact angle plays a crucial role in the microlayer dynamics, and hence in the overall heat-transfer dynamics. Furthermore, an experimental database on microlayer formation during nucleate boiling should be developed, perhaps by varying the system pressure or the temperature for the onset of bubble nucleation. In terms of development of CFD techniques for resolved microlayer simulations, our work indicates that more advanced wetting models, aimed at reliably representing the contact-line dynamics (in particular by eliminating the effects of numerical slip), should be incorporated into DNS codes used for the modelling of these phenomena; furthermore, DNS solvers capable of simulating the inertial growth regime should be employed.