Article contents
On the nonlinear destabilization of stably stratified shear flow
Published online by Cambridge University Press: 15 August 2013
Abstract
A weakly nonlinear analysis of the bifurcation of the stratified Ekman boundary-layer flow near a critical bulk Richardson number is conducted and compared to a similar analysis of a continuously stratified parallel shear flow subject to Kelvin–Helmholtz instability. Previous work based on asymptotic expansions and predicting supercritical bifurcation at Prandtl number 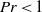 $Pr\lt 1$ and subcritical bifurcation at
$Pr\lt 1$ and subcritical bifurcation at  $Pr\gt 1$ for the parallel base flow is confirmed numerically and through fully nonlinear temporal simulations. When applied to the non-parallel Ekman flow, weakly nonlinear analysis and fully nonlinear calculations confirm that the nature of the bifurcation is dominantly controlled by
$Pr\gt 1$ for the parallel base flow is confirmed numerically and through fully nonlinear temporal simulations. When applied to the non-parallel Ekman flow, weakly nonlinear analysis and fully nonlinear calculations confirm that the nature of the bifurcation is dominantly controlled by 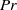 $Pr$, although a sharp threshold at
$Pr$, although a sharp threshold at 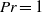 $Pr= 1$ is not found. In both flows the underlying physical mechanism is that the mean flow adjusts so as to induce a viscous (respectively diffusive) flux of momentum (respectively buoyancy) that balances the vertical flux induced by the developing instability, leading to a weakening of the mean shear and mean stratification. The competition between the former nonlinear feedback, which tends to be stabilizing, and the latter, which is destabilizing and strongly amplified as
$Pr= 1$ is not found. In both flows the underlying physical mechanism is that the mean flow adjusts so as to induce a viscous (respectively diffusive) flux of momentum (respectively buoyancy) that balances the vertical flux induced by the developing instability, leading to a weakening of the mean shear and mean stratification. The competition between the former nonlinear feedback, which tends to be stabilizing, and the latter, which is destabilizing and strongly amplified as 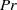 $Pr$ increases, determines the supercritical or subcritical character of the bifurcation. That essentially the same competition is at play in both the parallel shear flow and the Ekman flow suggests that the underlying mechanism is valid for complex, non-parallel stratified shear flows.
$Pr$ increases, determines the supercritical or subcritical character of the bifurcation. That essentially the same competition is at play in both the parallel shear flow and the Ekman flow suggests that the underlying mechanism is valid for complex, non-parallel stratified shear flows.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 3
- Cited by


