Published online by Cambridge University Press: 04 July 2023
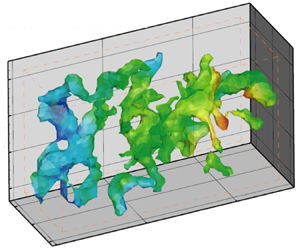
Cavitation inception in the turbulent shear layer developing behind a backward-facing step occurs at multiple points along quasi-streamwise vortices (QSVs), at a rate that increases with the Reynolds number (Re). This study investigates the evolution of the unsteady pressure field and the distribution of nuclei within and around the QSVs. The time-resolved volumetric velocity in the non-cavitating flow is measured using tomographic particle tracking, and the pressure is determined by spatial integration of the material acceleration. Analysis in Eulerian and Lagrangian reference frames reveals that the pressure is lower, and its minima last longer within the QSVs compared with the surrounding flow. The intermittent low pressure regions, whose sizes and shapes are consistent with those of the cavities, are likely to be preceded by axial vortex stretching and followed by contraction. Such phenomena have been observed before in simulations of stretched vortex elements. For the same axial straining, the pressure minima last longer with increasing Re, a trend elucidated in terms of viscous diffusion of the stretched vortex core. The impact of nuclei availability is studied under ‘natural’ and controlled seeding. Owing to differences in the saturation level of non-condensable gas, the microbubble concentration in the shear layer decreases with increasing Re, in contrast to the rate of cavitation events. Minor differences in entrainment rate into the shear layer also do not explain the substantial Re effects on cavitation inception. Hence, the Re scaling of inception appears to be dominated by trends of the pressure field.