Article contents
On the propagation of acoustic–gravity waves under elastic ice sheets
Published online by Cambridge University Press: 05 January 2018
Abstract
The propagation of wave disturbances in water of varying depth bounded above by ice sheets is discussed, accounting for gravity, compressibility and elasticity effects. Considering the more realistic scenario of elastic ice sheets reveals a continuous spectrum of acoustic–gravity modes that propagate even below the cutoff frequency of the rigid surface solution where surface (gravity) waves cannot exist. The balance between gravitational forces and oscillations in the ice sheet defines a new dimensionless quantity 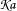 $\mathfrak{Ka}$. When the ice sheet is relatively thin and the prescribed frequency is relatively low (
$\mathfrak{Ka}$. When the ice sheet is relatively thin and the prescribed frequency is relatively low (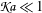 $\mathfrak{Ka}\ll 1$), the free-surface bottom-pressure solution is retrieved in full. However, thicker ice sheets or propagation of relatively higher frequency modes (
$\mathfrak{Ka}\ll 1$), the free-surface bottom-pressure solution is retrieved in full. However, thicker ice sheets or propagation of relatively higher frequency modes (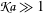 $\mathfrak{Ka}\gg 1$) alter the solution fundamentally, which is reflected in an amplified asymmetric signature and different characteristics of the eigenvalues, such that the bottom pressure is amplified when acoustic–gravity waves are transmitted to shallower waters. To analyse these scenarios, an analytical solution and a depth-integrated equation are derived for the cases of constant and varying depths, respectively. Together, these are capable of modelling realistic ocean geometries and an inhomogeneous distribution of ice sheets.
$\mathfrak{Ka}\gg 1$) alter the solution fundamentally, which is reflected in an amplified asymmetric signature and different characteristics of the eigenvalues, such that the bottom pressure is amplified when acoustic–gravity waves are transmitted to shallower waters. To analyse these scenarios, an analytical solution and a depth-integrated equation are derived for the cases of constant and varying depths, respectively. Together, these are capable of modelling realistic ocean geometries and an inhomogeneous distribution of ice sheets.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 16
- Cited by


