Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T13:28:37.645Z Has data issue: false hasContentIssue false
  • English
  • Français

On the scaling of air layer drag reduction

Published online by Cambridge University Press:  01 February 2013

Brian R. Elbing ,
Simo Mäkiharju ,
Andrew Wiggins ,
Marc Perlin ,
David R. Dowling  and
Steven L. Ceccio
Brian R. Elbing*
Affiliation:
Applied Research Laboratory, Pennsylvania State University, University Park, PA 16804, USA
Simo Mäkiharju
Affiliation:
Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Andrew Wiggins
Affiliation:
Naval Architecture and Marine Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Marc Perlin
Affiliation:
Naval Architecture and Marine Engineering, University of Michigan, Ann Arbor, MI 48109, USA
David R. Dowling
Affiliation:
Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA
Steven L. Ceccio
Affiliation:
Mechanical Engineering, University of Michigan, Ann Arbor, MI 48109, USA Naval Architecture and Marine Engineering, University of Michigan, Ann Arbor, MI 48109, USA
*
†Email address for correspondence: bre11@psu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Air-induced drag reduction was investigated on a 12.9 m long flat plate test model at a free stream speed of 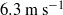$6. 3~\mathrm{m} ~{\mathrm{s} }^{- 1} $. Measurements of the local skin friction, phase velocity profiles (liquid and gas) and void fraction profiles were acquired at downstream distances to 11.5 m, which yielded downstream-distance-based Reynolds numbers above 80 million. Air was injected within the boundary layer behind a 13 mm backward facing step (BFS) while the incoming boundary layer was perturbed with vortex generators in various configurations immediately upstream of the BFS. Measurements confirmed that air layer drag reduction (ALDR) is sensitive to upstream disturbances, but a clean boundary layer separation line (i.e. the BFS) reduces such sensitivity. Empirical scaling of the experimental data was investigated for: (a) the critical air flux required to establish ALDR; (b) void fraction profiles; and (c) the interfacial velocity profiles. A scaling of the critical air flux for ALDR was developed from balancing shear-induced lift forces and buoyancy forces on a single bubble within a shear flow. The resulting scaling successfully collapses ALDR results from the current and past studies over a range of flow conditions and test model configurations. The interfacial velocity and void fraction profiles were acquired and scaled within the bubble drag reduction (BDR), ALDR and transitional ALDR regimes. The BDR interfacial velocity profile revealed that there was slip between phases. The ALDR results showed that the air layer thickness was nominally three-quarters of the total volumetric flux (per unit span) of air injected divided by the free stream speed. Furthermore, the air layer had an average void fraction of 0.75 and a velocity of approximately 0.2 times the free stream speed. Beyond the air layer was a bubbly mixture that scaled in a similar fashion to the BDR results. Transitional ALDR results indicate that this regime was comprised of intermittent generation and subsequent fragmentation of an air layer, with the resulting drag reduction determined by the fraction of time that an air layer was present.

JFM classification

Flow Control: Drag reduction
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 484 - 513
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amromin, E., Kopriva, J., Arndt, R. E. A. & Wosnik, M. 2006 Hydrofoil drag reduction by partial cavitation. Trans. ASME: J. Fluids Engng 128 (5), 931–936.Google Scholar
Bodgevich, V. G. & Evseev, A. R. 1976 The distribution of skin friction in a turbulent boundary layer of water beyond the location of gas injection. In Investigations of Boundary Layer Control, p. 62. Thermophysics Institute Publishing House (in Russian).Google Scholar
Brennen, C. E. 2005 Fundamentals of Multiphase Flow. Cambridge University Press.Google Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42, 183–203.CrossRefGoogle Scholar
Ceccio, S. L. & George, D. L. 1996 A review of electrical impedance techniques for the measurement of multiphase flows. J. Fluids Engng 118, 391–399.Google Scholar
Cho, J., Perlin, M. & Ceccio, S. L. 2005 Measurements of near-wall stratified bubbly flows using electrical impedance. Meas. Sci. Technol. 16 (4), 1021–1029.Google Scholar
Davis, A. M. J. & Lauga, E. 2010 Hydrodynamic friction of Fakir-like superhydrophobic surfaces. J. Fluid Mech. 661, 402–411.CrossRefGoogle Scholar
Druzhinin, O. A. & Elghobashi, S. 1998 Direct numerical simulations of bubble-laden turbulent flows using two-fluid formulation. Phys. Fluids 10, 685–697.Google Scholar
Elbing, B. R., Winkel, E. S., Lay, K. A., Ceccio, S. L., Dowling, D. R. & Perlin, M. 2008 Bubble-induced skin-friction drag reduction and the abrupt transition to air-layer drag reduction. J. Fluid Mech. 612, 201–236.Google Scholar
Elbing, B. R., Winkel, E. S., Ceccio, S. L., Perlin, M. & Dowling, D. R. 2010 High-Reynolds-number turbulent-boundary-layer wall pressure fluctuations with dilute polymer solutions. Phys. Fluids 22, 085104.Google Scholar
Elbing, B. R., Solomon, M. J., Perlin, M., Dowling, D. R. & Ceccio, S. L. 2011 Flow-induced degradation of drag-reducing polymer solutions within a high-Reynolds-number turbulent boundary layer. J. Fluid Mech. 670, 337–364.CrossRefGoogle Scholar
Etter, R. J., Cutbirth, J. M., Ceccio, S. L., Dowling, D. R. & Perlin, M. 2005 High Reynolds number experimentation in the U.S. Navy’s William B. Morgan large cavitation channel. Meas. Sci. Technol. 16 (9), 1701–1709.CrossRefGoogle Scholar
Ferrante, A. & Elghobashi, S. 2004 On the physical mechanisms of drag reduction in spatially developing turbulent boundary layer laden with microbubbles. J. Fluid Mech. 503, 345–355.CrossRefGoogle Scholar
Hewitt, G. F. 1978 Measurement of Two-Phase Flow Parameters. Academic.Google Scholar
Kim, J., Kline, S. J. & Johnston, J. P. 1980 Investigation of reattaching turbulent shear layer: flow over a backward-facing step. Trans. ASME: J. Fluid Engng 102, 302–308.Google Scholar
Klewicki, J. C. 2010 Reynolds number dependence, scaling, and dynamics of turbulent boundary layers. Trans. ASME: J. Fluids Engng 132 (9), 094001.Google Scholar
Kodama, Y., Kakugawa, A. & Takahashi, T. 1999 Preliminary experiments on microbubbles for drag reduction using a long flat plate ship, ONR Workshop on Gas Based Surface Ship Drag Reduction (Newport, USA), 1–4.Google Scholar
Kodama, Y., Kakugawa, A., Takahashi, T. & Kawashima, H. 2000 Experimental study on microbubbles and their applicability to ships for skin friction reduction. Intl J. Heat Fluid Flow 21, 582–588.CrossRefGoogle Scholar
Kodama, Y., Kakugawa, A., Takahashi, T., Nagaya, S. & Sugiyama, K. 2002 Microbubbles: drag reduction mechanism and applicability to ships, 24th Symposium on Naval Hydrodynamics, 1–19. The National Academies Press.Google Scholar
Kodama, Y., Hori, T., Kawashima, M. M. & Hinatsu, M. 2006 A full scale microbubble experiment using a cement carrier, European Drag Reduction and Flow Control Meeting, Ischia, Italy, 1–2.Google Scholar
Konrad, J. 2011 The bubble ship – Mitsubishi’s new green ship technology, gCaptain, Unofficial Networks, October 24, http://www.gcaptain.com.Google Scholar
Kundu, P. K., Cohen, I. M. & Dowling, D. R. 2012 Fluid Mechanics, 5th edn. pp. 236–240 Elsevier.Google Scholar
Lay, K. A., Yakushiji, R., Mäkiharju, S., Perlin, M. & Ceccio, S. L. 2010 Partial cavity drag reduction at high Reynolds numbers. J. Ship Res. 54 (2), 109–119.Google Scholar
Lee, C. & Kim, C. J. 2011 Underwater restoration and retention of gases on superhydrophobic surfaces for drag reduction. Phys. Rev. Lett. 106 (1), 014502.Google Scholar
Lu, J., Fernández, A. & Tryggvason, G. 2005 The effect of bubbles on the wall drag of a turbulent channel flow. Phys. Fluids 17, 095102.CrossRefGoogle Scholar
Lumley, J. L. 1973 Drag reduction in turbulent flow by polymer additives. J. Polym. Sci., Macromolecular Rev. 7, 283–290.CrossRefGoogle Scholar
Lumley, J. L. 1977 Drag reduction in two phase and polymer flows. Phys. Fluids 20, S64–S70.CrossRefGoogle Scholar
Madavan, N. K., Deutsch, S. & Merkle, C. L. 1985 Measurements of local skin friction in a microbubble modified turbulent boundary layer. J. Fluid Mech. 156, 237–256.CrossRefGoogle Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32, 659–708.CrossRefGoogle Scholar
Mäkiharju, S. 2012 The dynamics of ventilated partial cavities over a wide range of Reynolds numbers and quantitative 2D X-ray densitometry for multiphase flow, PhD thesis, University of Michigan.Google Scholar
Martell, M. B., Perot, J. B. & Rothstein, J. P. 2009 Direct numerical simulations of turbulent flows over superhydrophobic surfaces. J. Fluid Mech. 620, 31–41.CrossRefGoogle Scholar
Matveev, K. I., Burnett, T. J. & Ockfen, A. E. 2009 Study of air-ventilated cavity under model hull on water surface. Ocean Engng 36 (12–13), 930–940.CrossRefGoogle Scholar
Matveev, K. I. & Miller, M. J. 2011 Air cavity with variable length under a model hull. Proc. IMechE M: J. Engng Maritime Environ. 225, 161–169.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a non-uniform flow. Phys. Fluids 26, 883–889.CrossRefGoogle Scholar
McCormick, M. E. & Battacharyya, R. 1973 Drag reduction of a submersible hull by electrolysis. Naval Engrs J. 85, 11–16.Google Scholar
Meng, J. C. S. & Uhlman, J. S. 1998 Microbubble formation and splitting in a turbulent boundary layer for turbulence reduction, Proceedings of the International Symposium on Seawater Drag Reduction, 341–355.Google Scholar
Merkle, C. & Deutsch, S. 1990 Drag reduction in liquid boundary layers by gas injection. In Viscous Drag Reduction in Boundary Layers (ed. Bushnell, D. M. & Hefner, J. N.), Progress in Astronautics and Aeronautics , 123. pp. 351–412. AIAA.Google Scholar
Merkle, C. & Deutsch, S. 1992 Microbubble drag reduction in liquid turbulent boundary layers. Appl. Mech. Rev. 45 (3), 103–127.Google Scholar
Nagamatsu, T., Kodama, T., Kakugawa, A., Takai, M., Murakami, K., Ishikawa, H., Kamiirisa, S., Ogiwara, Y., Yoshida, T., Suzuki, Y., Toda, H., Kato, A., Ikemoto, S., Yamatani, S., Imo, K. & Yamashita, 2002 A full-scale experiment on microbubbles for skin friction reduction using SEIUN MARU. Part 2. The full-scale experiment. J. Soc. Nav. Archit. Japan 192, 15–28.Google Scholar
Nagaya, S., Kakugawa, A., Kodama, Y. & Hishida, K. 2001 PIV/LIF measurements on 2-D turbulent channel flow with microbubbles, 4th International Symposium on PIV, Goettingen, Germany.Google Scholar
Oweis, G. F., Winkel, E. S., Cutbrith, J. M., Ceccio, S. L., Perlin, M. & Dowling, D. R. 2010 The mean velocity profile of a smooth-flat-plate turbulent boundary layer at high Reynolds number. J. Fluid Mech. 665, 357–381.Google Scholar
Pal, S., Deutsch, S. & Merkle, C. L. 1989 A comparison of shear stress fluctuation statistics between microbubble modified and polymer modified turbulent flow. Phys. Fluids A1, 1360–1362.CrossRefGoogle Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42, 89–109.CrossRefGoogle Scholar
Sanders, W. C., Winkel, E. S., Dowling, D. R., Perlin, M. & Ceccio, S. L. 2006 Bubble friction drag reduction in a high-Reynolds-number flat-plate turbulent boundary layer. J. Fluid Mech. 552, 353–380.Google Scholar
van den Berg, T. H., Luther, S., Lathrop, D. P. & Lohse, D. 2005 Drag reduction in bubbly Taylor–Couette turbulence. Phys. Rev. Lett. 94, 044501.Google Scholar
Watanabe, O., Masuko, A. & Shirose, Y. 1998 Measurements of drag reduction by microbubbles using very long ship models. J. Soc. Nav. Archit. Japan 183, 53–63.Google Scholar
White, C. M. & Mungal, M. G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 236–256.Google Scholar
Winkel, E. S., Oweis, G., Vanapalli, S. A., Dowling, D. R., Perlin, M., Solomon, M. J. & Ceccio, S. L. 2009 High Reynolds number turbulent boundary layer friction drag reduction from wall-injected polymer solutions. J. Fluid Mech. 621, 259–288.CrossRefGoogle Scholar
Wu, J. & Tulin, M. P. 1972 Drag reduction by ejecting additive solutions into pure-water boundary layer. Trans. ASME: J. Basic Engng 94, 749–756.CrossRefGoogle Scholar
Yao, C.-S., Lin, J. C. & Allan, B. G. 2002 Flow-field measurement of device-induced embedded streamwise vortex on a flate plate, 1st AIAA Flow Control Conference, St Louis, MO, Paper 2002-3162.Google Scholar