Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-13T01:28:42.008Z Has data issue: false hasContentIssue false
  • English
  • Français

On the sea spray aerosol originated from bubble bursting jets

Published online by Cambridge University Press:  10 January 2020

Francisco J. Blanco–Rodríguez Open the ORCID record for Francisco J. Blanco–Rodríguez [Opens in a new window]  and
J. M. Gordillo Open the ORCID record for J. M. Gordillo [Opens in a new window]
Francisco J. Blanco–Rodríguez
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
J. M. Gordillo*
Affiliation:
Área de Mecánica de Fluidos, Departamento de Ingeniería Aeroespacial y Mecánica de Fluidos, Universidad de Sevilla, Avenida de los Descubrimientos s/n 41092, Sevilla, Spain
*
†Email address for correspondence: jgordill@us.es
Get access Rights & Permissions [Opens in a new window]

Abstract

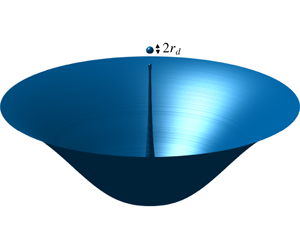
Here we provide a theoretical framework revealing that the radius $R_{d}$ of the top droplet ejected from a bursting bubble of radius $R_{b}$ and $Bo\leqslant 0.05$ can be expressed as $R_{d}/R_{b}=K_{b}(1-(Oh/Oh_{c}^{\prime })^{1/2})$ for $Oh\lesssim Oh_{c}^{\prime }$ or as $R_{d}\approx 18\,\unicode[STIX]{x1D707}_{l}^{2}/(\unicode[STIX]{x1D70C}_{l}\unicode[STIX]{x1D70E})$ for $Oh\gtrsim Oh_{c}^{\prime }$, with the numerically fitted constants $K_{b}\approx 0.2$, $Oh_{c}^{\prime }\approx 0.03$, $Oh=\unicode[STIX]{x1D707}_{l}/\sqrt{\unicode[STIX]{x1D70C}_{l}\,R_{b}\,\unicode[STIX]{x1D70E}}\ll 1$ the Ohnesorge number, $Bo=\unicode[STIX]{x1D70C}_{l}\,g\,R_{b}^{2}/\unicode[STIX]{x1D70E}$ the Bond number, and $\unicode[STIX]{x1D70C}_{l}$, $\unicode[STIX]{x1D707}_{l}$ and $\unicode[STIX]{x1D70E}$ indicating the liquid density, dynamic viscosity and interfacial tension coefficient, respectively. These predictions, which do not only have solid theoretical roots but are also much more accurate than the usual 10 % rule used in the context of marine spray generation via whitecaps for $R_{b}\lesssim 1$ mm, agree very well with both experimental data and numerical simulations for the values of $Oh$ and $Bo$ investigated. Moreover, making use of a criterion which reveals the mechanism that controls the growth rate of capillary instabilities, we also explain here why no droplets are ejected from the tip of the fast Worthington jet for $Oh\gtrsim 0.04$. In addition, our results predict the generation of submicron-sized aerosol particles with diameters below 100 nm and velocities ${\sim}\unicode[STIX]{x1D70E}/\unicode[STIX]{x1D707}_{l}$ for bubble radii $10~\unicode[STIX]{x03BC}\text{m}\lesssim R_{b}\lesssim 20~\unicode[STIX]{x03BC}\text{m}$, within the range found in natural conditions and in good agreement with experiments – a fact suggesting that our study could be applied in the modelling of sea spray aerosol production.

JFM classification

Drops and Bubbles: Aerosols/atomization Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Bubble dynamics
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 886 , 10 March 2020 , R2
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brasz, C. F., Bartlett, C. T., Walls, P. L. L., Flinn, E. G., Yu, Y. E. & Bird, J. C. 2018 Minimum size for the top jet drop from a bursting bubble. Phys. Rev. Fluids 3, 074001.CrossRefGoogle Scholar
Deike, L., Ghabache, E., G., L.-B., Das, A. K., Popinet, S. & Séon, T. 2018 Dynamics of jets produced by bursting bubbles. Phys. Rev. Fluids 3, 013603.CrossRefGoogle Scholar
Duchemin, L., Popinet, S., Josserand, C. & Zaleski, S. 2002 Jet formation in bubbles bursting at a free surface. Phys. Fluids 14 (9), 3000–3008.CrossRefGoogle Scholar
Erinin, M. A., Wang, S. D., Liu, R., Towle, D., Liu, X. & Duncan, J. H. 2019 Spray generation by a plunging breaker. Geophys. Res. Lett. 46 (14), 8244–8251.CrossRefGoogle Scholar
Gekle, S. & Gordillo, J. M. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 1. Jet formation. J. Fluid Mech. 663, 293–330.CrossRefGoogle Scholar
Ghabache, E., Antkowiak, A., Josserand, C. & Séon, T. 2014 On the physics of fizziness: how bubble bursting controls droplets ejection. Phys. Fluids 26, 121701.CrossRefGoogle Scholar
Gordillo, J. M. & Gekle, S. 2010 Generation and breakup of Worthington jets after cavity collapse. Part 2. Tip breakup of stretched jets. J. Fluid Mech. 663, 331–346.CrossRefGoogle Scholar
Gordillo, J. M. & Rodríguez-Rodríguez, J. 2019 Capillary waves control the ejection of bubble bursting jets. J. Fluid Mech. 867, 557–571.CrossRefGoogle Scholar
Lai, C.-Y., Eggers, J. & Deike, L. 2018 Bubble bursting: universal cavity and jet profiles. Phys. Rev. Lett. 121, 144501.CrossRefGoogle ScholarPubMed
de Leeuw, G., Andreas, E. L., Anguelova, M. D., Fairall, C. W., Lewis, E. R., O’Dowd, C., Schulz, M. & Schwartz, S. E. 2011 Production flux of sea spray aerosol. Rev. Geophys. 49, 2010RG000349.CrossRefGoogle Scholar
Lhuissier, H. & Villermaux, E. 2012 Bursting bubble aerosols. J. Fluid Mech. 696, 5–44.CrossRefGoogle Scholar
MacIntyre, F. 1972 Flow patterns in breaking bubbles. J. Geophys. Res. 77, 5211–5225.CrossRefGoogle Scholar
Nayar, K. G., Sharqawy, M. H., Banchik, L. D. & Lienhard V, J. H. 2016 Thermophysical properties of seawater: a review and new correlations that include pressure dependence. Desalination 390, 1–24.CrossRefGoogle Scholar
Popinet, S. 2003 Gerris: a tree-based adaptive solver for the incompressible Euler equations in complex geometries. J. Comput. Phys. 190 (2), 572–600.CrossRefGoogle Scholar
Rayleigh, L. 1878 On the instability of jets. Proc. Lond. Math. Soc. s1–10 (1), 4–13.CrossRefGoogle Scholar
Taylor, G. I. 1959 The dynamics of thin sheets of fluid. III. Desintegration of fluid sheets. Proc. R. Soc. Lond. A 253, 1274.Google Scholar
Veron, F. 2015 Ocean spray. Annu. Rev. Fluid Mech. 47, 507–538.CrossRefGoogle Scholar
Wang, X., Deane, G. B., Moore, K. A., Ryder, O. S., Stokes, M. D., Beall, C. M., Collins, D. B., Santander, M. V., Burrows, S. M., Sultana, C. M. et al. 2017 The role of jet and film drops in controlling the mixing state of submicron sea spray aerosol particles. Proc. Natl Acad. Sci. USA 114 (27), 6978–6983.CrossRefGoogle ScholarPubMed
Zeff, B. W., Kleber, B., Fineberg, J. & Lathrop, D. P. 2000 Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 403, 401–404.CrossRefGoogle ScholarPubMed
Supplementary material: File

Blanco–Rodríguez and Gordillo supplementary material

Blanco–Rodríguez and Gordillo supplementary material

Download Blanco–Rodríguez and Gordillo supplementary material(File)
File 438.7 KB