Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Batlle Martin, Marc
Harris, Jeffrey C.
Filipot, Jean-François
Hulin, Florian
Tassin, Alan
and
Renaud, Paul
2023.
Deep water focused breaking wave loads on a fixed cylinder.
Coastal Engineering,
Vol. 186,
Issue. ,
p.
104397.
Hu, Zhengyu
and
Li, Yuzhu
2023.
Two-dimensional simulations of large-scale violent breaking wave impacts on a flexible wall.
Coastal Engineering,
Vol. 185,
Issue. ,
p.
104370.
Li, Jiale
Lian, Jijian
Wang, Haijun
Guo, Yaohua
Liu, Sha
Zhang, Yutong
and
Zhang, FengWu
2023.
Numerical study of the local scour characteristics of bottom-supported installation platforms during the installation of a monopile.
Ships and Offshore Structures,
p.
1.
Brown, S.A.
Tosdevin, T.
Jin, S.
Hann, M.
Simmonds, D.
and
Greaves, D.M.
2023.
On the selection of design waves for predicting extreme motions of a floating offshore wind turbine.
Ocean Engineering,
Vol. 290,
Issue. ,
p.
116400.
Gong, Yigang
and
Wang, Jiasong
2024.
Turbulence model adaptability at critical Reynolds numbers and applications in wake control via fairings.
Applied Ocean Research,
Vol. 153,
Issue. ,
p.
104263.
Landesman, Paul
Harris, Jeffrey C.
Peyrard, Christophe
and
Benoit, Michel
2024.
Wave–structure interaction by a two–way coupling between a fully nonlinear potential flow model and a Navier–Stokes solver.
Ocean Engineering,
Vol. 308,
Issue. ,
p.
118209.
Khan, Muhammad Ahsan
Barajas, Gabriel
Gaeta, Maria Gabriella
Lara, Javier Lopez
and
Archetti, Renata
2024.
Hydrodynamic analysis and optimization of a floating wave energy converter with moonpool using OpenFOAM®.
Applied Ocean Research,
Vol. 142,
Issue. ,
p.
103847.
Altomare, Corrado
Li, Yuzhu Pearl
and
Tafuni, Angelantonio
2025.
Exploring Dissipation Terms in the SPH Momentum Equation for Wave Breaking on a Vertical Pile.
Journal of Marine Science and Engineering,
Vol. 13,
Issue. 6,
p.
1005.
Wang, Limeng
Zou, Zhili
Yan, Kai
and
Chen, Qiupan
2025.
Experimental investigation into the diffraction of propagating L1-type crescent waves by a circular cylinder.
Ocean Engineering,
Vol. 332,
Issue. ,
p.
121219.
Li, Biao
Qi, Wen-Gang
Gao, Fu-Ping
He, Ben
and
Yang, Li-Jing
2025.
Experimental investigation of scour effects on regular and breaking wave loads on a monopile.
Coastal Engineering,
Vol. 197,
Issue. ,
p.
104696.
Hu, Zhengyu
and
Li, Yuzhu Pearl
2025.
Breaking wave impacts on an elastic plate.
Journal of Fluid Mechanics,
Vol. 1015,
Issue. ,
Harris, Jeffrey C.
2025.
Faster than real-time, phase-resolving, data-driven model of wave propagation and wave–structure interaction.
Applied Ocean Research,
Vol. 154,
Issue. ,
p.
104291.
Tan, Weikai
Ren, Pu
Cao, Deping
Liang, Hui
and
Chen, Hao
2025.
Data-driven modelling of fully nonlinear wave loads on offshore wind-turbine monopiles at prototype scale.
Marine Structures,
Vol. 101,
Issue. ,
p.
103775.
Zhao, Xuanlie
Pan, Shiqi
Zou, Qingping
and
Geng, Jing
2025.
Slamming loads induced by dam-break flow on land-based oscillating water columns: Numerical and experimental study.
Coastal Engineering,
Vol. 198,
Issue. ,
p.
104715.
Chew, L. W.
Melaku, A. F.
Ciarlatani, M. F.
and
Gorlé, C.
2025.
Sensitivity of inflow turbulence uncertainty on wind pressure on high‐rise buildings using large eddy simulations.
Computer-Aided Civil and Infrastructure Engineering,
Vol. 40,
Issue. 22,
p.
3430.
Chen, Weilin
and
Li, Yuzhu Pearl
2025.
Simulation of a wall-mounted stem in uniform flow.
Journal of Fluid Mechanics,
Vol. 1013,
Issue. ,
Liong, Ching Theng
Yang, Xiaoxiao
Chan, Eng Soon
and
Low, Ying Min
2025.
Mechanics of energy dissipation due to wave plunging.
Coastal Engineering,
Vol. 198,
Issue. ,
p.
104723.
Myklebust, Fredrik Dubay
Fuhrman, David R.
and
Li, Yuzhu Pearl
2025.
Tensor basis neural networks for unsteady turbulent flow prediction.
Physics of Fluids,
Vol. 37,
Issue. 7,
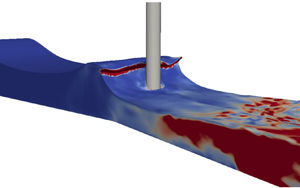
 $\omega$ turbulence model. Comparison of results simulated with a stabilized two-equation turbulence model, as well as no turbulence model, demonstrates that the breaking point and the peak force on a vertical cylinder due to incipient breaking should not be affected by the turbulence closure model, provided that it is stable and the simulations are converged. Notably, the present results show that the build-up to peak force induced by incipient wave breaking can be accurately predicted without any turbulence closure model. However, for the prediction of the secondary load cycle (SLC), proper turbulence modelling is required, as this process involves both turbulence production and lee-side flow separation. The Reynolds stress–
$\omega$ turbulence model. Comparison of results simulated with a stabilized two-equation turbulence model, as well as no turbulence model, demonstrates that the breaking point and the peak force on a vertical cylinder due to incipient breaking should not be affected by the turbulence closure model, provided that it is stable and the simulations are converged. Notably, the present results show that the build-up to peak force induced by incipient wave breaking can be accurately predicted without any turbulence closure model. However, for the prediction of the secondary load cycle (SLC), proper turbulence modelling is required, as this process involves both turbulence production and lee-side flow separation. The Reynolds stress– $\omega$ model is demonstrated to predict the SLC more accurately than a stabilized two-equation
$\omega$ model is demonstrated to predict the SLC more accurately than a stabilized two-equation  $k$–
$k$– $\omega$ turbulence model, as the flow separation points and vorticity field are better predicted. Some existing studies indicate that the generation of the SLC does not necessarily result from flow separation, but is rather due to the suction force. The present work finds that the occurrence and point of flow separation significantly affect the magnitude of the suction force, which hence affects the SLC prediction significantly. For waves breaking on a vertical pile, proper turbulence modelling is therefore essential for accurate SLC predictions. (In the above,
$\omega$ turbulence model, as the flow separation points and vorticity field are better predicted. Some existing studies indicate that the generation of the SLC does not necessarily result from flow separation, but is rather due to the suction force. The present work finds that the occurrence and point of flow separation significantly affect the magnitude of the suction force, which hence affects the SLC prediction significantly. For waves breaking on a vertical pile, proper turbulence modelling is therefore essential for accurate SLC predictions. (In the above,  $k$ is the turbulent kinetic energy density and
$k$ is the turbulent kinetic energy density and  $\omega$ is the specific dissipation rate.)
$\omega$ is the specific dissipation rate.)

