Article contents
Onset of Darcy–Bénard convection in a horizontal layer of dual-permeability medium with isothermal boundaries
Published online by Cambridge University Press: 21 July 2020
Abstract
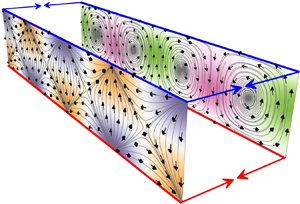
The onset of natural convection in an infinite horizontal layer of a fractured-porous medium is investigated. The breakdown of local equilibrium between the low-permeability matrix and fractures embedded in the matrix is accounted for by applying the dual-porosity dual-permeability model. The symmetric case of impermeable and isothermal boundaries of the layer is examined in detail. By means of linear perturbation analysis, the dispersion equation is derived, and its solutions are investigated numerically as well as analytically in a few asymptotic cases. It is determined that the critical Rayleigh number depends only on the permeability, heat conductivity ratios and the coefficient of heat and mass transfer between fractures and matrix. It is shown that the convection exhibits a rich variety of flow patterns at near-critical conditions. Nine flow regimes can arise with co-rotating or counter-rotating convection cells in the fractures and matrix. These modes can bifurcate to the plane flow regime, in which only cross-medium convection occurs. The complete classification of the flow regimes is provided and plotted in a solution map. Finally, the theoretical analysis is supported by the numerical modelling of the convection by using a reservoir simulator.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by

