Article contents
Opposing-buoyancy mixed convection through and around arrays of heated cylinders
Published online by Cambridge University Press: 23 September 2022
Abstract
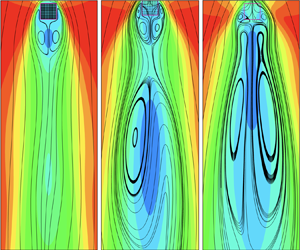
We numerically investigated the opposing-buoyancy mixed convection through and around square arrays of  $10\times 10$ heated circular cylinders with the solid fraction (
$10\times 10$ heated circular cylinders with the solid fraction ( $\phi$) ranging from 0.0079 to 0.66 and the Richardson number (
$\phi$) ranging from 0.0079 to 0.66 and the Richardson number ( $Ri$) varying from 0 to 1 at a fixed Reynolds number (
$Ri$) varying from 0 to 1 at a fixed Reynolds number ( $Re$) of 100. Our simulations revealed that the large mean recirculation in the far wake can be detached from or connected with the vortex pair in the near wake for different combinations of
$Re$) of 100. Our simulations revealed that the large mean recirculation in the far wake can be detached from or connected with the vortex pair in the near wake for different combinations of  $Ri$ and
$Ri$ and  $\phi$. Also, it was found that the array with relatively small
$\phi$. Also, it was found that the array with relatively small  $\phi$ can significantly promote flow instability even at moderate
$\phi$ can significantly promote flow instability even at moderate  $Ri$. The instability, which is closely related to the fluctuating heat flux, develops from the lateral sides to the downstream side of the array and gives rise to the large mean recirculation in the far wake. The power spectra density of the array-scale force coefficients demonstrates that the flow undergoes different bifurcation behaviours under various parameter combinations, which reflects the interaction between the near-wake and far-wake vortexes. Interestingly, the Strouhal–Richardson number curves can be collapsed onto the same curve when
$Ri$. The instability, which is closely related to the fluctuating heat flux, develops from the lateral sides to the downstream side of the array and gives rise to the large mean recirculation in the far wake. The power spectra density of the array-scale force coefficients demonstrates that the flow undergoes different bifurcation behaviours under various parameter combinations, which reflects the interaction between the near-wake and far-wake vortexes. Interestingly, the Strouhal–Richardson number curves can be collapsed onto the same curve when  $Ri$ is increased by a
$Ri$ is increased by a  $\phi$-dependent factor. Also, for
$\phi$-dependent factor. Also, for  $\phi \leqslant 0.22$, both the mean drag coefficient and the mean Nusselt number of the array were found to decrease linearly with
$\phi \leqslant 0.22$, both the mean drag coefficient and the mean Nusselt number of the array were found to decrease linearly with  $Ri$ since the buoyancy within the array becomes prominent in this range of
$Ri$ since the buoyancy within the array becomes prominent in this range of  $\phi$.
$\phi$.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by


