Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T07:15:57.912Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal dynamo action by steady flows confined to a cube

Published online by Cambridge University Press:  13 October 2015

L. Chen ,
W. Herreman  and
A. Jackson
L. Chen
Affiliation:
Institute of Geophysics, ETH Zurich, Sonneggstrasse 5, 8092 Zurich, Switzerland
W. Herreman*
Affiliation:
LIMSI-CNRS, Université Paris Sud 11, 91403 Orsay, France
A. Jackson
Affiliation:
Institute of Geophysics, ETH Zurich, Sonneggstrasse 5, 8092 Zurich, Switzerland
*
†Email address for correspondence: wietze@limsi.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Many flows of electrically conducting fluids can spontaneously generate magnetic fields through the process of dynamo action, but when does a flow produce a better dynamo than another one or when is it simply the most efficient dynamo? Using a variational approach close to that of Willis (Phys. Rev. Lett., vol. 109, 2012, 251101), we find optimal kinematic dynamos within a huge class of stationary and incompressible flows that are confined in a cube. We demand that the magnetic field satisfies either superconducting (T) or pseudovacuum (N) boundary conditions on opposite pairs of walls of the cube, which results in four different combinations. For each of these set-ups, we find the optimal flow and its corresponding magnetic eigenmodes. Numerically, it is observed that swapping the magnetic boundary from T to N leaves the magnetic energy growth nearly unchanged, and both 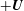$+\boldsymbol{U}$ and 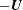$-\boldsymbol{U}$ are optimal flows for these different but complementary set-ups. This can be related to work by Favier & Proctor (Phys. Rev. E, vol. 88, 2013, 031001). We provide minimal lower bounds for dynamo action and find that no dynamo is possible below an enstrophy (or shear) based magnetic Reynolds number 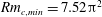$Rm_{c,min}=7.52{\rm\pi}^{2}$, which is a factor of 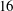$16$ above the Proctor/Backus bound.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory Geophysical and Geological Flows: Geophysical and Geological Flows Mathematical Foundations: Variational methods
Type
Papers
Information
Journal of Fluid Mechanics , Volume 783 , 25 November 2015 , pp. 23 - 45
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alexakis, A. 2011 Searching for the fastest dynamo: laminar ABC flows. Phys. Rev. E 84 (2), 026321.Google Scholar
Arnold, V. I. & Korkina, E. I. 1983 The growth of a magnetic field in a three dimensional steady incompressible flow. Vestnik Moskov. Univ. Ser. I Mat. Mekh. 3, 43–46.Google Scholar
Backus, G. 1958 A class of self-sustaining dissipative spherical dynamos. Ann. Phys. 4 (4), 372–447.Google Scholar
Bouya, I. & Dormy, E. 2013 Revisiting the ABC flow dynamo. Phys. Fluids 25, 037103.Google Scholar
Duguet, Y., Monokrousos, A., Brandt, L. & Henningson, D. S. 2013 Minimal transition thresholds in plane Couette flow. Phys. Fluids 25 (8), 084103.Google Scholar
Favier, B. & Proctor, M. R. E. 2013 Growth rate degeneracies in kinematic dynamos. Phys. Rev. E 88 (3), 031001.Google Scholar
Galloway, D. & Frisch, U. 1984 A numerical investigation of magnetic field generation in a flow with chaotic streamlines. Geophys. Astrophys. Fluid Dyn. 29 (1–4), 13–18.CrossRefGoogle Scholar
Holme, R. 2003 Optimised axially-symmetric kinematic dynamos. Phys. Earth Planet. Inter. 140 (1), 3–11.CrossRefGoogle Scholar
Kerswell, R. R., Pringle, C. C. T. & Willis, A. P. 2014 An optimization approach for analysing nonlinear stability with transition to turbulence in fluids as an exemplar. Rep. Prog. Phys. 77 (8), 085901.CrossRefGoogle ScholarPubMed
Khalzov, I. V., Brown, B. P., Cooper, C. M., Weisberg, D. B. & Forest, C. B. 2012 Optimized boundary driven flows for dynamos in a sphere. Phys. Plasmas 19 (11), 112106.Google Scholar
Krstulovic, G., Thorner, G., Vest, J.-P., Fauve, S. & Brachet, M. 2011 Axial dipolar dynamo action in the Taylor–Green vortex. Phys. Rev. E 84 (6), 066318.CrossRefGoogle ScholarPubMed
Li, K., Jackson, A. & Livermore, P. W. 2011 Variational data assimilation for the initial-value dynamo problem. Phys. Rev. E 84 (5), 056321.CrossRefGoogle ScholarPubMed
Li, K., Jackson, A. & Livermore, P. W. 2014 Variational data assimilation for a forced, inertia-free magnetohydrodynamic dynamo model. Geophys. J. Intl 199 (3), 1662–1676.Google Scholar
Lions, J. L. 1970 Optimal Control of Systems Governed by Partial Differential Equations. Springer.Google Scholar
Love, J. J. & Gubbins, D. 1996 Optimized kinematic dynamos. Geophys. J. Intl 124 (3), 787–800.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105 (15), 154502.Google Scholar
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 702, 415–443.CrossRefGoogle Scholar
Proctor, M. R. E. 1977 On Backus’ necessary condition for dynamo action in a conducting sphere. Geophys. Astrophys. Fluid Dyn. 9, 89–93.CrossRefGoogle Scholar
Roberts, G. O. 1972 Dynamo action of fluid motions with two-dimensional periodicity. Phil. Trans. R. Soc. Lond. A 271 (1216), 411–454.Google Scholar
Stefani, F., Gerbeth, G. & Gailitis, A. 1999 Velocity profile optimization for the Riga dynamo experiment. In Transfer Phenomena in Magnetohydrodynamic and Electroconducting Flows, pp. 31–44. Springer.Google Scholar
Talagrand, O. & Courtier, P. 1987 Variational assimilation of meteorological observations with the adjoint vorticity equation. I: theory. Q. J. R. Meteorol. Soc. 113 (478), 1311–1328.CrossRefGoogle Scholar
Tarantola, A. 1984 Inversion of seismic reflection data in the acoustic approximation. Geophysics 49 (8), 1259–1266.CrossRefGoogle Scholar
Tromp, J., Komattisch, D. & Liu, Q. 2008 Spectral-element and adjoint methods in seismology. Commun. Comput. Phys. 3 (1), 1–32.Google Scholar
Willis, A. P. 2012 Optimization of the magnetic dynamo. Phys. Rev. Lett. 109 (25), 251101.Google Scholar