Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T01:44:40.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimal growth over a time-evolving variable-density jet at Atwood number 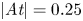$\vert \textit {At} \vert = 0.25$

Published online by Cambridge University Press:  11 February 2022

Gabriele Nastro Open the ORCID record for Gabriele Nastro [Opens in a new window] ,
Jérôme Fontane Open the ORCID record for Jérôme Fontane [Opens in a new window]  and
Laurent Joly Open the ORCID record for Laurent Joly [Opens in a new window]
Gabriele Nastro*
Affiliation:
ISAE-SUPAERO, Université de Toulouse, France
Jérôme Fontane
Affiliation:
ISAE-SUPAERO, Université de Toulouse, France
Laurent Joly
Affiliation:
ISAE-SUPAERO, Université de Toulouse, France
*
†Email address for correspondence: nastrogabriele@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Secondary instabilities growing over a time-evolving variable-density round jet subject to the primary Kelvin–Helmholtz (KH) instability at Atwood number $\vert \textit {At} \vert = 0.25$ are investigated with a non-modal linear stability analysis. Despite local modifications of the base flow vorticity induced by the baroclinic torque, these disturbances experience a short-term universal growth due to a combination of the Orr and lift-up mechanisms, whatever the azimuthal wavenumber $m$. At $\textit {Re}=1000$, the secondary energy growth stems from the development of elliptical and hyperbolic instabilities, with an E-type-to-H-type transition as $m$ and $\textit {Re}$ increase, as in the homogeneous case (Nastro et al., J. Fluid Mech., vol. 900, 2020, A13). In the light jet at $\textit {Re} = 1000$, after the KH mode saturation, the high-$m$ H-type instability is replaced by a perturbation organised as counter-rotating streamwise vortices located in the base flow region of promoted strain rate. Increasing the Reynolds number up to $\textit {Re} = 10\,000$ yields larger energy growths and a strong anisotropy among energy and enstrophy components with a preferential increase of axial velocity and azimuthal vorticity. Both come from the linearised baroclinic source that drives the optimal response towards folded sheets of axial velocity that differ from those observed in the variable-density plane shear layers. When the perturbation is injected around the KH saturation time for $\textit {Re}=10\,000$, the response to optimal perturbation takes the form of fast growing secondary KH instabilities whatever $m$. We find these three-dimensional secondary KH instabilities to be good candidates for the transition to turbulence in variable-density jet flows.

JFM classification

Wakes/Jets: Jets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 936 , 10 April 2022 , A15
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arratia, C., Caulfield, C.P. & Chomaz, J.-M. 2013 Transient perturbation growth in time-dependent mixing layers. J. Fluid Mech. 717, 90–133.CrossRefGoogle Scholar
Batchelor, G.K. & Gill, A.E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14 (4), 529–551.CrossRefGoogle Scholar
Becker, H.A. & Massaro, T.A. 1968 Vortex evolution in a round jet. J. Fluid Mech. 31 (3), 435–448.CrossRefGoogle Scholar
Brancher, P., Chomaz, J.-M. & Huerre, P. 1994 Direct numerical simulations of round jets: vortex induction and side jets. Phys. Fluids 6 (5), 1768–1774.CrossRefGoogle Scholar
Coenen, W., Lesshafft, L., Garnaud, X. & Sevilla, A. 2017 Global instability of low-density jets. J. Fluid Mech. 820, 187–207.CrossRefGoogle Scholar
Corbett, P. & Bottaro, A. 2000 Optimal perturbations for boundary layers subject to stream-wise pressure gradient. Phys. Fluids 12 (1), 120–130.CrossRefGoogle Scholar
Corbett, P. & Bottaro, A. 2001 Optimal linear growth in swept boundary layers. J. Fluid Mech. 435, 1–23.CrossRefGoogle Scholar
Crighton, D.G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77 (2), 397–413.CrossRefGoogle Scholar
Dimotakis, P.E. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24 (11), 1791–1796.CrossRefGoogle Scholar
Drazin, P.G. & Reid, W.H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18 (4), 487–488.CrossRefGoogle Scholar
Farrell, B.F. 1988 Optimal excitation of perturbations in viscous shear flow. Phys. Fluids 31 (8), 2093–2102.CrossRefGoogle Scholar
Farrell, B.F. & Ioannou, P.J. 1993 Perturbation growth in shear flow exhibits universality. Phys. Fluids A 5 (9), 2298–2300.CrossRefGoogle Scholar
Fontane, J. 2005 Transition des écoulements cisaillés libres à densité variable. PhD thesis, Institut National Polytechnique de Toulouse, France.Google Scholar
Fontane, J. & Joly, L. 2008 The stability of the variable-density Kelvin–Helmholtz billow. J. Fluid Mech. 612, 237–260.CrossRefGoogle Scholar
Fontane, J., Joly, L. & Reinaud, J.N. 2008 Fractal Kelvin–Helmholtz breakups. Phys. Fluids 20 (9), 091109.CrossRefGoogle Scholar
Foures, D.P.G., Caulfield, C.P. & Schmid, P.J. 2014 Optimal mixing in two-dimensional plane Poiseuille flow at finite Péclet number. J. Fluid Mech. 748, 241–277.CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P.J. & Huerre, P. 2013 a Modal and transient dynamics of jet flows. Phys. Fluids 25 (4), 044103.CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P.J. & Huerre, P. 2013 b The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.CrossRefGoogle Scholar
Gunzburger, M. 2002 Perspectives in Flow Control and Optimization. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Hallberg, M.P. & Strykowski, P.J. 2006 On the universality of global modes in low-density axisymmetric jets. J. Fluid Mech. 569, 493–507.CrossRefGoogle Scholar
Jendoubi, S. & Strykowski, P.J. 1994 Absolute and convective instability of axisymmetric jets with external flow. Phys. Fluids 6 (9), 3000–3009.CrossRefGoogle Scholar
Jimenez-Gonzalez, J.I. & Brancher, P. 2017 Transient energy growth of optimal streaks in parallel round jets. Phys. Fluids 29 (11), 114101.CrossRefGoogle Scholar
Jimenez-Gonzalez, J.I., Brancher, P. & Martinez-Bazan, C. 2015 Modal and non-modal evolution of perturbations for parallel round jets. Phys. Fluids 27 (4), 044105.CrossRefGoogle Scholar
Joly, L., Fontane, J. & Chassaing, P. 2005 The Rayleigh–Taylor instability of two-dimensional high-density vortices. J. Fluid Mech. 537, 415–431.CrossRefGoogle Scholar
Joly, L. & Reinaud, J.N. 2007 The merger of two-dimensional radially stratified high-Froude-number vortices. J. Fluid Mech. 582, 133–151.CrossRefGoogle Scholar
Joseph, D.D. 1990 Fluid dynamics of two miscible liquids with diffusion and gradient stresses. Eur. J. Mech. (B/Fluids) 9 (6), 565–596.Google Scholar
Klaassen, G.P. & Peltier, W.R. 1991 The influence of stratification on secondary instability in free shear layers. J. Fluid Mech. 227, 71–106.CrossRefGoogle Scholar
Kyle, D.M. & Sreenivasan, K.R 1993 The instability and breakdown of a round variable density jet. J. Fluid Mech. 249, 619–664.CrossRefGoogle Scholar
Landhal, M.T. 1975 Wave breakdown and turbulence. SIAM J. Appl. Maths 28 (4), 735–756.CrossRefGoogle Scholar
Landhal, M.T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98 (2), 243–251.CrossRefGoogle Scholar
Lessen, M.P. & Singh, P.J. 1973 The stability of axisymmetric free shear layers. J. Fluid Mech. 60 (3), 433–457.CrossRefGoogle Scholar
Lesshafft, L. & Huerre, P. 2007 Linear impulse response in hot round jets. Phys. Fluids 19 (2), 024102.CrossRefGoogle Scholar
Lesshafft, L., Huerre, P. & Sagaut, P. 2007 Frequency selection in globally unstable round jets. Phys. Fluids 19 (5), 054108.CrossRefGoogle Scholar
Lesshafft, L., Huerre, P., Sagaut, P. & Terracol, M. 2006 Nonlinear global modes in hot jets. J. Fluid Mech. 554, 393–409.CrossRefGoogle Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.CrossRefGoogle Scholar
Lopez-Zazueta, A., Fontane, J. & Joly, L. 2016 Optimal perturbations in time-dependent variable-density Kelvin–Helmholtz billows. J. Fluid Mech. 803, 466–501.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 1998 Görtler vortices: a backward-in-time approach to the receptivity problem. J. Fluid Mech. 363, 1–23.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2001 Linear stability and receptivity analyses of the stokes layer produced by an impulsively started plate. Phys. Fluids 13 (6), 1668–1678.CrossRefGoogle Scholar
Michalke, A. 1971 Instabilität eines kompressiblen runden freistrahls unter berücksichtigung des einflusses des strahlgrenzschichtdicke. Z. Flugwiss. 8–9, 319–328.Google Scholar
Michalke, A. 1984 Survey on jet instability theory. Prog. Aerosp. Sci. 21, 159–199.CrossRefGoogle Scholar
Monkewitz, P.A. & Bechert, D.W. 1988 Self-excited oscillations and mixing in a hot jet. Phys. Fluids 31 (9), 2386–2386.CrossRefGoogle Scholar
Monkewitz, P.A., Bechert, D.W., Barsikow, B. & Lehmann, B. 1990 Self-excited oscillations and mixing in a heated round jet. J. Fluid Mech. 213, 611–639.CrossRefGoogle Scholar
Monkewitz, P.A., Lehmann, B., Barsikow, B. & Bechert, D.W. 1989 The spreading of self-excited hot jets by side jets. Phys. Fluids 1 (3), 446–448.CrossRefGoogle Scholar
Monkewitz, P.A. & Pfizenmaier, E. 1991 Mixing by side jets in strongly forced and self-excited round jets. Phys. Fluids 3 (5), 1356–1361.CrossRefGoogle Scholar
Morris, P.J. 1976 The spatial viscous instability of axisymmetric jets. J. Fluid Mech. 77 (3), 511–529.CrossRefGoogle Scholar
Moser, R.D. & Rogers, M.M. 1993 The three-dimensional evolution of a plane mixing layer: pairing and transition to turbulence. J. Fluid Mech. 247, 275–320.CrossRefGoogle Scholar
Nastro, G. 2020 Stabilité non-modale des jets ronds inhomogènes. PhD thesis, Université de Toulouse, Institut Supérieur de l'Aéronautique et de l'Espace.Google Scholar
Nastro, G., Fontane, J. & Joly, L. 2020 Optimal perturbations in viscous round jets subject to Kelvin–Helmholtz instability. J. Fluid Mech. 900, A13.CrossRefGoogle Scholar
Nichols, J.W., Schmid, P.J. & Riley, J.J. 2007 Self-sustained oscillations in variable-density round jets. J. Fluid Mech. 582, 341–376.CrossRefGoogle Scholar
Orr, W.M.F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I: A perfect liquid. Part II: A viscous liquid. Proc. R. Irish Acad. A: Math. Phys. Sci. 27, 9–138.Google Scholar
Ortiz, S. & Chomaz, J.-M. 2011 Transient growth of secondary instabilities in parallel wakes: anti lift-up mechanism and hyperbolic instability. Phys. Fluids 23 (11), 114106.CrossRefGoogle Scholar
Plaschko, P. 1979 Helical instabilities of slowly divergent jets. J. Fluid Mech. 92, 209–215.CrossRefGoogle Scholar
Rayleigh, J.W.S. 1892 Scientific Papers, vol. 3, Cambridge Library Collection – Mathematics. Cambridge University Press.Google Scholar
Reinaud, J.M., Joly, L. & Chassaing, P. 2000 The baroclinic secondary instability of the two-dimensional shear layer. Phys. Fluids 12 (10), 2489–2505.CrossRefGoogle Scholar
Rogers, M.M & Moser, R.D. 1993 Spanwise scale selection in plane mixing layers. J. Fluid Mech. 247, 321–337.CrossRefGoogle Scholar
Sandoval, D.L. 1995 The dynamics of variable-density turbulence. PhD thesis, University of Washington, USA.CrossRefGoogle Scholar
Schmid, P.J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39 (1), 129–162.CrossRefGoogle Scholar