Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T23:48:11.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Optimising the flow through a concertinaed filtration membrane

Published online by Cambridge University Press:  26 February 2021

Victoria E. Pereira Open the ORCID record for Victoria E. Pereira [Opens in a new window] ,
Mohit P. Dalwadi Open the ORCID record for Mohit P. Dalwadi [Opens in a new window] ,
Enrique Ruiz-Trejo Open the ORCID record for Enrique Ruiz-Trejo [Opens in a new window]  and
Ian M. Griffiths Open the ORCID record for Ian M. Griffiths [Opens in a new window]
Victoria E. Pereira
Affiliation:
Mathematical Institute, University of Oxford, OxfordOX2 6GG, UK
Mohit P. Dalwadi
Affiliation:
Mathematical Institute, University of Oxford, OxfordOX2 6GG, UK
Enrique Ruiz-Trejo
Affiliation:
Smart Separations Ltd., 40 Occam Rd, GuildfordGU2 7YG, UK
Ian M. Griffiths*
Affiliation:
Mathematical Institute, University of Oxford, OxfordOX2 6GG, UK
*
†Email address for correspondence: ian.griffiths@maths.ox.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

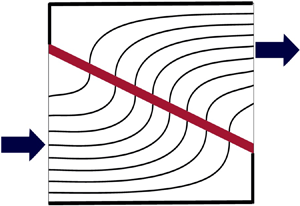
Membrane filtration is a vital industrial process, with applications including air purification and blood filtration. In this paper, we study the optimal design for a concertinaed filtration membrane composed of angled porous membranes and dead ends. The geometry of the filter motivates a lubrication scaling for the flow, leading to a system of coupled (modified) Reynolds equations. By analysing this reduced system, we examine how the filter performance depends on the angle, position, thickness and permeance of the membrane, using a combination of numerical and asymptotic approaches, the latter in the limit of a slightly angled membrane. We find that, for a membrane of fixed angle and physical properties, there can exist multiple membrane positions that maximise the flux for an applied pressure difference. More generally, this shows how coupled problems in lubrication flow can exhibit non-trivial bifurcating optima. For the particular application on which we focus, we show that, while the maximal flux achievable depends on the membrane thickness and permeance, the optimal membrane configuration is always in one of two set-ups: centred and diagonal across the full domain; or angled and in the corner of the domain.

JFM classification

Low-Reynolds-number flows: Porous media Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A28
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Beavers, G.S. & Joseph, D.D. 1967 Boundary conditions at a naturally permeable wall. J. Fluid Mech. 30 (1), 197–207.CrossRefGoogle Scholar
Caesar, T. & Schroth, T. 2002 The influence of pleat geometry on the pressure drop in deep-pleated cassette filters. Filtr. Separat. 39 (9), 48–54.CrossRefGoogle Scholar
Chen, D.R., Pui, D.Y.H. & Liu, B.Y.H. 1995 Optimization of pleated filter designs using a finite-element numerical model. Aerosol Sci. Technol. 23 (4), 579–590.CrossRefGoogle Scholar
Griffiths, I.M., Howell, P.D. & Shipley, R.J. 2013 Control and optimization of solute transport in a thin porous tube. Phys. Fluids 25 (3), 033101.CrossRefGoogle Scholar
Herterich, J.G., Xu, Q., Field, R.W., Vella, D. & Griffiths, I.M. 2017 Optimizing the operation of a direct-flow filtration device. J. Engng Maths 104 (1), 195–211.CrossRefGoogle Scholar
King, J.R. & Please, C.P. 1996 Asymptotic analysis of the growth of cake layers in filters. IMA J. Appl. Maths 57 (1), 1–28.CrossRefGoogle Scholar
Lee, K.P., Arnot, T.C. & Mattia, D. 2011 A review of reverse osmosis membrane materials for desalination—Development to date and future potential. J. Membr. Sci. 370 (1–2), 1–22.CrossRefGoogle Scholar
Noble, R.D. & Stern, S.A. 1995 Membrane Separations Technology: Principles and Applications. Elsevier.Google Scholar
Rebaï, M., Prat, M., Meireles, M., Schmitz, P. & Baclet, R. 2010 A semi-analytical model for gas flow in pleated filters. Chem. Engng Sci. 65 (9), 2835–2846.CrossRefGoogle Scholar
van Reis, R. & Zydney, A. 2007 Bioprocess membrane technology. J. Membr. Sci. 297 (1–2), 16–50.CrossRefGoogle Scholar
Saleh, A.M., Tafreshi, H.V. & Pourdeyhimi, B. 2016 An analytical approach to predict pressure drop and collection efficiency of dust-load pleated filters. Sep. Purif. Technol. 161, 80–87.CrossRefGoogle Scholar
Sanaei, P., Richardson, G.W., Witelski, T. & Cummings, L.J. 2016 Flow and fouling in a pleated membrane filter. J. Fluid Mech. 795, 36–59.CrossRefGoogle Scholar
Smart Separations Ltd 2020 https://smartseparations.com/.Google Scholar
Sun, Y., Sanaei, P., Kondic, L. & Cummings, L.J. 2020 Modeling and design optimization for pleated membrane filters. Phys. Rev. Fluids 5 (4), 044306.CrossRefGoogle Scholar
Théron, F., Joubert, A. & Le Coq, L. 2017 Numerical and experimental investigations of the influence of the pleat geometry on the pressure drop and velocity field of a pleated fibrous filter. Sep. Purif. Technol. 182, 69–77.CrossRefGoogle Scholar
Wang, M., Mondal, S. & Griffiths, I.M. 2017 The role of fouling in optimizing direct-flow filtration module design. Chem. Engng Sci. 163, 215–222.CrossRefGoogle Scholar
Xu, Q., Pearce, G.K. & Field, R.W. 2017 Pressure driven inside feed (PDI) hollow fibre filtration: optimizing the geometry and operating parameters. J. Membr. Sci. 537, 323–336.CrossRefGoogle Scholar