1. Introduction
Particles in a fluid subjected to a bulk deformation interact with each other hydrodynamically, modifying the rheology of suspensions, and can lead to flow-induced microstructuring (Stickel & Powell Reference Stickel and Powell2005; Van der Sman Reference Van der Sman2009; Denn & Morris Reference Denn and Morris2014; Tanner Reference Tanner2018; Carotenuto et al. Reference Carotenuto, Rexha, Martone and Minale2021). Flow-induced microstructure in flowing suspensions is a key to understanding a diverse range of natural phenomena and is fundamental to the engineering design of these systems. Flow-induced microstructure is important in materials processing, such as the production of particle-filled polymers (Migler Reference Migler2001; Elias et al. Reference Elias, Fenouillot, Majesté, Martin and Cassagnau2008; Colón Quintana et al. Reference Colón Quintana, Heckner, Chrupala, Pollock, Goris and Osswald2019), and ceramic tape casting (Jabbari et al. Reference Jabbari, Bulatova, Tok, Bahl, Mitsoulis and Hattel2016). Rheology and microstructure affect the sensation of food and digestion (Lentle & Janssen Reference Lentle and Janssen2010; Schroën, de Ruiter & Berton-Carabin Reference Schroën, de Ruiter and Berton-Carabin2020). Flow-induced demixing in polydisperse suspensions is a useful separation technique (Bandyopadhyay, Peralta-Videa & Gardea-Torresdey Reference Bandyopadhyay, Peralta-Videa and Gardea-Torresdey2013; Schroen, van Dinther & Stockmann Reference Schroen, van Dinther and Stockmann2017).
The effects of suspension microstructure are especially pronounced in tightly confined flows as arise in microfluidic devices (Van Dinther et al. Reference Van Dinther, Schroën, Vergeldt, Van der Sman and Boom2012; Sarkar & Singh Reference Sarkar and Singh2013; Dahl et al. Reference Dahl, Lin, Muller and Kumar2015; Singha et al. Reference Singha, Malipeddi, Zurita-Gotor, Sarkar, Shen, Loewenberg, Migler and Blawzdziewicz2019) and hydrofracturing (Barbati et al. Reference Barbati, Desroches, Robisson and McKinley2016; Osiptsov Reference Osiptsov2017). Blood flow in the microcirculation depends critically on the coupled rheology and flow-induced microstructure (Secomb Reference Secomb2017). The Fahraeus–Lindqvist effect refers to the concomitant reduction in haematocrit and viscosity in capillaries and small vessels (i.e. arterioles, venules). In their classical paper, Fahraeaus & Lindqvist (Reference Fahraeaus and Lindqvist1931) explain these phenomena in terms of the migration of red blood cells (erythrocytes) to the region of faster-moving fluid at the centre of the capillary where velocity gradients are smaller. This mechanism is important for reducing the workload on the heart and helps to understand the detrimental effects of certain diseased states (e.g. malaria, sickle-cell anaemia) that disrupt this mechanism by altering the mechanical properties of red blood cells (Higgins et al. Reference Higgins, Eddington, Bhatia and Mahadevan2007; Diez-Silva et al. Reference Diez-Silva, Dao, Han, Lim and Suresh2010; Chien, Gompper & Fedosov Reference Chien, Gompper and Fedosov2021). This phenomenon continues to be an active area of study (Pries, Neuhaus & Gaehtgens Reference Pries, Neuhaus and Gaehtgens1992; Tokarev, Panasenko & Ataullakhanov Reference Tokarev, Panasenko and Ataullakhanov2011; Secomb & Pries Reference Secomb and Pries2013).
Investigations of flow-induced structuring have focused on suspensions of spherical particles suspended in Newtonian liquids (Karnis, Goldsmith & Mason Reference Karnis, Goldsmith and Mason1966; Koh, Hookham & Leal Reference Koh, Hookham and Leal1994; Hampton et al. Reference Hampton, Mammoli, Graham, Tetlow and Altobelli1997; Lyon & Leal Reference Lyon and Leal1998a,Reference Lyon and Lealb). Low-Reynolds-number and large-Péclet-number conditions usually apply, based on the size of the suspended particles, the fluid viscosities and typical shear rates. Under these conditions, fluid motion is governed by the Stokes equations and Brownian motion is negligible (Duprat & Stone Reference Duprat and Stone2015). Early studies include experimental measurements (Eckstein, Bailey & Shapiro Reference Eckstein, Bailey and Shapiro1977; Leighton & Acrivos Reference Leighton and Acrivos1987a) and computer simulations (Bossis & Brady Reference Bossis and Brady1987; Chang & Powell Reference Chang and Powell1994) of self-diffusion of marked tracer particles in sheared suspensions. Eckstein et al. (Reference Eckstein, Bailey and Shapiro1977) proposed a hydrodynamic self-diffusivity, ![]() $D_s\sim \dot {\gamma } a^2$, resulting from
$D_s\sim \dot {\gamma } a^2$, resulting from ![]() $O(a)$ random particle displacements with zero mean due to uncorrelated hydrodynamic interactions between particles occurring at a rate of
$O(a)$ random particle displacements with zero mean due to uncorrelated hydrodynamic interactions between particles occurring at a rate of ![]() $\dot {\gamma }$, where
$\dot {\gamma }$, where ![]() $a$ is the particle radius,
$a$ is the particle radius, ![]() $\dot {\gamma }$ is the magnitude of the shear rate and the proportionality depends on the volume fraction. Leighton & Acrivos (Reference Leighton and Acrivos1987b) proposed the existence of a cross-flow particle flux down the particle concentration gradient with a similarly scaled hydrodynamic diffusivity,
$\dot {\gamma }$ is the magnitude of the shear rate and the proportionality depends on the volume fraction. Leighton & Acrivos (Reference Leighton and Acrivos1987b) proposed the existence of a cross-flow particle flux down the particle concentration gradient with a similarly scaled hydrodynamic diffusivity, ![]() $D\sim D_s$, and a particle drift velocity,
$D\sim D_s$, and a particle drift velocity, ![]() $V$, from high to low shear stress (Koch Reference Koch1989). The ratio of the hydrodynamic self- and gradient diffusivities to the molecular diffusivity,
$V$, from high to low shear stress (Koch Reference Koch1989). The ratio of the hydrodynamic self- and gradient diffusivities to the molecular diffusivity, ![]() $\mathcal {D}$ associated with Brownian motion, defines a Péclet number,
$\mathcal {D}$ associated with Brownian motion, defines a Péclet number, ![]() $\dot {\gamma } a^2/\mathcal {D}$; under large-Péclet-number conditions, hydrodynamic diffusion dominates Brownian diffusion (Semwogerere, Morris & Weeks Reference Semwogerere, Morris and Weeks2007).
$\dot {\gamma } a^2/\mathcal {D}$; under large-Péclet-number conditions, hydrodynamic diffusion dominates Brownian diffusion (Semwogerere, Morris & Weeks Reference Semwogerere, Morris and Weeks2007).
The Leighton & Acrivos (Reference Leighton and Acrivos1987b) theoretical framework was used to explain the anomalous time-varying viscosity previously observed by Gadala-Maria & Acrivos (Reference Gadala-Maria and Acrivos1980) (Koch Reference Koch1989) and provides the basis for the diffusive flux model of suspensions (Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992). The diffusive flux model has been subsequently used to describe the flow-induced microstructure and rheology of suspensions and emulsions (King & Leighton Reference King and Leighton2001; Ramachandran, Loewenberg & Leighton Reference Ramachandran, Loewenberg and Leighton2010; Reboucas et al. Reference Reboucas, Siqueira, Mendes and Carvalho2016). Although based on pairwise particle interactions, the diffusive flux model provides a phenomenological description for the coupled microstructure and rheology in concentrated suspensions through the use of an empirical model for the concentration-dependent shear viscosity (Eilers Reference Eilers1943; Krieger Reference Krieger1972) and transport coefficients determined from experimental data (Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992).
An alternate suspension balance model was developed where particle fluxes result from normal stress differences (Nott & Brady Reference Nott and Brady1994; Morris Reference Morris2009). The suspension balance model has also been widely used to explore the flow-induced microstructure and rheology of suspensions. The suspension balance and diffusive flux models are similar; moreover, the diffusive flux model can be derived from the suspension balance model (Nott & Brady Reference Nott and Brady1994; Nott, Guazzelli & Pouliquen Reference Nott, Guazzelli and Pouliquen2011). Both are phenomenological descriptions.
Both models have difficulty describing particle distributions at points where the local shear rate vanishes, e.g. at the centre of a Poiseuille flow, as anticipated by Leighton & Acrivos (Reference Leighton and Acrivos1987b). At these points, the predicted particle concentration profile has an unphysical singularity. The incorporation of a viscosity model in the diffusive flux model that diverges at a prescribed maximum packing fraction of particles prevents the volume fraction from diverging (Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992). However, this imposes a volume fraction equal to the prescribed maximum packing fraction at points where the shear rate vanishes which is unlikely to apply in dilute systems. The resulting cusp-shaped distribution reflects the lack of a length scale imposed by the particle size in the diffusive flux model. The use of an ad hoc non-local shear rate or a constitutive model relating stresses to velocity fluctuations rather than the local shear rate smooths the cusp that would otherwise be predicted by the suspension balance model (Morris & Brady Reference Morris and Brady1998; Frank et al. Reference Frank, Anderson, Weeks and Morris2003). Away from singular points where the shear rate vanishes, the particle concentration profiles predicted by the diffusive flux and stress balance models are in qualitative agreement with experimental measurements (Lyon & Leal Reference Lyon and Leal1998a; Frank et al. Reference Frank, Anderson, Weeks and Morris2003).
Experiments reveal size segregation in bidisperse suspensions (Husband et al. Reference Husband, Mondy, Ganani and Graham1994; Lyon & Leal Reference Lyon and Leal1998b; Semwogerere & Weeks Reference Semwogerere and Weeks2008). These studies tend to show that larger particles accumulate more quickly in regions of low shear rate. Slow evolution of the particle microstructure requires long entry lengths to attain fully developed stationary particle distributions (Nott & Brady Reference Nott and Brady1994; Phan-Thien & Fang Reference Phan-Thien and Fang1996), and experiments are often later found to have used insufficient entry lengths. Theoretical and phenomenological models are at an early stage. The diffusive flux model has been extended to bidisperse suspensions but requires more adjustable parameters (Shauly, Wachs & Nir Reference Shauly, Wachs and Nir1998; Kanehl & Stark Reference Kanehl and Stark2015; Chun et al. Reference Chun, Park, Jung and Won2019; Reddy & Singh Reference Reddy and Singh2019), and it fails at points where the shear rate vanishes, leading to predictions at odds with experiments.
Many-particle boundary integral simulations with periodic boundary conditions have been used to explore particle segregation in wall-bounded shear- and pressure-driven flows of polydisperse suspensions of deformable particles, e.g. red cells and platelets (Zhao & Shaqfeh Reference Zhao and Shaqfeh2011; Zhao, Shaqfeh & Narsimhan Reference Zhao, Shaqfeh and Narsimhan2012). These studies focused on size segregation that occurs in small channels, several particle diameters wide (e.g. arterioles, venules). The results further a fundamental understanding of the Fahraeus–Lindqvist effect and related phenomena such as plasma skimming (Tangelder et al. Reference Tangelder, Teirlinck, Slaaf and Reneman1985; Aarts et al. Reference Aarts, Van Den Broek, Prins, Kuiken, Sixma and Heethaar1988), showing that smaller, stiffer particles (platelets, and white cells) accumulate near bounding walls of a channel and larger, more deformable particles (red cells) accumulate in the central, core region of the flow (‘anti-margination’). Aside from the restriction to creeping flow conditions, which may not always apply, a drawback of boundary integral simulations is their extreme computational intensity which hinders access to the long-time stationary microstructure of these systems.
Kinetic theory models, based on the Boltzmann equation, provide another useful theoretical framework for suspension flows (Kumar & Graham Reference Kumar and Graham2012; Zurita-Gotor, Bławzdziewicz & Wajnryb Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2012; Narsimhan, Zhao & Shaqfeh Reference Narsimhan, Zhao and Shaqfeh2013; Kumar, Rivera & Graham Reference Kumar, Rivera and Graham2014; Rivera, Sinha & Graham Reference Rivera, Sinha and Graham2015; Rivera, Zhang & Graham Reference Rivera, Zhang and Graham2016; Qi & Shaqfeh Reference Qi and Shaqfeh2017, Reference Qi and Shaqfeh2018). Central to the Boltzmann equation is the particle flux generated by uncorrelated pair interactions (collisions) between particles suspended in the continuous-phase fluid. Accordingly, the Boltzmann equation is inherently a pairwise description, and thus restricted to dilute systems; however, it may provide a reasonable approximate description for particle microstructure in suspensions with moderate volume fractions. Comparisons between kinetic theory models and direct three-dimensional boundary integral simulations reveal close agreement in the predicted microstructure for volume fractions up to approximately 20 % (Narsimhan et al. Reference Narsimhan, Zhao and Shaqfeh2013; Qi & Shaqfeh Reference Qi and Shaqfeh2017, Reference Qi and Shaqfeh2018). Although they require much less computation than many-particle boundary integral simulations, kinetic theory models still require considerable computation, preventing parametric exploration of suspension microstructures. Their computational requirement is dominated by the pre-calculation of an ensemble of pair trajectories needed for evaluating the collision flux in the Boltzmann equation, but once pair trajectories are calculated, kinetic theory models provide comparatively efficient access to the long-time, statistically stationary microstructure.
For small channels, several particle diameters wide, the resulting Boltzmann equation can be numerically solved to obtain the particle distribution. Features such as margination and anti-margination are recovered (Kumar & Graham Reference Kumar and Graham2012; Zurita-Gotor et al. Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2012; Narsimhan et al. Reference Narsimhan, Zhao and Shaqfeh2013; Kumar et al. Reference Kumar, Rivera and Graham2014; Rivera et al. Reference Rivera, Sinha and Graham2015; Qi & Shaqfeh Reference Qi and Shaqfeh2017, Reference Qi and Shaqfeh2018). For channels that are wide compared with particle size, the collision flux can be expanded to yield a phenomenological particle transport equation similar to the diffusive flux model for dilute suspensions (Rivera et al. Reference Rivera, Zhang and Graham2016). Note that kinetic theory models have the same difficulty as the diffusive flux and stress balance models at points of vanishing shear rate, requiring a similar ad hoc treatment in the neighbourhood of such points (Rivera et al. Reference Rivera, Zhang and Graham2016; Qi & Shaqfeh Reference Qi and Shaqfeh2017).
Pairwise hydrodynamic interactions of force- and torque-free spherical particles in shear flow under creeping flow conditions are well understood and analytically tractable (Lin, Lee & Sather Reference Lin, Lee and Sather1970; Batchelor & Green Reference Batchelor and Green1972a,Reference Batchelor and Greenb; Zinchenko Reference Zinchenko1978, Reference Zinchenko1980, Reference Zinchenko1983). By the linearity of the Stokes equations and by symmetry, pair interactions between spherical particles on open trajectories in shear flow are reversible, yielding zero net cross-flow displacements of the particles; however, there are diverse phenomena that can break the symmetry of pair trajectories in shear flow, leading to non-zero net displacements. It is generally accepted that particle displacements resulting from irreversible pair interactions are the dominant mechanism for particle transport (Leighton & Acrivos Reference Leighton and Acrivos1987a,Reference Leighton and Acrivosb; Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992).
Mechanisms that break the symmetry of pair interactions include the perturbative effects that slightly affect hydrodynamic pair interactions and short-range phenomena that qualitatively affect the motion of particles when they are in near contact with surface-to-surface separations ![]() $h_0\ll a$ but have a negligible effect at larger separations. Short-range phenomena involve symmetry-breaking ‘contact’ interactions between particles on narrowly offset streamlines of the flow. The classical lubrication singularity between smooth spherical particles hinders the near-contact approach of particles in the compressive quadrant of the shear flow, preventing contact, and acts symmetrically slowing the separation of the particles in the extensional quadrant of the flow. Contact interactions break the symmetry of pair interactions in shear flow because they involve a compressive force that prevents particle overlap in the compressive quadrant of the flow without a compensating tensile force in the extensional quadrant.
$h_0\ll a$ but have a negligible effect at larger separations. Short-range phenomena involve symmetry-breaking ‘contact’ interactions between particles on narrowly offset streamlines of the flow. The classical lubrication singularity between smooth spherical particles hinders the near-contact approach of particles in the compressive quadrant of the shear flow, preventing contact, and acts symmetrically slowing the separation of the particles in the extensional quadrant of the flow. Contact interactions break the symmetry of pair interactions in shear flow because they involve a compressive force that prevents particle overlap in the compressive quadrant of the flow without a compensating tensile force in the extensional quadrant.
The prototypical example of a short-range mechanism for contact interactions is small-amplitude surface roughness, ![]() $d\ll a$, that prevents surface-to-surface particle separations less than
$d\ll a$, that prevents surface-to-surface particle separations less than ![]() $d$ (Smart & Leighton Reference Smart and Leighton1989; Smart, Beimfohr & Leighton Reference Smart, Beimfohr and Leighton1993; da Cunha & Hinch Reference da Cunha and Hinch1996; Rampall, Smart & Leighton Reference Rampall, Smart and Leighton1997; Wilson Reference Wilson2005; Ingber & Zinchenko Reference Ingber and Zinchenko2012). Other examples of particles with short-range contact interactions include particles with weak permeability (Reboucas & Loewenberg Reference Reboucas and Loewenberg2021a,Reference Reboucas and Loewenbergb, Reference Reboucas and Loewenberg2022), particles stabilized by screened electrostatic interactions (Zinchenko Reference Zinchenko1984; Kremer, Robbins & Grest Reference Kremer, Robbins and Grest1986) and emulsion drops under small-deformation conditions (Loewenberg & Hinch Reference Loewenberg and Hinch1997; Ramachandran et al. Reference Ramachandran, Loewenberg and Leighton2010). Particle-scale deformation associated with stronger flows is an example of a perturbative mechanism, affecting hydrodynamic interactions at
$d$ (Smart & Leighton Reference Smart and Leighton1989; Smart, Beimfohr & Leighton Reference Smart, Beimfohr and Leighton1993; da Cunha & Hinch Reference da Cunha and Hinch1996; Rampall, Smart & Leighton Reference Rampall, Smart and Leighton1997; Wilson Reference Wilson2005; Ingber & Zinchenko Reference Ingber and Zinchenko2012). Other examples of particles with short-range contact interactions include particles with weak permeability (Reboucas & Loewenberg Reference Reboucas and Loewenberg2021a,Reference Reboucas and Loewenbergb, Reference Reboucas and Loewenberg2022), particles stabilized by screened electrostatic interactions (Zinchenko Reference Zinchenko1984; Kremer, Robbins & Grest Reference Kremer, Robbins and Grest1986) and emulsion drops under small-deformation conditions (Loewenberg & Hinch Reference Loewenberg and Hinch1997; Ramachandran et al. Reference Ramachandran, Loewenberg and Leighton2010). Particle-scale deformation associated with stronger flows is an example of a perturbative mechanism, affecting hydrodynamic interactions at ![]() $O(a)$ separations, and breaking the symmetry of more distant, non-contacting pair trajectories (Lopez & Graham Reference Lopez and Graham2007; Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Singh & Sarkar Reference Singh and Sarkar2015; Malipeddi & Sarkar Reference Malipeddi and Sarkar2019a,Reference Malipeddi and Sarkarb).
$O(a)$ separations, and breaking the symmetry of more distant, non-contacting pair trajectories (Lopez & Graham Reference Lopez and Graham2007; Lac & Barthès-Biesel Reference Lac and Barthès-Biesel2008; Singh & Sarkar Reference Singh and Sarkar2015; Malipeddi & Sarkar Reference Malipeddi and Sarkar2019a,Reference Malipeddi and Sarkarb).
In this paper, we present a simplified theory for flow-induced structuring in dilute particle suspensions based on pair interactions between particles. In contrast to the phenomenological models discussed above, ours is an exact description. Starting from a Boltzmann-type master equation, particle fluxes are derived for the cross-flow hydrodynamic particle transport in flows such as shear and planar Poiseuille flow. A general analysis is presented for the boundary layer that forms in regions where the shear rate vanishes and for the stationary particle distributions that form away from these regions. Cross-stream displacements for particles that undergo symmetry breaking, contact interactions are formulated in terms of quadratures of mobility functions for spherical particles. Using this result, transport coefficients are explicitly calculated for rough particles and emulsion drops and results are presented for particle distributions in monodisperse and bidisperse suspensions.
The general formulation of the problem, including the Boltzmann equation, is presented in § 2, and expanded to derive transport coefficients including an analysis of the region where shear rates vanish. Generic results for stationary particle distributions are derived in § 3 that are independent of the character of the pair interactions between particles. Trajectories of particles that undergo contact interactions are analytically integrated in § 4 to yield particle displacements formulated as quadratures of standard mobility functions. The results from §§ 3 and 4 are combined in § 5 to obtain spatial distributions of rough particles and emulsion drops in mono- and bidisperse mixtures undergoing planar Poiseuille flow. The predictions are compared with experimental results in the literature. Concluding remarks are made in § 6.
2. Formulation of pairwise theory
2.1. Asumptions and simplifications
The starting point for our simplified theory, presented in § 2.2, is a Boltzmann-type equation for particle transport in a dilute polydisperse suspension of non-Brownian, neutrally buoyant particles undergoing unidirectional flow. Only cross-flow variations of particle concentrations are considered. Wall-induced particle migration is neglected under the assumption that the scale of the flow field is large compared with the particle size. Restricting consideration to stationary particle distributions, the collision fluxes of particle species are set to zero.
The collision flux is expanded for smoothly varying particle distributions in § 2.3 to obtain formulas for transport coefficients describing diffusive and drift fluxes of particle species driven, respectively, by gradients of particle concentrations and shear rate. The formulas are appropriately modified to handle regions with vanishing shear rate, as occurs in pressure-driven flows. The results of this section are combined in § 3 to yield an exact formulation for stationary particle distributions in dilute suspensions.
2.2. Boltzmann equation
We consider particle transport in two-dimensional unidirectional flows,
where ![]() $(X_1,X_2,X_3)$ describes a Cartesian coordinate system and
$(X_1,X_2,X_3)$ describes a Cartesian coordinate system and ![]() $\boldsymbol {e_k} (k=1,2,3)$ are the corresponding unit vectors. Velocity field (2.1) includes simple shear and planar Poiseuille flow. The particle distribution evolves in the plane perpendicular to the fluid velocity according to the Boltzmann-type equation
$\boldsymbol {e_k} (k=1,2,3)$ are the corresponding unit vectors. Velocity field (2.1) includes simple shear and planar Poiseuille flow. The particle distribution evolves in the plane perpendicular to the fluid velocity according to the Boltzmann-type equation
where ![]() $n_i(X_2,X_3)$ is the number density of type-
$n_i(X_2,X_3)$ is the number density of type-![]() $i$ particles (
$i$ particles (![]() $i=1,2,\ldots, m$). (Explicit time dependence of number density is suppressed here because we investigate stationary particle distributions.) The quantity
$i=1,2,\ldots, m$). (Explicit time dependence of number density is suppressed here because we investigate stationary particle distributions.) The quantity ![]() $F_{ik}(X_2,X_3) (k=2,3)$ is the flux of type-
$F_{ik}(X_2,X_3) (k=2,3)$ is the flux of type-![]() $i$ particles in the
$i$ particles in the ![]() $k$-direction resulting from pairwise ‘collisions’ with other particles,
$k$-direction resulting from pairwise ‘collisions’ with other particles,
 \begin{equation} F_{ik}(X_2,X_3)=\sum_{j=1}^m F_{ijk}. \end{equation}
\begin{equation} F_{ik}(X_2,X_3)=\sum_{j=1}^m F_{ijk}. \end{equation}
Here, ![]() $F_{ijk}$ is the contribution to the flux
$F_{ijk}$ is the contribution to the flux ![]() $F_{ik}$ from collisions with type-
$F_{ik}$ from collisions with type-![]() $j$ particles (
$j$ particles (![]() $j=1,2,\ldots, m$) given by the Boltzmann collision integral,
$j=1,2,\ldots, m$) given by the Boltzmann collision integral,
 \begin{equation} F_{ijk}=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\, {{\rm d}\kern0.7pt x}^{-\infty}_{2}\, {{\rm d}\kern0.7pt x}^{-\infty}_{3} \int_{-{\rm \Delta} X^{ij}_{k}}^0 n_{i}(X^{i,-\infty}_{k})n_{j}(X^{j,-\infty}_{k}) \vert {v}^{ij}\vert \, {\rm d} X^{i,-\infty}_{k}, \end{equation}
\begin{equation} F_{ijk}=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\, {{\rm d}\kern0.7pt x}^{-\infty}_{2}\, {{\rm d}\kern0.7pt x}^{-\infty}_{3} \int_{-{\rm \Delta} X^{ij}_{k}}^0 n_{i}(X^{i,-\infty}_{k})n_{j}(X^{j,-\infty}_{k}) \vert {v}^{ij}\vert \, {\rm d} X^{i,-\infty}_{k}, \end{equation}
where ![]() $X^{i,-\infty }_{k} (k=2,3)$ is the initial distance of particle
$X^{i,-\infty }_{k} (k=2,3)$ is the initial distance of particle ![]() $i$ from the plane
$i$ from the plane ![]() $X_{k}$ where the flux is evaluated,
$X_{k}$ where the flux is evaluated, ![]() ${\rm \Delta} X^{ij}_{k}$ is the displacement of particle
${\rm \Delta} X^{ij}_{k}$ is the displacement of particle ![]() $i$ in the
$i$ in the ![]() $k$-direction due to its binary encounter with particle
$k$-direction due to its binary encounter with particle ![]() $j$, and
$j$, and
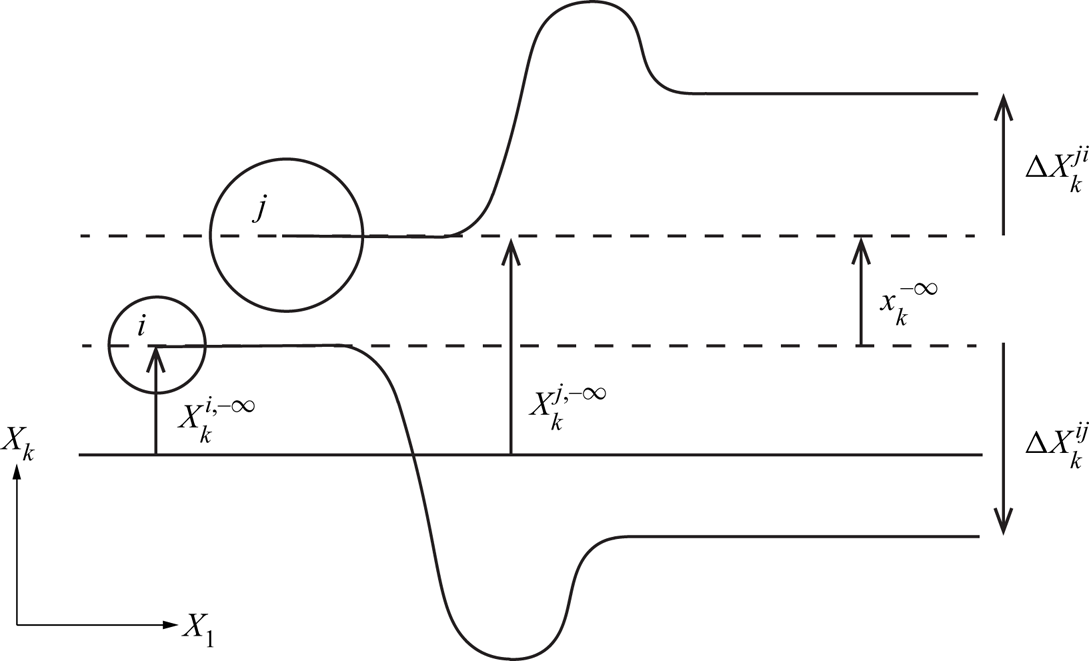
is the relative initial position of the particles in the cross-flow plane, i.e. the trajectory offset, as shown in figure 1. Here, ![]() $\vert {v}^{ij} \vert$ is the magnitude of the relative velocity between widely separated particles,
$\vert {v}^{ij} \vert$ is the magnitude of the relative velocity between widely separated particles,
and ![]() ${v}(X_2)$ is the prescribed velocity (2.1). Prior to a pair interaction, particles are widely separated in the
${v}(X_2)$ is the prescribed velocity (2.1). Prior to a pair interaction, particles are widely separated in the ![]() $X_1$-direction (i.e. flow direction) with uncorrelated initial positions
$X_1$-direction (i.e. flow direction) with uncorrelated initial positions ![]() $(X^{i,-\infty }_{2}, X^{i,-\infty }_{3})$ and
$(X^{i,-\infty }_{2}, X^{i,-\infty }_{3})$ and ![]() $(X^{j,-\infty }_{2}, X^{j,-\infty }_{3})$ in the cross-flow plane.
$(X^{j,-\infty }_{2}, X^{j,-\infty }_{3})$ in the cross-flow plane.

Figure 1. Schematic showing trajectories of particles undergoing pair interaction projected on the 1–![]() $k$ plane (
$k$ plane (![]() $k=2,3$); cross-flow displacements
$k=2,3$); cross-flow displacements ![]() ${\rm \Delta} X^{ij}_k$ and
${\rm \Delta} X^{ij}_k$ and ![]() ${\rm \Delta} X^{ji}_k$ of particles
${\rm \Delta} X^{ji}_k$ of particles ![]() $i$ and
$i$ and ![]() $j$, respectively;
$j$, respectively; ![]() $X^{i,-\infty }_k$ and
$X^{i,-\infty }_k$ and ![]() $X^{j,-\infty }_k$ are coordinates of the particles in cross-flow plane (
$X^{j,-\infty }_k$ are coordinates of the particles in cross-flow plane (![]() $X_2,X_3$) prior to interaction (dashed lines) and
$X_2,X_3$) prior to interaction (dashed lines) and ![]() $x^{-\infty }_{k}=X^{j,-\infty }_{k}-X^{i,-\infty }_{k}$ is the initial trajectory offset; particle flux is evaluated at plane of constant
$x^{-\infty }_{k}=X^{j,-\infty }_{k}-X^{i,-\infty }_{k}$ is the initial trajectory offset; particle flux is evaluated at plane of constant ![]() $X_k$ (solid line).
$X_k$ (solid line).
Formula (2.4) is obtained using the odd symmetry of particle displacements with respect to trajectory offset,
for ![]() $(k=2,3)$. Particle displacements are, moreover, symmetric with respect to complementary coordinates, i.e.
$(k=2,3)$. Particle displacements are, moreover, symmetric with respect to complementary coordinates, i.e.
Cross-flow convection due to particle migration away from solid boundaries is omitted from (2.2) under the assumption that flow occurs in a channel that is wide compared with particle size. In the absence of wall interactions that can produce cross-swapping trajectories (Zurita-Gotor et al. Reference Zurita-Gotor, Bławzdziewicz and Wajnryb2012; Reddig & Stark Reference Reddig and Stark2013), particle displacements obey the relation
The equality holds only for ![]() $x^{-\infty }_{k}=0$ and for widely separated particles.
$x^{-\infty }_{k}=0$ and for widely separated particles.
2.2.1. Boundary conditions
Stationary particle distributions are governed by
under the assumption that the channel walls are impermeable to the particles. In channel flows, a bulk number density, ![]() $n_{i\infty }$, can be imposed for each particle type
$n_{i\infty }$, can be imposed for each particle type ![]() $(i=1,2,\ldots,m)$,
$(i=1,2,\ldots,m)$,
where ![]() $q$ is the volume flow through a channel with cross-section
$q$ is the volume flow through a channel with cross-section ![]() $S_\perp$.
$S_\perp$.
Diluteness requires low volume fractions,
where number densities are related to volume fractions, ![]() $\phi _i=n_i {v}_i$, and
$\phi _i=n_i {v}_i$, and ![]() ${v}_i$ is particle volume. Stationary particle distributions depend nonlinearly on the bulk composition
${v}_i$ is particle volume. Stationary particle distributions depend nonlinearly on the bulk composition ![]() $n_{i\infty }/n_\infty$ given that the particle flux (2.4) is quadratic in number density. However, the total bulk density
$n_{i\infty }/n_\infty$ given that the particle flux (2.4) is quadratic in number density. However, the total bulk density ![]() $n_\infty =\sum _{i=1}^m n_{i\infty }$ can be scaled out of (2.10) and (2.11). Stationary particle density distributions are proportional to the total bulk number density.
$n_\infty =\sum _{i=1}^m n_{i\infty }$ can be scaled out of (2.10) and (2.11). Stationary particle density distributions are proportional to the total bulk number density.
2.3. Particle transport
2.3.1. Local transport coefficients
Here, we analyse particle transport in suspensions undergoing flows with velocity (2.1) and derive diffusive and drift fluxes, i.e. fluxes proportional to the local concentration gradients of particle species and a flux associated with a drift velocity of particles from high to low shear rates. Local transport coefficients for these fluxes are obtained. The diffusive fluxes have been derived previously (Zarraga & Leighton Reference Zarraga and Leighton2001) and a drift velocity has been extracted from a Boltzmann collision integral (Rivera et al. Reference Rivera, Zhang and Graham2016). A brief derivation is provided below for completeness and uniformity.
The diffusive and drift fluxes are obtained by evaluating the collision flux (2.4) for perturbative variations in number densities and relative velocities. The number densities and shear rates are expanded up to linear variations
 \begin{gather} n_i=n_{i 0}+\sum_{k=2}^{3} \frac{\partial n_i}{\partial X_k}X_k+O(X^2_k), \end{gather}
\begin{gather} n_i=n_{i 0}+\sum_{k=2}^{3} \frac{\partial n_i}{\partial X_k}X_k+O(X^2_k), \end{gather}
where ![]() $\dot {\gamma }_0$ and
$\dot {\gamma }_0$ and ![]() $n_{i 0}$, respectively, are the local shear-rate magnitude and number densities of the particles at
$n_{i 0}$, respectively, are the local shear-rate magnitude and number densities of the particles at ![]() $X_k=0$ (
$X_k=0$ (![]() $k=2,3$); the quantities
$k=2,3$); the quantities ![]() $d\dot {\gamma }/d X_2$ and
$d\dot {\gamma }/d X_2$ and ![]() $\partial n_i/\partial X_k$ are the corresponding local values of the derivatives. Brownian motion is neglected under the assumption of large Péclet number
$\partial n_i/\partial X_k$ are the corresponding local values of the derivatives. Brownian motion is neglected under the assumption of large Péclet number
where ![]() $\mathcal {D}$ is the molecular diffusivity. In general, the relative velocity (2.6) becomes
$\mathcal {D}$ is the molecular diffusivity. In general, the relative velocity (2.6) becomes
The development presented in this section assumes a non-vanishing shear rate
so that the relative velocity (2.16) reduces to
The case of vanishing shear rates is analysed in the next section.
Inserting (2.13) and (2.14) into the flux (2.4) and integrating in ![]() $X_{k}^{i,-\infty }$ yields the net flux of type-
$X_{k}^{i,-\infty }$ yields the net flux of type-![]() $i$ particles,
$i$ particles,
where ![]() $F^{(c)}_{ik}$ are the diffusive fluxes
$F^{(c)}_{ik}$ are the diffusive fluxes
 \begin{equation} F^{(c)}_{ik}={-}D_{ik}^{s}\frac{{\rm d} n_{i}}{{\rm d} X_{k}}- \sum_{j=1}^m\left( D_{ijk}\frac{{\rm d} n_{j}}{{\rm d} X_{k}}\right), \end{equation}
\begin{equation} F^{(c)}_{ik}={-}D_{ik}^{s}\frac{{\rm d} n_{i}}{{\rm d} X_{k}}- \sum_{j=1}^m\left( D_{ijk}\frac{{\rm d} n_{j}}{{\rm d} X_{k}}\right), \end{equation}
and ![]() $F^{(\dot {\gamma })}_{i2}$ is the drift flux
$F^{(\dot {\gamma })}_{i2}$ is the drift flux
The Kronecker delta ![]() $\delta _{pq}$ in (2.19) indicates that there is a drift flux in the
$\delta _{pq}$ in (2.19) indicates that there is a drift flux in the ![]() $X_2-$direction only.
$X_2-$direction only.
The above diffusivities and the drift-velocity coefficient are defined by
 \begin{gather} D_{ik}^{s}=\dot{\gamma}_0\sum_{j=1}^m n_{j0} I^{A}_{ijk}, \end{gather}
\begin{gather} D_{ik}^{s}=\dot{\gamma}_0\sum_{j=1}^m n_{j0} I^{A}_{ijk}, \end{gather} \begin{gather}V_{i}=\sum_{j=1}^m n_{j0} \left(I^{A}_{ij2}+ \frac{1}{2}I^{B}_{ij2}\right), \end{gather}
\begin{gather}V_{i}=\sum_{j=1}^m n_{j0} \left(I^{A}_{ij2}+ \frac{1}{2}I^{B}_{ij2}\right), \end{gather}
where ![]() $I^A_{ijk}$,
$I^A_{ijk}$, ![]() $I^B_{ijk}$ are integrals over the relative cross-flow-plane coordinates (2.5)
$I^B_{ijk}$ are integrals over the relative cross-flow-plane coordinates (2.5)
Both integrals are intrinsically positive given the symmetry (2.8a,b) and sign of particle displacements (2.9).
The self-diffusivity of type-![]() $i$ particles,
$i$ particles, ![]() $D_{ik}^{s}$, defined by (2.22), can be directly obtained as a sum of the rate of mean squared displacements from random encounters with all particle species. Diffusive fluxes occur in both the velocity gradient and vorticity directions and have contributions from concentration gradients of all species; a non-zero diffusive flux of a species with uniform concentration can be generated by a gradient of another species. This formulation of the diffusive fluxes concurs with that presented by Zarraga & Leighton (Reference Zarraga and Leighton2001).
$D_{ik}^{s}$, defined by (2.22), can be directly obtained as a sum of the rate of mean squared displacements from random encounters with all particle species. Diffusive fluxes occur in both the velocity gradient and vorticity directions and have contributions from concentration gradients of all species; a non-zero diffusive flux of a species with uniform concentration can be generated by a gradient of another species. This formulation of the diffusive fluxes concurs with that presented by Zarraga & Leighton (Reference Zarraga and Leighton2001).
The drift velocities describe the migration of particles from regions of high shear rates. Gradients of the shear-rate magnitude ![]() $\dot {\gamma }$ generate an oppositely directed flux. By symmetry, gradients of the shear-rate magnitude do not contribute to the diffusive flux.
$\dot {\gamma }$ generate an oppositely directed flux. By symmetry, gradients of the shear-rate magnitude do not contribute to the diffusive flux.
The ![]() $O(r^{-3})$ far-field velocity gradients of force-free particles perturb the trajectories of deformable particles, where
$O(r^{-3})$ far-field velocity gradients of force-free particles perturb the trajectories of deformable particles, where ![]() $r$ is distance between the particles normalized by particle size. Integrated along an open trajectory, this perturbation produces pair displacements
$r$ is distance between the particles normalized by particle size. Integrated along an open trajectory, this perturbation produces pair displacements ![]() ${\rm \Delta} X_k^{ij}=O(r^{-\infty })^{-2}$ for widely offset trajectories,
${\rm \Delta} X_k^{ij}=O(r^{-\infty })^{-2}$ for widely offset trajectories, ![]() $r^{-\infty } \gg 1$, where
$r^{-\infty } \gg 1$, where ![]() $r^{-\infty }$ is the radial relative trajectory coordinate, defined in figure 2. Accordingly, integral (2.26) is divergent. The self-diffusivity of deformable particles can be computed from pair interactions because integral (2.25) converges (Loewenberg & Hinch Reference Loewenberg and Hinch1997), but the evaluation of the diffusive and drift fluxes (2.20) and (2.21) requires a numerical cutoff,
$r^{-\infty }$ is the radial relative trajectory coordinate, defined in figure 2. Accordingly, integral (2.26) is divergent. The self-diffusivity of deformable particles can be computed from pair interactions because integral (2.25) converges (Loewenberg & Hinch Reference Loewenberg and Hinch1997), but the evaluation of the diffusive and drift fluxes (2.20) and (2.21) requires a numerical cutoff, ![]() $r_c^{ij}=r_c^{ji}$, a trajectory offset beyond which interactions between type-
$r_c^{ij}=r_c^{ji}$, a trajectory offset beyond which interactions between type-![]() $i$ and type-
$i$ and type-![]() $j$ particles cause cross-flow displacements, i.e.
$j$ particles cause cross-flow displacements, i.e.

Figure 2. Cylindrical coordinate system ![]() $(r^{-\infty }, \theta )$ for the cross-flow plane
$(r^{-\infty }, \theta )$ for the cross-flow plane ![]() $(x_3^{-\infty }, x_2^{-\infty })$, where
$(x_3^{-\infty }, x_2^{-\infty })$, where ![]() $x_3^{-\infty }=r^{-\infty }\cos \theta$ and
$x_3^{-\infty }=r^{-\infty }\cos \theta$ and ![]() $x_2^{-\infty }=r^{-\infty }\sin \theta$.
$x_2^{-\infty }=r^{-\infty }\sin \theta$.
With this cutoff, integrals (2.25) and (2.26) become
 \begin{gather} I^{A}_{ijk}=\frac{1}{2}\int_0^{2{\rm \pi}} \int^{r_c^{ij}}_{0}\vert r^{-\infty}\sin\theta\vert ({\rm \Delta} X^{ij}_{k})^2 r^{-\infty}\, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{gather}
\begin{gather} I^{A}_{ijk}=\frac{1}{2}\int_0^{2{\rm \pi}} \int^{r_c^{ij}}_{0}\vert r^{-\infty}\sin\theta\vert ({\rm \Delta} X^{ij}_{k})^2 r^{-\infty}\, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{gather} \begin{gather}I^{B}_{ijk}={-}\int_0^{2{\rm \pi}} \int^{r_c^{ij}}_{0}|r^{-\infty}\sin\theta |x^{-\infty}_{k} {\rm \Delta} X^{ij}_{k} \, r^{-\infty}\, {\rm d} r^{-\infty} \, {\rm d} \theta, \end{gather}
\begin{gather}I^{B}_{ijk}={-}\int_0^{2{\rm \pi}} \int^{r_c^{ij}}_{0}|r^{-\infty}\sin\theta |x^{-\infty}_{k} {\rm \Delta} X^{ij}_{k} \, r^{-\infty}\, {\rm d} r^{-\infty} \, {\rm d} \theta, \end{gather}
where ![]() $(r^{-\infty }, \theta )$ is the cylindrical coordinate system shown in figure 2 and
$(r^{-\infty }, \theta )$ is the cylindrical coordinate system shown in figure 2 and ![]() $x^{-\infty }_{k}$ is defined in the caption.
$x^{-\infty }_{k}$ is defined in the caption.
In general, truncation of the integration domain is an ad hoc procedure, and results depend on ![]() $r_c^{ij}$ (Narsimhan et al. Reference Narsimhan, Zhao and Shaqfeh2013). However, boundary condition (2.27a,b) applies rigorously for spherical particles that undergo contact interactions, as discussed in § 4. Such particles have circular upstream collision cross-sections
$r_c^{ij}$ (Narsimhan et al. Reference Narsimhan, Zhao and Shaqfeh2013). However, boundary condition (2.27a,b) applies rigorously for spherical particles that undergo contact interactions, as discussed in § 4. Such particles have circular upstream collision cross-sections ![]() $r_c^{ij}$ that scale with particle size (Zinchenko Reference Zinchenko1984; da Cunha & Hinch Reference da Cunha and Hinch1996).
$r_c^{ij}$ that scale with particle size (Zinchenko Reference Zinchenko1984; da Cunha & Hinch Reference da Cunha and Hinch1996).
2.3.2. Particle transport at points of vanishing shear rate
Here, the analysis of particle transport developed in the previous section is extended to regions where the shear rate vanishes linearly. Accordingly, we consider regions where the velocity is locally quadratic,
where ![]() $\gamma '_2$ is the magnitude of the shear-rate gradient and
$\gamma '_2$ is the magnitude of the shear-rate gradient and ![]() ${v}_0$ is an arbitrary local velocity that can be ignored since only velocity differences are significant. The corresponding magnitude of the shear rate and its gradient are given by
${v}_0$ is an arbitrary local velocity that can be ignored since only velocity differences are significant. The corresponding magnitude of the shear rate and its gradient are given by
An example is the velocity field at the centre of planar Poiseuille flow in a channel of half-width ![]() $H$, where
$H$, where ![]() $\boldsymbol {v}$ is given by (2.1) with
$\boldsymbol {v}$ is given by (2.1) with
 \begin{equation} {v}={v}_0\left[1-\left(\frac{X_{2}}{H}\right)^2\right]. \end{equation}
\begin{equation} {v}={v}_0\left[1-\left(\frac{X_{2}}{H}\right)^2\right]. \end{equation}
Here, ![]() ${v}_0$ is the velocity at centreline,
${v}_0$ is the velocity at centreline, ![]() $X_2=0$, and the magnitude of the shear rate is given by (2.31a,b) with
$X_2=0$, and the magnitude of the shear rate is given by (2.31a,b) with ![]() $\gamma '_2=2{v}_0 H^{-2}$. Neglecting Brownian motion in regions where the shear rate vanishes requires a more stringent condition; in this case, requirement (2.15) is replaced by
$\gamma '_2=2{v}_0 H^{-2}$. Neglecting Brownian motion in regions where the shear rate vanishes requires a more stringent condition; in this case, requirement (2.15) is replaced by
Inserting (2.31a,b) into (2.16) yields the relative velocity magnitude,
For ![]() $\lvert X_2\rvert > X_c^{ij}$, the result reduces to the form of (2.18),
$\lvert X_2\rvert > X_c^{ij}$, the result reduces to the form of (2.18),
where ![]() $X_c^{ij}$ is an upper bound of the excluded region
$X_c^{ij}$ is an upper bound of the excluded region ![]() $\vert X^{i,-\infty }_{2}+\frac {1}{2}x^{-\infty }_{2}\vert$. Here,
$\vert X^{i,-\infty }_{2}+\frac {1}{2}x^{-\infty }_{2}\vert$. Here, ![]() $X_c^{ij}$ is given by
$X_c^{ij}$ is given by
where ![]() ${\rm \Delta} X^{ij}_{2, {max}}$ is the maximum displacement magnitude of a type-
${\rm \Delta} X^{ij}_{2, {max}}$ is the maximum displacement magnitude of a type-![]() $i$ particle by a pair interaction with a type-
$i$ particle by a pair interaction with a type-![]() $j$ particle and is thus the upper bound for
$j$ particle and is thus the upper bound for ![]() $\vert X^{i,-\infty }_{2}\vert$; the radius of the collision cross-section,
$\vert X^{i,-\infty }_{2}\vert$; the radius of the collision cross-section, ![]() $r_c^{ij}$, defined by (2.27a,b), is the upper bound for
$r_c^{ij}$, defined by (2.27a,b), is the upper bound for ![]() $\lvert x_2^{-\infty }\rvert$. In general,
$\lvert x_2^{-\infty }\rvert$. In general, ![]() ${\rm \Delta} X^{ij}_{2, {max}}$, and thus
${\rm \Delta} X^{ij}_{2, {max}}$, and thus ![]() $X_c^{ij}$, are
$X_c^{ij}$, are ![]() $O(r_c^{ij})$. For spherical particles that undergo contact interactions,
$O(r_c^{ij})$. For spherical particles that undergo contact interactions, ![]() $X_c^{ij} \leq r_c^{ij}$, as discussed in § 4.
$X_c^{ij} \leq r_c^{ij}$, as discussed in § 4.
For ![]() $\lvert X_2\rvert > X_c^{ij}$, the local analysis presented in § 2.3.1 applies with shear-rate magnitude and gradient given by (2.31a,b). Accordingly, a linearly varying diffusive flux and constant drift velocity are obtained according to (2.20)–(2.24). However, for
$\lvert X_2\rvert > X_c^{ij}$, the local analysis presented in § 2.3.1 applies with shear-rate magnitude and gradient given by (2.31a,b). Accordingly, a linearly varying diffusive flux and constant drift velocity are obtained according to (2.20)–(2.24). However, for ![]() $\lvert X_2\rvert < X_c^{ij}$, the relative velocity,
$\lvert X_2\rvert < X_c^{ij}$, the relative velocity, ![]() ${v}_{ij}$, changes sign within the maximum range of particle displacements,
${v}_{ij}$, changes sign within the maximum range of particle displacements, ![]() ${\rm \Delta} X^{ij}_{2, {max}}$, that contribute to the particle flux. Within this region, (2.34) must be used to describe the magnitude of the relative velocity. The use of (2.35) is inconsistent and leads to incorrect results. For example, inserting the linearly varying diffusive flux balanced by the constant drift velocity, obtained by the local analysis (2.22)–(2.24) into (2.19) and then (2.10) yields,
${\rm \Delta} X^{ij}_{2, {max}}$, that contribute to the particle flux. Within this region, (2.34) must be used to describe the magnitude of the relative velocity. The use of (2.35) is inconsistent and leads to incorrect results. For example, inserting the linearly varying diffusive flux balanced by the constant drift velocity, obtained by the local analysis (2.22)–(2.24) into (2.19) and then (2.10) yields,
where ![]() $M_1$ is a positive constant. A singular distribution,
$M_1$ is a positive constant. A singular distribution, ![]() $n\approx \lvert X_2\vert ^{-M_1}$ is thus obtained, as pointed out by Leighton & Acrivos (Reference Leighton and Acrivos1987b).
$n\approx \lvert X_2\vert ^{-M_1}$ is thus obtained, as pointed out by Leighton & Acrivos (Reference Leighton and Acrivos1987b).
The region ![]() $\lvert X_2\rvert < X_c^{ij}$ defines a boundary layer within which the transport coefficients exhibit a more complex dependence on position
$\lvert X_2\rvert < X_c^{ij}$ defines a boundary layer within which the transport coefficients exhibit a more complex dependence on position ![]() $X_2$. By retaining the relative velocity magnitude (2.34) in this region, we obtain the essential dependence of the transport coefficients required to avoid the spurious singularity at
$X_2$. By retaining the relative velocity magnitude (2.34) in this region, we obtain the essential dependence of the transport coefficients required to avoid the spurious singularity at ![]() $X_2=0$ without the need for any of the ad hoc manoeuvres used in prior studies, as discussed in the introduction.
$X_2=0$ without the need for any of the ad hoc manoeuvres used in prior studies, as discussed in the introduction.
Particle transport in the vorticity direction (![]() $k=3$) does not have a singular behaviour because there is no drift velocity, so the local analysis presented in § 2.3.1 is uniformly valid.
$k=3$) does not have a singular behaviour because there is no drift velocity, so the local analysis presented in § 2.3.1 is uniformly valid.
According to the derivation provided in Appendix A, the particle flux in the velocity-gradient direction is given by
where the diffusive and drift fluxes are
 \begin{gather} F^{(c)}_{i2}(X_2)={-}D_{i2}^{s}(X_2)\frac{{\rm d} n_{i}}{{\rm d} X_{2}}-\sum_{j=1}^m\left( D_{ij2}(X_2) \frac{{\rm d} n_{j}}{{\rm d} X_{2}}\right), \end{gather}
\begin{gather} F^{(c)}_{i2}(X_2)={-}D_{i2}^{s}(X_2)\frac{{\rm d} n_{i}}{{\rm d} X_{2}}-\sum_{j=1}^m\left( D_{ij2}(X_2) \frac{{\rm d} n_{j}}{{\rm d} X_{2}}\right), \end{gather}the diffusivities and drift-velocity coefficient are
 \begin{gather} D^{s}_{i2}(X_2)=\gamma'_2\lvert X_2\rvert \sum_{j=1}^{m} n_{j0} I_{ij}^{(1)}(X_2) , \end{gather}
\begin{gather} D^{s}_{i2}(X_2)=\gamma'_2\lvert X_2\rvert \sum_{j=1}^{m} n_{j0} I_{ij}^{(1)}(X_2) , \end{gather} \begin{gather}V_{i}(X_2)=\sum_{j=1}^m n_{j0} I^{(3)}_{ij}(X_2). \end{gather}
\begin{gather}V_{i}(X_2)=\sum_{j=1}^m n_{j0} I^{(3)}_{ij}(X_2). \end{gather}
Following the analysis presented in Appendix A, integrals ![]() $I_{ij}^{(1)}, I_{ij}^{(2)}, I_{ij}^{(3)}$ are given by
$I_{ij}^{(1)}, I_{ij}^{(2)}, I_{ij}^{(3)}$ are given by
 \begin{align} I_{ij}^{(1)}(X_2)&=\frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int^{r_c^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{2} \vert X_2\vert ({\rm \Delta} X^{ij}_{2})^2 B^2(X_2') +\frac{1}{3} (-{\rm \Delta} X^{ij}_{2})^3(1-B^3(X'_{2})) \right. \nonumber\\ & \quad \left. + \frac{1}{4} r^{-\infty} \sin \theta ({\rm \Delta} X^{ij}_{2})^2 (1-B^2(X'_{2})) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta ,\end{align}
\begin{align} I_{ij}^{(1)}(X_2)&=\frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int^{r_c^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{2} \vert X_2\vert ({\rm \Delta} X^{ij}_{2})^2 B^2(X_2') +\frac{1}{3} (-{\rm \Delta} X^{ij}_{2})^3(1-B^3(X'_{2})) \right. \nonumber\\ & \quad \left. + \frac{1}{4} r^{-\infty} \sin \theta ({\rm \Delta} X^{ij}_{2})^2 (1-B^2(X'_{2})) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta ,\end{align} \begin{align} I_{ij}^{(2)}(X_2)&=\frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta \left[ r^{-\infty} \sin \theta \vert X_2\vert (-{\rm \Delta} X^{ij}_{2}) B(X'_{2})+\frac{1}{2}\vert X_2\vert ({\rm \Delta} X^{ij}_{2})^2 B^2(X'_{2}) \right. \nonumber\\ & \quad \left. +\frac{1}{3}(-{\rm \Delta} X^{ij}_{2})^3(1-B^3(X'_{2})) + \frac{3}{4} r^{-\infty} \sin \theta ({\rm \Delta} X^{ij}_{2})^2 (1-B^2(X'_{2})) \right. \nonumber\\ & \quad \left. +\frac{1}{2}(r^{-\infty} \sin \theta)^2 (-{\rm \Delta} X^{ij}_{2})(1-B(X'_{2})) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
\begin{align} I_{ij}^{(2)}(X_2)&=\frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta \left[ r^{-\infty} \sin \theta \vert X_2\vert (-{\rm \Delta} X^{ij}_{2}) B(X'_{2})+\frac{1}{2}\vert X_2\vert ({\rm \Delta} X^{ij}_{2})^2 B^2(X'_{2}) \right. \nonumber\\ & \quad \left. +\frac{1}{3}(-{\rm \Delta} X^{ij}_{2})^3(1-B^3(X'_{2})) + \frac{3}{4} r^{-\infty} \sin \theta ({\rm \Delta} X^{ij}_{2})^2 (1-B^2(X'_{2})) \right. \nonumber\\ & \quad \left. +\frac{1}{2}(r^{-\infty} \sin \theta)^2 (-{\rm \Delta} X^{ij}_{2})(1-B(X'_{2})) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}and
 \begin{align} I_{ij}^{(3)}(X_2)&= \mbox{sign}(X_2)\, \int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{2}({\rm \Delta} X^{ij}_{2})^2 B^2(X'_{2})+ \frac{1}{2} r^{-\infty}\sin \theta (-{\rm \Delta} X^{ij}_{2}) B(X'_{2}) \right. \nonumber\\ &\quad \left. \vphantom{\frac{1}{2}}+\vert X_2\vert(-{\rm \Delta} X^{ij}_{2}) (1-B(X'_{2})) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
\begin{align} I_{ij}^{(3)}(X_2)&= \mbox{sign}(X_2)\, \int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{2}({\rm \Delta} X^{ij}_{2})^2 B^2(X'_{2})+ \frac{1}{2} r^{-\infty}\sin \theta (-{\rm \Delta} X^{ij}_{2}) B(X'_{2}) \right. \nonumber\\ &\quad \left. \vphantom{\frac{1}{2}}+\vert X_2\vert(-{\rm \Delta} X^{ij}_{2}) (1-B(X'_{2})) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
where ![]() $(r^{-\infty },\theta )$ are the cylindrical coordinates defined in figure 2, and
$(r^{-\infty },\theta )$ are the cylindrical coordinates defined in figure 2, and
 \begin{equation} X_2'= \frac{\vert X_2\vert-\frac{1}{2}r^{-\infty}\sin\theta}{-{\rm \Delta} X^{ij}_{2}}. \end{equation}
\begin{equation} X_2'= \frac{\vert X_2\vert-\frac{1}{2}r^{-\infty}\sin\theta}{-{\rm \Delta} X^{ij}_{2}}. \end{equation}
Here, ![]() $B(t)$ is the ramp function sketched in figure 3 and defined by
$B(t)$ is the ramp function sketched in figure 3 and defined by
where ![]() $\varTheta (t)$ is the Heaviside function. Note that
$\varTheta (t)$ is the Heaviside function. Note that
by (2.9) and the remark below it. It follows that integrals (2.44)–(2.46), and thus the transport coefficients (2.41)–(2.43), are positive provided ![]() $X_2\neq 0$.
$X_2\neq 0$.

Figure 3. Ramp function defined by (2.48).
2.3.3. Discussion
Here, we point out the salient features of the diffusive and drift fluxes in the boundary-layer region.
For ![]() $\lvert X_2\rvert \geq X_c^{ij}$, we have
$\lvert X_2\rvert \geq X_c^{ij}$, we have ![]() $X_2'\geq 1$, according to (2.36) and (2.47), and thus
$X_2'\geq 1$, according to (2.36) and (2.47), and thus
Inserting this result into integrals (2.44)–(2.46) reduces them to their local forms
Accordingly, the transport coefficients (2.41)–(2.43) reduce to their corresponding local forms, (2.22)–(2.24), with the shear-rate magnitude and its gradient given by (2.31a,b).
First-derivative discontinuities introduced by the ramp function (2.48) are manifest by second-derivative discontinuities of integrals ![]() $I^{(k)}_{ij}(X_2)$ (
$I^{(k)}_{ij}(X_2)$ (![]() $k=1,2,3$) and the transport coefficients (2.41)–(2.43) at
$k=1,2,3$) and the transport coefficients (2.41)–(2.43) at ![]() $\lvert X_2\rvert =X_c^{ij}$. The source of these discontinuities is the discrete interaction range (2.27a,b) for contact interactions between spherical particles.
$\lvert X_2\rvert =X_c^{ij}$. The source of these discontinuities is the discrete interaction range (2.27a,b) for contact interactions between spherical particles.
According to (2.44)–(2.46), integrals ![]() $I^{(1)}(X_2)$ and
$I^{(1)}(X_2)$ and ![]() $I^{(2)}(X_2)$ are even functions of
$I^{(2)}(X_2)$ are even functions of ![]() $X_2$ and
$X_2$ and ![]() $I^{(3)}(X_2)$ is an odd function. (This is plainly seen in the antecedent (A2)–(A4).) Thus, diffusivities (2.41)–(2.42) are even functions and drift velocities (2.43) are odd functions of
$I^{(3)}(X_2)$ is an odd function. (This is plainly seen in the antecedent (A2)–(A4).) Thus, diffusivities (2.41)–(2.42) are even functions and drift velocities (2.43) are odd functions of ![]() $X_2$. Near the centreline, integrals (2.44)–(2.46) reduce to
$X_2$. Near the centreline, integrals (2.44)–(2.46) reduce to
 \begin{align} \lim_{X_2\to 0}\lvert X_2\rvert I_{ij}^{(1)}(X_2)&=\int_{0}^{\rm \pi} \int^{r_c^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{3} (-{\rm \Delta} X^{ij}_{2})^3 \right. \nonumber\\ & \quad \left. + \frac{1}{4} r^{-\infty} \sin \theta\, ({\rm \Delta} X^{ij}_{2})^2\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
\begin{align} \lim_{X_2\to 0}\lvert X_2\rvert I_{ij}^{(1)}(X_2)&=\int_{0}^{\rm \pi} \int^{r_c^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{3} (-{\rm \Delta} X^{ij}_{2})^3 \right. \nonumber\\ & \quad \left. + \frac{1}{4} r^{-\infty} \sin \theta\, ({\rm \Delta} X^{ij}_{2})^2\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align} \begin{align} \lim_{X_2\to 0}\lvert X_2\rvert I_{ij}^{(2)}(X_2)&=\int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{3}(-{\rm \Delta} X^{ij}_{2})^3 \right. \nonumber\\ & \quad \left. + \frac{3}{4} r^{-\infty} \sin \theta ({\rm \Delta} X^{ij}_{2})^2 +\frac{1}{2}(r^{-\infty} \sin \theta)^2 (-{\rm \Delta} X^{ij}_{2}) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
\begin{align} \lim_{X_2\to 0}\lvert X_2\rvert I_{ij}^{(2)}(X_2)&=\int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta \left[ \frac{1}{3}(-{\rm \Delta} X^{ij}_{2})^3 \right. \nonumber\\ & \quad \left. + \frac{3}{4} r^{-\infty} \sin \theta ({\rm \Delta} X^{ij}_{2})^2 +\frac{1}{2}(r^{-\infty} \sin \theta)^2 (-{\rm \Delta} X^{ij}_{2}) \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}and
 \begin{equation} \lim_{X_2\to 0} I_{ij}^{(3)}(X_2)= X_2\, \int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta(-{\rm \Delta} X^{ij}_{2}) r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta . \end{equation}
\begin{equation} \lim_{X_2\to 0} I_{ij}^{(3)}(X_2)= X_2\, \int_{0}^{\rm \pi} \int^{r_{c}^{ij}}_{0} r^{-\infty}\sin \theta(-{\rm \Delta} X^{ij}_{2}) r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta . \end{equation}
Inserting these results with (2.49) into (2.41)–(2.43) shows that diffusivities are finite and positive and drift velocities are linear with positive slope for ![]() $X_2\to 0$. Inserting these results into (2.38) and (2.10) indicates that particle transport near the centreline is governed by
$X_2\to 0$. Inserting these results into (2.38) and (2.10) indicates that particle transport near the centreline is governed by
where ![]() $M_2$ is a positive constant, and
$M_2$ is a positive constant, and ![]() $y=X_2/X_c^{ij}$ is a dimensionless length variable. By contrast to (2.37), this equation predicts the smooth, non-singular behaviour,
$y=X_2/X_c^{ij}$ is a dimensionless length variable. By contrast to (2.37), this equation predicts the smooth, non-singular behaviour, ![]() $n\approx n_0(1- \frac {1}{2} M_2\, y^2)$, where
$n\approx n_0(1- \frac {1}{2} M_2\, y^2)$, where ![]() $n_0$ is the number density at
$n_0$ is the number density at ![]() $y=0$. Hence, the source of the classical singular particle distribution, described above, is eliminated. Note that
$y=0$. Hence, the source of the classical singular particle distribution, described above, is eliminated. Note that ![]() $X_c^{ij}$ introduces a particle-related length scale on the distribution near the centreline, whereas (2.37) describes a distribution without a length scale.
$X_c^{ij}$ introduces a particle-related length scale on the distribution near the centreline, whereas (2.37) describes a distribution without a length scale.
Rivera et al. (Reference Rivera, Zhang and Graham2016) accommodated the non-vanishing diffusivities at the centreline but ignored variations in the drift velocity. This led to the prediction of a linear cusp at the centreline, as seen by inserting (41) from their paper into (2.10) to obtain
which yields ![]() $n\approx n_0(1-M_3 \lvert \tilde y\rvert )$, consistent with the result shown in figure 10 of their paper. Here,
$n\approx n_0(1-M_3 \lvert \tilde y\rvert )$, consistent with the result shown in figure 10 of their paper. Here, ![]() $M_3$ is a positive constant, and
$M_3$ is a positive constant, and ![]() $\tilde y=X_2/H$.
$\tilde y=X_2/H$.
The diffusive flux model (Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992) also predicts a linear cusp at the centreline, except with ![]() $n_0=n_{m}$, corresponding the maximum packing fraction, as shown in Appendix B. Although the diffusive flux model uses local coefficients for diffusivity and drift velocity in the particle transport equation (B1), the singular behaviour (2.37) is avoided through the use of a suspension viscosity model that diverges at a prescribed maximum packing fraction.
$n_0=n_{m}$, corresponding the maximum packing fraction, as shown in Appendix B. Although the diffusive flux model uses local coefficients for diffusivity and drift velocity in the particle transport equation (B1), the singular behaviour (2.37) is avoided through the use of a suspension viscosity model that diverges at a prescribed maximum packing fraction.
3. Stationary particle distributions: general results
The results presented in this section are independent of the character of pairwise particle interactions. Specific results for particles that undergo short-range contact interactions are presented in § 5.
3.1. Non-vanishing shear rates
Here, we present an exact stationary solution for the particle distribution in a polydisperse suspension in a flow with a power-law shear-rate magnitude,
where ![]() $\beta$ and
$\beta$ and ![]() $C_1$ are arbitrary non-zero constants and
$C_1$ are arbitrary non-zero constants and ![]() $X_2>0$ is assumed. Accordingly, the shear rate is non-vanishing (and non-singular).
$X_2>0$ is assumed. Accordingly, the shear rate is non-vanishing (and non-singular).
Inserting (2.19)–(2.24) into (2.10) yields
 \begin{equation} \sum_{j=1}^m (\dot{\gamma}[I_{ij2}^A\, n_{j} n_{i}' + (I_{ij2}^A+I_{ij2}^B)n_{i} n_{j}' ]+\dot{\gamma}'[n_{i}n_{j}(I_{ij2}^A+\tfrac{1}{2}I_{ij2}^B)])=0, \end{equation}
\begin{equation} \sum_{j=1}^m (\dot{\gamma}[I_{ij2}^A\, n_{j} n_{i}' + (I_{ij2}^A+I_{ij2}^B)n_{i} n_{j}' ]+\dot{\gamma}'[n_{i}n_{j}(I_{ij2}^A+\tfrac{1}{2}I_{ij2}^B)])=0, \end{equation}
for ![]() $i=1,2,\ldots, m$, where primes are used to denote
$i=1,2,\ldots, m$, where primes are used to denote ![]() $X_2$-derivatives.
$X_2$-derivatives.
A power-law particle distribution
is seen to satisfy (3.2) with arbitrary coefficients ![]() $c_i$. This is a general result that holds independent of the details of pairwise particle interactions in a given system. There are two features that should be noted here: (i) the effect of particle interactions exactly cancel, i.e. the spatial distribution of each particle species is unaffected by the presence of the others, and (ii) particle size does not affect the particle distribution. These features break down in regions where the shear rate vanishes, as seen below.
$c_i$. This is a general result that holds independent of the details of pairwise particle interactions in a given system. There are two features that should be noted here: (i) the effect of particle interactions exactly cancel, i.e. the spatial distribution of each particle species is unaffected by the presence of the others, and (ii) particle size does not affect the particle distribution. These features break down in regions where the shear rate vanishes, as seen below.
3.2. Planar Poiseuille flow
Here, we consider the steady-state particle distribution in quadratic flows (2.30), including regions ![]() $X_2\to 0$, where the shear rate vanishes.
$X_2\to 0$, where the shear rate vanishes.
3.2.1. Polydisperse suspension
Inserting (2.38)–(2.43) into (2.10) yields the equation governing the stationary particle distribution
 \begin{equation} \sum_{j=1}^m (\lvert X_2\rvert [I_{ij}^{(1)}(X_2) n_{j} n_{i}' + I_{ij}^{(2)}(X_2) n_{i} n_{j}' ]+I_{ij}^{(3)}(X_2) n_{i}n_{j})=0, \quad\vert X_2\vert < X_c, \end{equation}
\begin{equation} \sum_{j=1}^m (\lvert X_2\rvert [I_{ij}^{(1)}(X_2) n_{j} n_{i}' + I_{ij}^{(2)}(X_2) n_{i} n_{j}' ]+I_{ij}^{(3)}(X_2) n_{i}n_{j})=0, \quad\vert X_2\vert < X_c, \end{equation}
for ![]() $i=1,2,\ldots, m$. In a polydisperse system, each binary interaction has a distinct boundary-layer half-thickness,
$i=1,2,\ldots, m$. In a polydisperse system, each binary interaction has a distinct boundary-layer half-thickness, ![]() $X_c^{ij}$, determined by (2.36), and
$X_c^{ij}$, determined by (2.36), and ![]() $X_c$ is the maximum of these, i.e.
$X_c$ is the maximum of these, i.e.
For ![]() $\lvert X_2\rvert > X_c$, (3.4) reduces to (3.2), according to (2.51a–c), thus particle distributions are decoupled and obey distribution (3.3) with
$\lvert X_2\rvert > X_c$, (3.4) reduces to (3.2), according to (2.51a–c), thus particle distributions are decoupled and obey distribution (3.3) with ![]() $\beta =1$, i.e.
$\beta =1$, i.e.
where ![]() $n_{i c}$ is the number density of species
$n_{i c}$ is the number density of species ![]() $i$ at
$i$ at ![]() $X_2=X_c$.
$X_2=X_c$.
The spatial distributions of particle species are coupled for ![]() $\lvert X_2\rvert < X_c$. By contrast to the scale-free power-law distribution (3.3) that governs particle distributions in regions of non-vanishing shear rate, the coupling that occurs in regions of vanishing shear rate imposes a particle-related length scale
$\lvert X_2\rvert < X_c$. By contrast to the scale-free power-law distribution (3.3) that governs particle distributions in regions of non-vanishing shear rate, the coupling that occurs in regions of vanishing shear rate imposes a particle-related length scale ![]() $X_c$. A dimensionless coordinate is thus introduced using the length scale
$X_c$. A dimensionless coordinate is thus introduced using the length scale ![]() $X_c$
$X_c$
It will also be useful to define the dimensionless number densities
where ![]() $n_{i c}$ is the number density of particle species
$n_{i c}$ is the number density of particle species ![]() $i$ at
$i$ at ![]() $X_2=X_c$ and
$X_2=X_c$ and ![]() $n_c=\sum _{i=1}^m n_{i c}$.
$n_c=\sum _{i=1}^m n_{i c}$.
In terms of these variables, (3.4) becomes
 \begin{equation} \sum_{j=1}^m ( {D}_{ij}^{(1)}(y) \bar n_{j} \bar n_{i}' + {D}_{ij}^{(2)}(y) \bar n_{i} \bar n_{j}' +{V}_{ij}(y)\, \bar n_{i}\bar n_{j})=0, \quad \vert y\vert < 1, \end{equation}
\begin{equation} \sum_{j=1}^m ( {D}_{ij}^{(1)}(y) \bar n_{j} \bar n_{i}' + {D}_{ij}^{(2)}(y) \bar n_{i} \bar n_{j}' +{V}_{ij}(y)\, \bar n_{i}\bar n_{j})=0, \quad \vert y\vert < 1, \end{equation}
where primes denote ![]() $y$-derivatives and dimensionless transport coefficients are defined
$y$-derivatives and dimensionless transport coefficients are defined
Boundary conditions for (3.9) are given by
where ![]() $x_{i c}=n_{i c}/n_c$ is the number density fraction at
$x_{i c}=n_{i c}/n_c$ is the number density fraction at ![]() $y=1$. Outside of the coupled boundary-layer region,
$y=1$. Outside of the coupled boundary-layer region, ![]() $\lvert y\rvert > 1$, the dimensionless particle densities are given by
$\lvert y\rvert > 1$, the dimensionless particle densities are given by
according to (3.6).
The number densities ![]() $n_{ic}$ at
$n_{ic}$ at ![]() $y=1$ are related to the prescribed bulk number densities
$y=1$ are related to the prescribed bulk number densities ![]() $n_{i \infty }$, through the conservation constraint (2.11), which in this case becomes
$n_{i \infty }$, through the conservation constraint (2.11), which in this case becomes
for ![]() $i=1,\ldots, m$, where
$i=1,\ldots, m$, where ![]() ${v}(x)$ is the velocity (2.32),
${v}(x)$ is the velocity (2.32), ![]() $q=\frac {2}{3} {v}_0 H$ is the corresponding volume flux per unit depth and
$q=\frac {2}{3} {v}_0 H$ is the corresponding volume flux per unit depth and ![]() $H$ is the half-width of the channel. Using dimensionless variables and (3.12) yields
$H$ is the half-width of the channel. Using dimensionless variables and (3.12) yields
where ![]() $\bar n_{i \infty }=n_{i \infty }/n_{c}$ and
$\bar n_{i \infty }=n_{i \infty }/n_{c}$ and
is the ratio of the two length scales that affect the particle distributions. Under the assumption that the channel width is large compared with the particle size, ![]() $\epsilon \ll 1$. The quantity
$\epsilon \ll 1$. The quantity ![]() ${\rm \Delta} \bar N_i$ is the (average) deficit of type-
${\rm \Delta} \bar N_i$ is the (average) deficit of type-![]() $i$ particle density in the centre region compared with the singular distribution (3.12)
$i$ particle density in the centre region compared with the singular distribution (3.12)
where ![]() $\bar N_i$ is defined above. This particle deficit results from the modified transport coefficients in the region
$\bar N_i$ is defined above. This particle deficit results from the modified transport coefficients in the region ![]() $\vert y\vert < 1$. The
$\vert y\vert < 1$. The ![]() $O(\epsilon ^{5/2})$ error in (3.14) results from neglecting particle–wall interactions. Dividing (3.14) by its sum over all species provides a relation between the composition at
$O(\epsilon ^{5/2})$ error in (3.14) results from neglecting particle–wall interactions. Dividing (3.14) by its sum over all species provides a relation between the composition at ![]() $X_2=X_c$ and the bulk composition
$X_2=X_c$ and the bulk composition
 \begin{equation} x_{i \infty}=x_{i c}\left( \frac{ 1-\dfrac{5}{8}\epsilon^{1/2} {\rm \Delta} \bar N_i}{\displaystyle 1-\frac{5}{8}\epsilon^{1/2} \sum_{j=1}^m x_{j c}{\rm \Delta} \bar N_j}\right) +O(\epsilon^{2}), \end{equation}
\begin{equation} x_{i \infty}=x_{i c}\left( \frac{ 1-\dfrac{5}{8}\epsilon^{1/2} {\rm \Delta} \bar N_i}{\displaystyle 1-\frac{5}{8}\epsilon^{1/2} \sum_{j=1}^m x_{j c}{\rm \Delta} \bar N_j}\right) +O(\epsilon^{2}), \end{equation}
for ![]() $i=1,\ldots, m-1$, where
$i=1,\ldots, m-1$, where ![]() $x_{i \infty }=n_{i\infty }/n_\infty$ is the prescribed bulk number fraction of species
$x_{i \infty }=n_{i\infty }/n_\infty$ is the prescribed bulk number fraction of species ![]() $i$. This result in combination with (3.11) provides the boundary conditions for (3.4). In wide channels,
$i$. This result in combination with (3.11) provides the boundary conditions for (3.4). In wide channels, ![]() $\epsilon \ll 1$, the composition in the centre region is insensitive to channel width; at leading order, (3.17) yields
$\epsilon \ll 1$, the composition in the centre region is insensitive to channel width; at leading order, (3.17) yields ![]() $x_{i c}\approx x_{i \infty }$ and boundary conditions for (3.4) simplify to
$x_{i c}\approx x_{i \infty }$ and boundary conditions for (3.4) simplify to
Dividing ![]() $\bar n_i(y)$ by (3.14) yields the particle distributions normalized by their bulk number densities,
$\bar n_i(y)$ by (3.14) yields the particle distributions normalized by their bulk number densities,
where
 \begin{equation} f_i(\epsilon)=\frac{\frac{5}{12} \epsilon^{{-}1/2}}{1-\frac{5}{8} \epsilon^{1/2} {\rm \Delta} \bar N_i}. \end{equation}
\begin{equation} f_i(\epsilon)=\frac{\frac{5}{12} \epsilon^{{-}1/2}}{1-\frac{5}{8} \epsilon^{1/2} {\rm \Delta} \bar N_i}. \end{equation}Outside the centre region, this distribution reduces to
according to (3.12), where ![]() $\tilde y=X_2/H$. The result indicates that the channel width sets the length scale of the distribution for
$\tilde y=X_2/H$. The result indicates that the channel width sets the length scale of the distribution for ![]() $\vert y\vert > 1$.
$\vert y\vert > 1$.
3.2.2. Monodisperse particle distribution
For a single particle species, (3.9)–(3.11) reduce to the linear boundary value problem
where ![]() $\bar N$ is defined by (3.8b) and the index
$\bar N$ is defined by (3.8b) and the index ![]() $i$ is dropped to distinguish the monodisperse case. The transport coefficients are given by
$i$ is dropped to distinguish the monodisperse case. The transport coefficients are given by
The solution of boundary value problem (3.22) is
 \begin{equation} \bar N(y)=\exp\left( \int_{\vert y\vert }^{1} \frac{{V}(t)}{{D}(t)} \, {\rm d} t\right). \end{equation}
\begin{equation} \bar N(y)=\exp\left( \int_{\vert y\vert }^{1} \frac{{V}(t)}{{D}(t)} \, {\rm d} t\right). \end{equation}
For ![]() $\lvert y\rvert > 1$, the transport coefficients (3.23a,b) reduce to their local forms
$\lvert y\rvert > 1$, the transport coefficients (3.23a,b) reduce to their local forms
and thus ![]() ${V}(y)/{D}(y)=1/2y$, according to (2.51a–c), so that the outer solution (3.12) is recovered. Given that
${V}(y)/{D}(y)=1/2y$, according to (2.51a–c), so that the outer solution (3.12) is recovered. Given that ![]() ${D}(y)$ is non-vanishing and
${D}(y)$ is non-vanishing and ![]() ${V}(y)$ vanishes linearly for
${V}(y)$ vanishes linearly for ![]() $\lvert y\rvert \to 0$, as discussed in § 2.3.3, it follows that
$\lvert y\rvert \to 0$, as discussed in § 2.3.3, it follows that ![]() $\bar N$ has a maximum with
$\bar N$ has a maximum with ![]() ${\rm d}\bar N/{{\rm d} y}=0$ at
${\rm d}\bar N/{{\rm d} y}=0$ at ![]() $y=0$, consistent with the scaling predicted by (2.55). From the continuity of
$y=0$, consistent with the scaling predicted by (2.55). From the continuity of ![]() ${D}(y)$ and
${D}(y)$ and ![]() ${V}(y)$ up to their second derivatives at
${V}(y)$ up to their second derivatives at ![]() $\lvert y\rvert =1$, it follows that
$\lvert y\rvert =1$, it follows that ![]() $\bar N(y)$ is continuous up to its third derivative.
$\bar N(y)$ is continuous up to its third derivative.
From (3.19), we have
where ![]() $\bar N(y)$ is given by (3.24),
$\bar N(y)$ is given by (3.24), ![]() ${\rm \Delta} \bar N$ given by
${\rm \Delta} \bar N$ given by
 \begin{equation} {\rm \Delta} \bar N=\int_0^1 \left[ y^{{-}1/2}-\exp\left( \int_{\vert y\vert }^{1} \frac{{V}(t)}{{D}(t)} \, {\rm d} t\right) \right]\, {{\rm d} y}, \end{equation}
\begin{equation} {\rm \Delta} \bar N=\int_0^1 \left[ y^{{-}1/2}-\exp\left( \int_{\vert y\vert }^{1} \frac{{V}(t)}{{D}(t)} \, {\rm d} t\right) \right]\, {{\rm d} y}, \end{equation}and
 \begin{equation} f(\epsilon)=\frac{\frac{5}{12} \epsilon^{{-}1/2}}{1-\frac{5}{8} \epsilon^{1/2} {\rm \Delta}\bar N}. \end{equation}
\begin{equation} f(\epsilon)=\frac{\frac{5}{12} \epsilon^{{-}1/2}}{1-\frac{5}{8} \epsilon^{1/2} {\rm \Delta}\bar N}. \end{equation}3.2.3. Superposition approximation
The particle distribution in a polydisperse mixture with weak interactions between particles of different sizes can be approximated by a superposition of monodisperse distributions for each particle size (or size class).
Displacements resulting from collisions between particles of different sizes are usually smaller than displacements resulting from collisions between equal-size particles. This is true for particles that undergo contact interactions, as discussed in § 4.2, because collision rates diminish rapidly with size ratio (Adler Reference Adler1981; Wang, Zinchenko & Davis Reference Wang, Zinchenko and Davis1994; Reboucas & Loewenberg Reference Reboucas and Loewenberg2021b). Thus, the superposition approximation may be expected to hold for particles with vastly different sizes. It may be also expected to hold for similar-size particles because the effect is similar to increasing the total number density and the latter scales out of the equations, as explained in § 2.2.1. The superposition approximation is further supported by the fact that particle distributions are coupled only in the boundary layer; outside the boundary-layer particle distributions are decoupled, as shown in § 3.1.
According to the superposition approximation, distribution (3.19) reduces to
for ![]() $i=1,\ldots, m$. Here,
$i=1,\ldots, m$. Here,
where ![]() $\bar N(y_i)$,
$\bar N(y_i)$, ![]() ${\rm \Delta} \bar N$ and
${\rm \Delta} \bar N$ and ![]() $f(x)$ are given by (3.24) and (3.27) and (3.28);
$f(x)$ are given by (3.24) and (3.27) and (3.28); ![]() $X_c^{ii}$ is the boundary-layer thickness for a suspension of type-
$X_c^{ii}$ is the boundary-layer thickness for a suspension of type-![]() $i$ particles. The result reduces to the monodisperse distribution (3.26) by dropping the index
$i$ particles. The result reduces to the monodisperse distribution (3.26) by dropping the index ![]() $i$.
$i$.
Comparing (3.19) and (3.29) indicates that the superposition approximation is equivalent to ![]() $\epsilon ^{-1/2}\bar N_i(y_i)\simeq \epsilon _i^{-1/2}\bar N(y_i)$ and
$\epsilon ^{-1/2}\bar N_i(y_i)\simeq \epsilon _i^{-1/2}\bar N(y_i)$ and ![]() $\epsilon ^{1/2}{\rm \Delta} \bar N_i\simeq \epsilon _i^{1/2}{\rm \Delta} \bar N$ and, thus,
$\epsilon ^{1/2}{\rm \Delta} \bar N_i\simeq \epsilon _i^{1/2}{\rm \Delta} \bar N$ and, thus,
where ![]() $\chi _i$ is the ratio
$\chi _i$ is the ratio
and ![]() $\chi _i \leq 1$, according to (3.5).
$\chi _i \leq 1$, according to (3.5).
Under the assumption that ![]() $X_c^{ii}$ scales with particle size, the above results predict that particle segregation occurs in the boundary layer region with relative enrichment of smaller particles. The dependence of the centreline particle density on particle size is described by the function
$X_c^{ii}$ scales with particle size, the above results predict that particle segregation occurs in the boundary layer region with relative enrichment of smaller particles. The dependence of the centreline particle density on particle size is described by the function ![]() $f(\epsilon _i)$. According to (3.28), particle densities at the centreline scale approximately with the inverse square root of particle size, assuming that particles are small compared with channel width,
$f(\epsilon _i)$. According to (3.28), particle densities at the centreline scale approximately with the inverse square root of particle size, assuming that particles are small compared with channel width, ![]() $\epsilon _i\ll 1$. Distributions of smaller particles adhere more closely to the singular outer distribution (3.12) as reflected by their smaller average density deficit (3.16), according to (3.31b).
$\epsilon _i\ll 1$. Distributions of smaller particles adhere more closely to the singular outer distribution (3.12) as reflected by their smaller average density deficit (3.16), according to (3.31b).
The error of the superposition approximation, resulting from interactions between particles of different sizes in the boundary layer, is characterized by the polydisperse enrichment
where ![]() $\bar N_i(y)$ is the exact distribution for type-
$\bar N_i(y)$ is the exact distribution for type-![]() $i$ particles in a polydisperse suspension and
$i$ particles in a polydisperse suspension and ![]() $\chi _i^{-1/2}\bar N(y_i)$ is superposition approximation (3.31a). According to (3.16) and (3.31b), we have the relation
$\chi _i^{-1/2}\bar N(y_i)$ is superposition approximation (3.31a). According to (3.16) and (3.31b), we have the relation ![]() ${\rm \Delta} \bar N_i=\chi ^{1/2}{\rm \Delta} \bar N-{\rm \Delta} \bar N_{ij}$.
${\rm \Delta} \bar N_i=\chi ^{1/2}{\rm \Delta} \bar N-{\rm \Delta} \bar N_{ij}$.
4. Particle displacements
4.1. Contact interactions
Spherical particles that undergo short-range symmetry-breaking ‘contact’ interactions in shear flow are considered here, specifically, particles with surface roughness, permeable particles and emulsion drops. Pair trajectories of such particles are analytically integrated to yield formulas for binary cross-stream particle displacements ![]() ${\rm \Delta} X^{12}_k$,
${\rm \Delta} X^{12}_k$, ![]() ${\rm \Delta} X^{21}_k$ (
${\rm \Delta} X^{21}_k$ (![]() $k=2,3$) involving integrals of the standard pair mobility functions for spherical particles. Note that superscripts 1 and 2 are used in this section to refer to particle labels, not particle species, by contrast to the superscripts
$k=2,3$) involving integrals of the standard pair mobility functions for spherical particles. Note that superscripts 1 and 2 are used in this section to refer to particle labels, not particle species, by contrast to the superscripts ![]() $i$ and
$i$ and ![]() $j$ introduced earlier. Accordingly,
$j$ introduced earlier. Accordingly, ![]() ${\rm \Delta} X^{12}_k$ refers to the net displacement of particle-
${\rm \Delta} X^{12}_k$ refers to the net displacement of particle-![]() $1$ resulting from its collision with particle-
$1$ resulting from its collision with particle-![]() $2$ and vice versa for
$2$ and vice versa for ![]() ${\rm \Delta} X^{21}_k$, whereas
${\rm \Delta} X^{21}_k$, whereas ![]() ${\rm \Delta} X^{ij}_k$ is the net displacement of any type-
${\rm \Delta} X^{ij}_k$ is the net displacement of any type-![]() $i$ particle resulting from its collision with any type-
$i$ particle resulting from its collision with any type-![]() $j$ particle. Similarly, we will use
$j$ particle. Similarly, we will use ![]() $r_c$ to denote the collision cross-section for particles 1 and 2, by contrast with the quantity
$r_c$ to denote the collision cross-section for particles 1 and 2, by contrast with the quantity ![]() $r_c^{ij}$, defined by (2.27a,b), that refers to the collision cross-section for any type-
$r_c^{ij}$, defined by (2.27a,b), that refers to the collision cross-section for any type-![]() $i$ and
$i$ and ![]() $j$ particles. The particles have radii
$j$ particles. The particles have radii ![]() $a_1$ and
$a_1$ and ![]() $a_2$, and size ratio
$a_2$, and size ratio ![]() $\kappa =a_2/a_1$. We assign label 1 to the larger particle thus, only
$\kappa =a_2/a_1$. We assign label 1 to the larger particle thus, only ![]() $\kappa \leq 1$ needs consideration.
$\kappa \leq 1$ needs consideration.
Recall that the particles are assumed to be non-Brownian and neutrally buoyant. Here, creeping flow conditions are assumed, and particle inertia is neglected
4.1.1. Rough particles
According to the usual model for rough particles, surface asperities with size ![]() $d$ transmit a normal inter-particle contact force between rigid particles that prevents surface-to-surface particle separations less than
$d$ transmit a normal inter-particle contact force between rigid particles that prevents surface-to-surface particle separations less than ![]() $d$ but do not exert a tensile force upon separation. Here,
$d$ but do not exert a tensile force upon separation. Here, ![]() $\bar \delta = d/\bar a$ is the dimensionless roughness amplitude,
$\bar \delta = d/\bar a$ is the dimensionless roughness amplitude, ![]() $\bar a=(a_1+a_2)/2$ is the average particle radius and
$\bar a=(a_1+a_2)/2$ is the average particle radius and ![]() $\bar \delta \ll 1$ is assumed. Models for rough particles may also include a coefficient of friction to describe tangential forces transmitted by surface asperities at contact,
$\bar \delta \ll 1$ is assumed. Models for rough particles may also include a coefficient of friction to describe tangential forces transmitted by surface asperities at contact, ![]() $h_0=d$; the limiting cases of frictionless or tangentially locking particle contacts are most often used (Smart et al. Reference Smart, Beimfohr and Leighton1993; da Cunha & Hinch Reference da Cunha and Hinch1996; Rampall et al. Reference Rampall, Smart and Leighton1997; Wilson Reference Wilson2005).
$h_0=d$; the limiting cases of frictionless or tangentially locking particle contacts are most often used (Smart et al. Reference Smart, Beimfohr and Leighton1993; da Cunha & Hinch Reference da Cunha and Hinch1996; Rampall et al. Reference Rampall, Smart and Leighton1997; Wilson Reference Wilson2005).
4.1.2. Permeable particles
Particle permeability is another short-range, symmetry-breaking mechanism. The dimensionless permeability is defined ![]() $\bar K= k/\bar a^2$, where
$\bar K= k/\bar a^2$, where ![]() $k$ is the permeability and Darcy's law is used to describe the intraparticle flow. Weak permeability alleviates the lubrication pressure between particles, allowing particle contact,
$k$ is the permeability and Darcy's law is used to describe the intraparticle flow. Weak permeability alleviates the lubrication pressure between particles, allowing particle contact, ![]() $h_0=0$, but otherwise has little effect on the pair interaction. Under the assumption that the particles are rigid and not cohesive, the effect of weak permeability closely resembles small-amplitude particle roughness. The following hydrodynamic equivalence between particle roughness and particle permeability was proposed based on the contact time between particles under the action of a constant force (Reboucas & Loewenberg Reference Reboucas and Loewenberg2021a):
$h_0=0$, but otherwise has little effect on the pair interaction. Under the assumption that the particles are rigid and not cohesive, the effect of weak permeability closely resembles small-amplitude particle roughness. The following hydrodynamic equivalence between particle roughness and particle permeability was proposed based on the contact time between particles under the action of a constant force (Reboucas & Loewenberg Reference Reboucas and Loewenberg2021a):
where ![]() $\bar \delta$ and
$\bar \delta$ and ![]() $\bar K$ are the dimensionless particle roughness and permeability, and
$\bar K$ are the dimensionless particle roughness and permeability, and ![]() $\nu =2\kappa / (1+\kappa )^2$. This relation is based on the assumption that no-slip boundary conditions apply on the particle surfaces. This correlation has been shown to hold accurately for colliding pair trajectories in several types of flow (including shear) for a wide range of size ratios and permeabilities (Reboucas & Loewenberg Reference Reboucas and Loewenberg2021b).
$\nu =2\kappa / (1+\kappa )^2$. This relation is based on the assumption that no-slip boundary conditions apply on the particle surfaces. This correlation has been shown to hold accurately for colliding pair trajectories in several types of flow (including shear) for a wide range of size ratios and permeabilities (Reboucas & Loewenberg Reference Reboucas and Loewenberg2021b).
4.1.3. Non-coalescing spherical drops
The small, flattened thin film that forms in the near-contact region between approximately spherical emulsion drops in apparent contact, ![]() $h_0\approx 0$, under small-deformation conditions is a third short-range mechanism that breaks the symmetry of pair trajectories. Drop deformation is principally controlled by the capillary number,
$h_0\approx 0$, under small-deformation conditions is a third short-range mechanism that breaks the symmetry of pair trajectories. Drop deformation is principally controlled by the capillary number, ![]() $Ca=\mu \dot \gamma a/\sigma$, where
$Ca=\mu \dot \gamma a/\sigma$, where ![]() $\mu$ is the viscosity of the continuous-phase fluid,
$\mu$ is the viscosity of the continuous-phase fluid, ![]() $\dot \gamma$ is the magnitude of the local shear rate,
$\dot \gamma$ is the magnitude of the local shear rate, ![]() $a$ is the drop radius and
$a$ is the drop radius and ![]() $\sigma$ is surface tension; small-deformation conditions are characterized by
$\sigma$ is surface tension; small-deformation conditions are characterized by ![]() $Ca\ll 1$.
$Ca\ll 1$.
In the absence of van der Waals attraction, slow drainage from the film (Nemer et al. Reference Nemer, Chen, Papadopoulos, Blawzdziewicz and Loewenberg2004; Zinchenko & Davis Reference Zinchenko and Davis2005; Nemer et al. Reference Nemer, Chen, Papadopoulos, Bławzdziewicz and Loewenberg2007; Santoro & Loewenberg Reference Santoro and Loewenberg2009; Nemer et al. Reference Nemer, Santoro, Chen, Blawzdziewicz and Loewenberg2013) prevents drop coalescence in the compressional quadrant of the flow that would otherwise result between spherical drops (i.e. infinite surface tension) with tangentially mobile interfaces (Zinchenko Reference Zinchenko1978; Wang et al. Reference Wang, Zinchenko and Davis1994). The film quickly reverts as the drops rotate into the extensional quadrant of the flow and has little effect on their separation (Zinchenko Reference Zinchenko1984; Loewenberg & Hinch Reference Loewenberg and Hinch1997).
The foregoing discussion indicates that ![]() $Ca\to 0$ is a singular limit: spherical drops, characterized by
$Ca\to 0$ is a singular limit: spherical drops, characterized by ![]() $Ca=0$, undergo coalescence in shear flow for trajectories with sufficiently small offsets, but coalescence does not occur for
$Ca=0$, undergo coalescence in shear flow for trajectories with sufficiently small offsets, but coalescence does not occur for ![]() $Ca>0$. Non-coalescing spherical drops is a rigorous description for the pair interactions of drops in the small-deformation limit,
$Ca>0$. Non-coalescing spherical drops is a rigorous description for the pair interactions of drops in the small-deformation limit, ![]() $Ca\to 0$, and absence of van der Waals attraction. Hydrodynamic interactions are described by the mobility functions for spherical drops (Zinchenko Reference Zinchenko1978), augmented by an inter-particle force at contact,
$Ca\to 0$, and absence of van der Waals attraction. Hydrodynamic interactions are described by the mobility functions for spherical drops (Zinchenko Reference Zinchenko1978), augmented by an inter-particle force at contact, ![]() $h_0=0$, that acts along the line of centres and only in compression, preventing overlap in the compressional quadrant of the flow, but otherwise having no effect. According to this description, hydrodynamic interactions depend on size ratio and the drop- to continuous-phase viscosity ratio,
$h_0=0$, that acts along the line of centres and only in compression, preventing overlap in the compressional quadrant of the flow, but otherwise having no effect. According to this description, hydrodynamic interactions depend on size ratio and the drop- to continuous-phase viscosity ratio, ![]() $\lambda$, but are independent of the capillary number.
$\lambda$, but are independent of the capillary number.
Non-coalescing spherical drops is a model for pair interactions of drops and other deformable particles under small-deformation conditions. Its predictions for drop displacements in shear flow are supported by the boundary integral simulations of Loewenberg & Hinch (Reference Loewenberg and Hinch1997) for drops under finite-capillary-number conditions, where drop displacements were shown to be a weak function of ![]() $Ca$ and the predictions of non-coalescing spherical drops were shown to be in approximate agreement with exact simulations even for moderate capillary numbers (Loewenberg & Hinch Reference Loewenberg and Hinch1997). Boundary integral simulations of capsules and red blood cells also show an insensitivity to deformation for moderate capillary numbers (Pranay et al. Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010; Kumar & Graham Reference Kumar and Graham2011; Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013; Qi & Shaqfeh Reference Qi and Shaqfeh2017), suggesting that a similar simplified model may provide a good approximation.
$Ca$ and the predictions of non-coalescing spherical drops were shown to be in approximate agreement with exact simulations even for moderate capillary numbers (Loewenberg & Hinch Reference Loewenberg and Hinch1997). Boundary integral simulations of capsules and red blood cells also show an insensitivity to deformation for moderate capillary numbers (Pranay et al. Reference Pranay, Anekal, Hernandez-Ortiz and Graham2010; Kumar & Graham Reference Kumar and Graham2011; Omori et al. Reference Omori, Ishikawa, Imai and Yamaguchi2013; Qi & Shaqfeh Reference Qi and Shaqfeh2017), suggesting that a similar simplified model may provide a good approximation.
4.2. Trajectories of particles with contact interactions
Relative particle trajectories emanate from ![]() $x_1\to -\infty$ for
$x_1\to -\infty$ for ![]() $x_2^{-\infty }>0$ and from
$x_2^{-\infty }>0$ and from ![]() $x_1\to +\infty$ for
$x_1\to +\infty$ for ![]() $x_2^{-\infty }<0$. Apart from the contact interactions, trajectories are accurately described using standard pair mobility functions for spherical particles (or drops) in shear flow (Batchelor & Green Reference Batchelor and Green1972a; Zinchenko Reference Zinchenko1978, Reference Zinchenko1980, Reference Zinchenko1983). Accordingly, particles with short-range binary contact interactions have circular upstream collision cross-sections, defined by (2.27a,b), where
$x_2^{-\infty }<0$. Apart from the contact interactions, trajectories are accurately described using standard pair mobility functions for spherical particles (or drops) in shear flow (Batchelor & Green Reference Batchelor and Green1972a; Zinchenko Reference Zinchenko1978, Reference Zinchenko1980, Reference Zinchenko1983). Accordingly, particles with short-range binary contact interactions have circular upstream collision cross-sections, defined by (2.27a,b), where ![]() $r_c$ depends on size ratio, and on the roughness, permeability, or drop- to continuous-phase viscosity ratio, respectively, for rough or permeable particles or drops. Collision cross-sections, or equivalently collision efficiencies
$r_c$ depends on size ratio, and on the roughness, permeability, or drop- to continuous-phase viscosity ratio, respectively, for rough or permeable particles or drops. Collision cross-sections, or equivalently collision efficiencies ![]() $E_{12}=(r_c/(2\bar a))^3$, are available in the literature for rough and permeable particles and drops (Wang et al. Reference Wang, Zinchenko and Davis1994; Reboucas & Loewenberg Reference Reboucas and Loewenberg2021b). Trajectories with offsets
$E_{12}=(r_c/(2\bar a))^3$, are available in the literature for rough and permeable particles and drops (Wang et al. Reference Wang, Zinchenko and Davis1994; Reboucas & Loewenberg Reference Reboucas and Loewenberg2021b). Trajectories with offsets ![]() $r^{-\infty } > r_c$ are reversible, i.e.
$r^{-\infty } > r_c$ are reversible, i.e. ![]() ${\rm \Delta} X_k^{12}={\rm \Delta} X_k^{21}=0$.
${\rm \Delta} X_k^{12}={\rm \Delta} X_k^{21}=0$.
Pair trajectories with upstream trajectory offsets, ![]() $r^{-\infty }< r_c$, reach the contact surface, defined by
$r^{-\infty }< r_c$, reach the contact surface, defined by ![]() $s=s^*$, where
$s=s^*$, where ![]() $s=r/\bar a$ is the centre-to-centre separation,
$s=r/\bar a$ is the centre-to-centre separation, ![]() $r$, normalized by the average particle radius. For permeable particles and drops,
$r$, normalized by the average particle radius. For permeable particles and drops, ![]() $s^*=2$; for particles with surface roughness,
$s^*=2$; for particles with surface roughness, ![]() $s=2+\bar \delta$. On the contact surface, the particles undergo relative rotation through the compressional quadrant of the flow and separate at the equator (
$s=2+\bar \delta$. On the contact surface, the particles undergo relative rotation through the compressional quadrant of the flow and separate at the equator (![]() $x_1=0$), under the assumption that cohesive forces are absent. The motion on the contact surface is described by a subset of the trajectory equations corresponding to zero relative radial velocity. Examples of contacting trajectories are shown in figures 4 and 5.
$x_1=0$), under the assumption that cohesive forces are absent. The motion on the contact surface is described by a subset of the trajectory equations corresponding to zero relative radial velocity. Examples of contacting trajectories are shown in figures 4 and 5.

Figure 4. Relative (a) and pair (b) particle trajectories in velocity-gradient plane, size ratio ![]() $\kappa =a_2/a_1=1/2$, roughness
$\kappa =a_2/a_1=1/2$, roughness ![]() $\bar \delta =d/\bar a=10^{-3}$; initial positions (i), contact surface (ii)–(iii) (dotted lines), final positions (iv). Relative
$\bar \delta =d/\bar a=10^{-3}$; initial positions (i), contact surface (ii)–(iii) (dotted lines), final positions (iv). Relative ![]() $\boldsymbol {x}=\boldsymbol {X}^{(2)}-\boldsymbol {X}^{(1)}$ and pair
$\boldsymbol {x}=\boldsymbol {X}^{(2)}-\boldsymbol {X}^{(1)}$ and pair ![]() $\bar {\boldsymbol {x}} =\boldsymbol {X}^{(1)}+\boldsymbol {X}^{(2)}$ coordinates of particles non-dimensionalized by the average radius
$\bar {\boldsymbol {x}} =\boldsymbol {X}^{(1)}+\boldsymbol {X}^{(2)}$ coordinates of particles non-dimensionalized by the average radius ![]() $\bar a=\frac {1}{2}(a_1+a_2)$; initial conditions
$\bar a=\frac {1}{2}(a_1+a_2)$; initial conditions ![]() $\boldsymbol {x}=(-\infty,0.1,0)$ and
$\boldsymbol {x}=(-\infty,0.1,0)$ and ![]() $\bar {\boldsymbol {x}}=(-\infty,0.1,0)$.
$\bar {\boldsymbol {x}}=(-\infty,0.1,0)$.

Figure 5. Offset relative trajectory shown in cross-flow plane (a) and enlargement (b), size ratio ![]() $\kappa =a_2/a_1=1/2$; particles with roughness
$\kappa =a_2/a_1=1/2$; particles with roughness ![]() $\bar \delta = d/\bar a= 5 \times 10^{-3}$, frictionless contact (solid lines), infinite contact friction coefficient (dash-dotted lines); permeable particles
$\bar \delta = d/\bar a= 5 \times 10^{-3}$, frictionless contact (solid lines), infinite contact friction coefficient (dash-dotted lines); permeable particles ![]() $\bar K=6\times 10^{-6}$ from (4.1) (dotted lines); drops with viscosity ratio
$\bar K=6\times 10^{-6}$ from (4.1) (dotted lines); drops with viscosity ratio ![]() $\lambda =1$ (dashed lines); initial offset (i), contact surface (ii)–(iii), final offset (iv); collision surface
$\lambda =1$ (dashed lines); initial offset (i), contact surface (ii)–(iii), final offset (iv); collision surface ![]() $s^*$ (large circle), collision cross-sections
$s^*$ (large circle), collision cross-sections ![]() $r_c$ particles (small circle), drops (dashed circle). Relative
$r_c$ particles (small circle), drops (dashed circle). Relative ![]() $\boldsymbol {x}=\boldsymbol {X}^{(2)}-\boldsymbol {X}^{(1)}$ coordinates of particles non-dimensionalized by the average radius
$\boldsymbol {x}=\boldsymbol {X}^{(2)}-\boldsymbol {X}^{(1)}$ coordinates of particles non-dimensionalized by the average radius ![]() $\bar a=\frac {1}{2}(a_1+a_2)$; initial conditions
$\bar a=\frac {1}{2}(a_1+a_2)$; initial conditions ![]() $\boldsymbol {x}=(-\infty,0.25,0.25)$.
$\boldsymbol {x}=(-\infty,0.25,0.25)$.
Below a critical roughness, the collision cross-section for rough particles vanishes; similarly, there exists a critical permeability below which ![]() $r_c=0$. The values of these critical parameters increase with diminishing size ratio (Arp & Mason Reference Arp and Mason1977; Reboucas & Loewenberg Reference Reboucas and Loewenberg2021b). Likewise, drops have a critical viscosity ratio beyond which
$r_c=0$. The values of these critical parameters increase with diminishing size ratio (Arp & Mason Reference Arp and Mason1977; Reboucas & Loewenberg Reference Reboucas and Loewenberg2021b). Likewise, drops have a critical viscosity ratio beyond which ![]() $r_c=0$, and the critical viscosity ratio decreases with diminishing size ratio (Wang et al. Reference Wang, Zinchenko and Davis1994). Equivalently, there exists a finite critical size ratio ratio,
$r_c=0$, and the critical viscosity ratio decreases with diminishing size ratio (Wang et al. Reference Wang, Zinchenko and Davis1994). Equivalently, there exists a finite critical size ratio ratio, ![]() $\kappa ^*$, below which
$\kappa ^*$, below which ![]() $r_c=0$ for fixed values of particle roughness or permeability, or drop viscosity ratio.
$r_c=0$ for fixed values of particle roughness or permeability, or drop viscosity ratio.
4.2.1. Maximum particle displacements
Maximum particle displacements are important because they determine the thickness of the boundary layer that forms in regions of vanishing shear rate. Maximum displacement magnitudes in the ![]() $X_2$-direction are achieved for
$X_2$-direction are achieved for ![]() $r^{-\infty }\to 0$ with
$r^{-\infty }\to 0$ with ![]() $\theta =\pm {\rm \pi}/2$ (i.e.
$\theta =\pm {\rm \pi}/2$ (i.e. ![]() $x_3^{-\infty }=0$). For contact interactions between pairs of inertialess particles in creeping flows, the maximum displacement magnitudes satisfy
$x_3^{-\infty }=0$). For contact interactions between pairs of inertialess particles in creeping flows, the maximum displacement magnitudes satisfy
and for equal-size particles,
by symmetry.
Bounds for the magnitudes of individual displacements of unequal size particles are given by
and for extreme size ratios,
4.3. Results
In Appendix C, particle trajectories, and net displacements, ![]() ${\rm \Delta} X_k^{12}$ and
${\rm \Delta} X_k^{12}$ and ![]() ${\rm \Delta} X_k^{21}$, are expressed in terms of formulas involving quadratures of pair mobility functions for spherical particles. Results for particle displacements are used to determine particle distributions in § 5. Examples of particle trajectories, and particle displacements are shown here and discussed.
${\rm \Delta} X_k^{21}$, are expressed in terms of formulas involving quadratures of pair mobility functions for spherical particles. Results for particle displacements are used to determine particle distributions in § 5. Examples of particle trajectories, and particle displacements are shown here and discussed.
4.3.1. Effects of friction and permeability
Contact friction can affect the relative motion of rough particles in contact. As explained in § C.4, it enhances particle displacements in the ![]() $X_2$-direction and suppresses them in the
$X_2$-direction and suppresses them in the ![]() $X_3$-direction. This behaviour is supported by computations of self- and gradient diffusivities (2.22) and (2.23) of equal-size particles by da Cunha & Hinch (Reference da Cunha and Hinch1996) for the limiting cases of frictionless and tangentially locking particle contacts, i.e. the latter produced larger diffusivities in the
$X_3$-direction. This behaviour is supported by computations of self- and gradient diffusivities (2.22) and (2.23) of equal-size particles by da Cunha & Hinch (Reference da Cunha and Hinch1996) for the limiting cases of frictionless and tangentially locking particle contacts, i.e. the latter produced larger diffusivities in the ![]() $X_2$-direction and smaller in the
$X_2$-direction and smaller in the ![]() $X_3$-direction. Similar results were obtained for the two limiting cases, however.
$X_3$-direction. Similar results were obtained for the two limiting cases, however.
An example of relative trajectories for the limiting cases of frictionless and tangentially locking particle contacts are contrasted in figure 5 (solid and dash-dotted lines) for size ratio ![]() $\kappa =1/2$. Very similar trajectories are obtained for the two cases but the enlargement shown in panel (b) of the figure concurs that friction enhances particle displacement in the
$\kappa =1/2$. Very similar trajectories are obtained for the two cases but the enlargement shown in panel (b) of the figure concurs that friction enhances particle displacement in the ![]() $X_2$-direction and suppresses it in the
$X_2$-direction and suppresses it in the ![]() $X_3$-direction. The insensitivity to contact friction seen here and in the results of da Cunha & Hinch (Reference da Cunha and Hinch1996) indicate that lubrication resistance dominates the effect of friction. Contact friction was neglected for all other rough particle calculations presented herein.
$X_3$-direction. The insensitivity to contact friction seen here and in the results of da Cunha & Hinch (Reference da Cunha and Hinch1996) indicate that lubrication resistance dominates the effect of friction. Contact friction was neglected for all other rough particle calculations presented herein.
The trajectory for permeable particles depicted by the dotted line in figure 5(b) lies between the two trajectories for rough particles, corresponding to the limiting cases of contact friction. This example illustrates a general result explained in § C.4.1. The displacements of permeable particles lie between the results for rough particles with frictionless and tangentially locking particle contacts and roughness prescribed by (4.1). These limits provide tight bounds on displacements of permeable particles inasmuch as rough particle displacements are insensitive to contact friction.
This finding and the reliability of correlation (4.1) on colliding trajectories that terminate on the contact surface discussed in § 4.1.2 supports its use for contacting trajectories in their entirety. It follows that pair displacements and thus transport of permeable particles can be reliably predicted from results for rough particles with either frictionless or tangentially locking particle contacts using (4.1).
4.3.2. Particle displacements
Examples of net particle displacements for unequal size rough particles and drops in the velocity-gradient and vorticity directions are shown by the contour maps in figures 6 and 7. Figures 8 and 9 show the collision cross-section (and maximum displacement) for equal-size particles as functions of particle roughness and drop viscosity. Figures 10 and 11 show maximum particle displacements as a function of size ratio, illustrating relations (4.2)–(4.5a–c).

Figure 6. Displacement magnitudes of (a) larger and (b) smaller particles in velocity-gradient direction, and (c) larger and (d) smaller particles in vorticity direction; size ratio ![]() $\kappa =a_2/a_1=1/2$, roughness
$\kappa =a_2/a_1=1/2$, roughness ![]() $\bar \delta =d/\bar a=10^{-3}$. Displacements and cross-flow coordinates non-dimensionalized by the average radius,
$\bar \delta =d/\bar a=10^{-3}$. Displacements and cross-flow coordinates non-dimensionalized by the average radius, ![]() $\bar a=\frac {1}{2}(a_1+a_2)$; radius of collision cross-section,
$\bar a=\frac {1}{2}(a_1+a_2)$; radius of collision cross-section, ![]() $r_c$, indicated by outermost quarter circle. By the symmetry relations (2.7) and (2.8a,b), only a quarter of the cross-flow plane is shown.
$r_c$, indicated by outermost quarter circle. By the symmetry relations (2.7) and (2.8a,b), only a quarter of the cross-flow plane is shown.

Figure 7. Same as figure 6, except for drops with viscosity ratio ![]() $\lambda =1$.
$\lambda =1$.

Figure 8. Collision cross-section for equal-size particles with roughness ![]() $\delta =d/a$ normalized by particle radius.
$\delta =d/a$ normalized by particle radius.

Figure 9. Same as figure 8, except for drops with viscosity ratio ![]() $\lambda$.
$\lambda$.

Figure 10. Maximum particle displacement magnitudes (solid lines) for rough particles, ![]() $\delta _1=d/a_1=10^{-3}$, vs size ratio,
$\delta _1=d/a_1=10^{-3}$, vs size ratio, ![]() $\kappa =a_2/a_1$, (a) in the velocity-gradient direction, and (b) in the vorticity direction; average of maximum displacement magnitudes (dashed lines); particle displacements and collision cross-section non-dimensionalized by radius of larger particle
$\kappa =a_2/a_1$, (a) in the velocity-gradient direction, and (b) in the vorticity direction; average of maximum displacement magnitudes (dashed lines); particle displacements and collision cross-section non-dimensionalized by radius of larger particle ![]() $a_1$.
$a_1$.

Figure 11. Same as figure 10, except for drops with viscosity ratio ![]() $\lambda =1$.
$\lambda =1$.
The results in figures 5–11 illustrate that (i) particle displacements in the velocity-gradient direction are considerably larger than in the vorticity direction, especially for rough particles, and (ii) pair collisions displace the smaller particle much more than the larger, even for modest size ratios (beyond the critical value).
4.4. Boundary-layer thickness
Given that maximum displacements (4.2) occur for ![]() $r^{-\infty }\to 0$ and given
$r^{-\infty }\to 0$ and given ![]() ${\rm \Delta} X^{12}_{2}={\rm \Delta} X^{21}_{2}=0$ for
${\rm \Delta} X^{12}_{2}={\rm \Delta} X^{21}_{2}=0$ for ![]() $r^{-\infty }=r_c$, suggests that (2.36) can be replaced by the tighter bound
$r^{-\infty }=r_c$, suggests that (2.36) can be replaced by the tighter bound
for particles of types ![]() $i$ and
$i$ and ![]() $j$ that undergo contact interactions. Our calculations support this relation but our results do not rely on it. The relation is used here to discuss the width of the boundary layer,
$j$ that undergo contact interactions. Our calculations support this relation but our results do not rely on it. The relation is used here to discuss the width of the boundary layer, ![]() $X_c$, that forms where the shear rate vanishes.
$X_c$, that forms where the shear rate vanishes.
In a monodisperse suspension, maximum particle displacements are set by the collision cross-section, according to (4.3a,b), and ![]() $r_c=r_c^{ii}$, thus the boundary-layer thickness (4.6) reduces to
$r_c=r_c^{ii}$, thus the boundary-layer thickness (4.6) reduces to
The formula for the collision cross-section is provided in Appendix C. Below the critical values of particle roughness or permeability or above a critical value of the drop viscosity ratio, ![]() $r_c=0$, as seen in figures 8 and 9; particle structuring is not predicted in this case.
$r_c=0$, as seen in figures 8 and 9; particle structuring is not predicted in this case.
In a bidisperse suspension we have,
given that ![]() ${\rm \Delta} X_2^{21}\geq {\rm \Delta} X_2^{12}$, according to (4.4a–c). Here,
${\rm \Delta} X_2^{21}\geq {\rm \Delta} X_2^{12}$, according to (4.4a–c). Here, ![]() $r_{c,{max}}$ is the maximum collision cross-section among the permutations of pairs of type-
$r_{c,{max}}$ is the maximum collision cross-section among the permutations of pairs of type-![]() $i$ and
$i$ and ![]() $j$ particles, i.e.
$j$ particles, i.e. ![]() $r_{c,{max}}=max (r_c^{ii}, r_c^{jj}, r_c^{ij})$. In binary mixtures of particles that differ only in size, the collision cross-section between the larger particles usually controls
$r_{c,{max}}=max (r_c^{ii}, r_c^{jj}, r_c^{ij})$. In binary mixtures of particles that differ only in size, the collision cross-section between the larger particles usually controls ![]() $r_{c,{max}}$. Consider the case where larger particles are type-
$r_{c,{max}}$. Consider the case where larger particles are type-![]() $i$ and smaller, type
$i$ and smaller, type ![]() $j$, particles differs only in size and
$j$, particles differs only in size and ![]() $\kappa < 1$. In this case, we have
$\kappa < 1$. In this case, we have ![]() $r_c^{ii}> r_c^{ij}$ because collision cross-sections increase monotonically with size ratio, and usually
$r_c^{ii}> r_c^{ij}$ because collision cross-sections increase monotonically with size ratio, and usually ![]() $r_c^{ii} > r_c^{jj}$, because collision cross-sections scale with particle size. Accordingly, we have
$r_c^{ii} > r_c^{jj}$, because collision cross-sections scale with particle size. Accordingly, we have ![]() $r_{c,{max}}=r_c^{ii}$. For drops,
$r_{c,{max}}=r_c^{ii}$. For drops, ![]() $r_c^{ii} =\kappa ^{-1} r_c^{jj}$ but this relation is inexact for rough and permeable particles because collision cross-sections increase monotonically with the size-dependent parameters,
$r_c^{ii} =\kappa ^{-1} r_c^{jj}$ but this relation is inexact for rough and permeable particles because collision cross-sections increase monotonically with the size-dependent parameters, ![]() $d/a$ and
$d/a$ and ![]() $k/a^2$. Away from critical values of these parameters, however, the dependence is sub-linear, as seen in figure 8, thus
$k/a^2$. Away from critical values of these parameters, however, the dependence is sub-linear, as seen in figure 8, thus ![]() $r_c^{ii} > r_c^{jj}$ holds and the relation
$r_c^{ii} > r_c^{jj}$ holds and the relation ![]() $r_{c,{max}}=r_c^{ii}$ is retained.
$r_{c,{max}}=r_c^{ii}$ is retained.
The results shown in figures 10 and 11 illustrate relation (4.8), indicating that the boundary-layer thickness is controlled by heterogeneous pair interactions (i.e. ![]() ${\rm \Delta} _{2, {max}}^{21} > r_{c,{max}}$) for moderate size ratios, and by the collision cross-section of the larger particles closer to the critical size ratio,
${\rm \Delta} _{2, {max}}^{21} > r_{c,{max}}$) for moderate size ratios, and by the collision cross-section of the larger particles closer to the critical size ratio, ![]() $\kappa ^*$. For
$\kappa ^*$. For ![]() $\kappa <\kappa ^*$, displacements due to interactions between particles of different sizes vanish identically; in this case, the superposition approximation, described in § 3.2.3, holds exactly.
$\kappa <\kappa ^*$, displacements due to interactions between particles of different sizes vanish identically; in this case, the superposition approximation, described in § 3.2.3, holds exactly.
For particles with contact interactions, pair displacements and the resulting boundary-layer thickness scale with the size of the suspended particles. The particle distributions described in § 3.2 thus depend on particle size.
5. Particle distributions in Poiseuille flow: particles with contact interactions
Stationary particle distributions are presented here for suspensions in planar Poiseuille flow (2.32) with particles that undergo contact interactions using the analysis developed in § 4. The results here are specific examples of the results presented in § 3 for the case of rough particles and emulsion drops; permeable particles are also included through the established relation (4.1). The predictions for rough particles are compared with experimental measurements. No adjustable parameters are used for this comparison, aside from particle roughness; a nominal ![]() $1\,\%$ roughness is used in all cases.
$1\,\%$ roughness is used in all cases.
Transport coefficients (3.10a,b) were obtained by numerical evaluation of integrals (2.44)–(2.46) with particle displacements, ![]() ${\rm \Delta} X_2^{ij}$, obtained from quadratures of mobility functions, as described in § C.3. Stationary particle distributions in monodisperse suspensions were then obtained by evaluating formula (3.24). Stationary particle distributions in bidisperse mixtures were obtained by numerical integration of (3.9) using boundary conditions (3.18) appropriate for wide channels; approximate distributions were obtained by the superposition approximation (3.29). Results for monodisperse and bidisperse suspensions are presented in §§ 5.1 and 5.2, respectively. The limitation to dilute suspensions is discussed in § 5.3 and a practical upper bound on the volume fraction is proposed.
${\rm \Delta} X_2^{ij}$, obtained from quadratures of mobility functions, as described in § C.3. Stationary particle distributions in monodisperse suspensions were then obtained by evaluating formula (3.24). Stationary particle distributions in bidisperse mixtures were obtained by numerical integration of (3.9) using boundary conditions (3.18) appropriate for wide channels; approximate distributions were obtained by the superposition approximation (3.29). Results for monodisperse and bidisperse suspensions are presented in §§ 5.1 and 5.2, respectively. The limitation to dilute suspensions is discussed in § 5.3 and a practical upper bound on the volume fraction is proposed.
In addition to diluteness, experiments for comparison require small particle Reynolds numbers and large Péclet numbers,
where ![]() $\rho$ and
$\rho$ and ![]() $\mu$ are the density and viscosity of the suspending phase fluid,
$\mu$ are the density and viscosity of the suspending phase fluid, ![]() $\mathcal {D}$ is the Stokes–Einstein diffusivity,
$\mathcal {D}$ is the Stokes–Einstein diffusivity, ![]() $v_0$ is the magnitude of the centreline velocity and
$v_0$ is the magnitude of the centreline velocity and ![]() $H$ is the half-width of the channel. The Reynolds number is based on the characteristic shear rate,
$H$ is the half-width of the channel. The Reynolds number is based on the characteristic shear rate, ![]() $v_0/H$, and the Péclet number is defined by criterion (2.33). For all experimental comparisons in this paper,
$v_0/H$, and the Péclet number is defined by criterion (2.33). For all experimental comparisons in this paper, ![]() $Re < 10^{-3}$ and
$Re < 10^{-3}$ and ![]() $Pe > 10^7$. In bidisperse suspensions, these bounds apply with Reynolds number based on the larger particle and Péclet number based on the smaller. The assumptions of non-Brownian particles and creeping flow conditions are thus easily justified.
$Pe > 10^7$. In bidisperse suspensions, these bounds apply with Reynolds number based on the larger particle and Péclet number based on the smaller. The assumptions of non-Brownian particles and creeping flow conditions are thus easily justified.
Another important consideration is the entry length ![]() $L_{ss}$ required for particles to achieve a stationary distribution. An estimate for this quantity is given by
$L_{ss}$ required for particles to achieve a stationary distribution. An estimate for this quantity is given by ![]() $L_{ss}\sim v_0 t_{ss}$, where
$L_{ss}\sim v_0 t_{ss}$, where ![]() $t_{ss}$ is the corresponding time scale for cross-flow particle transport. The latter scales as
$t_{ss}$ is the corresponding time scale for cross-flow particle transport. The latter scales as ![]() $t_{ss}\sim H^2/{D}$, where
$t_{ss}\sim H^2/{D}$, where ![]() ${D}=O(\dot {\gamma } n_{\infty } X_c^5)$ is an estimate for the magnitude of the hydrodynamic diffusion coefficient of the particle. Then taking
${D}=O(\dot {\gamma } n_{\infty } X_c^5)$ is an estimate for the magnitude of the hydrodynamic diffusion coefficient of the particle. Then taking ![]() $\dot {\gamma }\sim v_0/H$ and
$\dot {\gamma }\sim v_0/H$ and ![]() $X_c=O(a)$, yields the desired estimate for the entry length based on the dilute theory
$X_c=O(a)$, yields the desired estimate for the entry length based on the dilute theory
 \begin{equation} \left(\frac{L}{H}\right)_{ss}= \frac{1}{12 \phi_{\infty}} \left(\frac{H}{a}\right)^2, \end{equation}
\begin{equation} \left(\frac{L}{H}\right)_{ss}= \frac{1}{12 \phi_{\infty}} \left(\frac{H}{a}\right)^2, \end{equation}
where the factor of 12 is included for consistency with Nott & Brady (Reference Nott and Brady1994). Accordingly, this estimate is the same as theirs except for the explicit first-order dependence on volume fraction. In a dilute polydisperse suspension, particles of different sizes ![]() $a_i$ may require different entry lengths
$a_i$ may require different entry lengths ![]() $L_i$ to establish a stationary distribution, consistent with the superposition approximation. Thus, we introduce the generalization
$L_i$ to establish a stationary distribution, consistent with the superposition approximation. Thus, we introduce the generalization
 \begin{equation} \left(\frac{L_i}{H}\right)_{ss}= \frac{1}{12 \phi_{i \infty}}\left(\frac{H}{a_i}\right)^2. \end{equation}
\begin{equation} \left(\frac{L_i}{H}\right)_{ss}= \frac{1}{12 \phi_{i \infty}}\left(\frac{H}{a_i}\right)^2. \end{equation}
Entry lengths ![]() $L_{exp}$ used in experiments to test the predicted stationary distributions must satisfy
$L_{exp}$ used in experiments to test the predicted stationary distributions must satisfy
where the index ![]() $i$ is omitted for monodisperse suspensions. This criterion is satisfied for most of the experimental comparisons presented below, but as noted below, there are exceptions. The value of
$i$ is omitted for monodisperse suspensions. This criterion is satisfied for most of the experimental comparisons presented below, but as noted below, there are exceptions. The value of ![]() $L_{exp}/L_{i_{ss}}$ is reported in the figure captions with experimental comparisons.
$L_{exp}/L_{i_{ss}}$ is reported in the figure captions with experimental comparisons.
Dimensionless variables are used in this section with characteristic length set by the boundary-layer thickness ![]() $X_c$, the boundary layer thicknesses of individual species
$X_c$, the boundary layer thicknesses of individual species ![]() $X_c^{ii}$ (related to the collision cross-section by (4.7)), or the channel width
$X_c^{ii}$ (related to the collision cross-section by (4.7)), or the channel width ![]() $H$, as indicated. The normalized number density
$H$, as indicated. The normalized number density ![]() $\bar N_i$, defined by (3.8b), is used for presenting theoretical predictions (i.e. the number density of each particle species normalized by its density at edge of the boundary layer).
$\bar N_i$, defined by (3.8b), is used for presenting theoretical predictions (i.e. the number density of each particle species normalized by its density at edge of the boundary layer).
5.1. Particle distribution in monodisperse suspensions
Results for monodisperse suspensions are presented here, including particle distributions, the average deficit of particle density in the boundary layer compared with the singular outer distribution and the underlying diffusive and drift velocity transport coefficients. Predicted particle distributions are compared with predictions of the diffusive flux model (Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992) and the experiments of Koh et al. (Reference Koh, Hookham and Leal1994).
The results in figure 12 show that the drift velocity ![]() ${V}$ but not the diffusion coefficient
${V}$ but not the diffusion coefficient ![]() ${D}$ vanishes at the centre of the channel, where the shear rate vanishes, and illustrate the respective odd and even symmetries of these quantities and their behaviour for
${D}$ vanishes at the centre of the channel, where the shear rate vanishes, and illustrate the respective odd and even symmetries of these quantities and their behaviour for ![]() $X_2\to 0$, as discussed in § 2.3.3. These are the essential features that avoid the classical singularity at points of vanishing shear rate predicted by (2.37) and instead yield the smooth, non-singular behaviour predicted by (2.55). The dashed lines in figure 12 depict the local form of the transport coefficients that apply for
$X_2\to 0$, as discussed in § 2.3.3. These are the essential features that avoid the classical singularity at points of vanishing shear rate predicted by (2.37) and instead yield the smooth, non-singular behaviour predicted by (2.55). The dashed lines in figure 12 depict the local form of the transport coefficients that apply for ![]() $X_2>X_c$. The anticipated second-derivative discontinuity in the transport coefficients at
$X_2>X_c$. The anticipated second-derivative discontinuity in the transport coefficients at ![]() $X_2=X_c$, discussed in § 2.3.3, is evident.
$X_2=X_c$, discussed in § 2.3.3, is evident.

Figure 12. Dimensionless drift velocity (a) and diffusive (b) transport coefficients ![]() $\bar {{D}}=D X_c^{-6}$ and
$\bar {{D}}=D X_c^{-6}$ and ![]() $\bar {{V}}=V X_c^{-5}$ (3.23a,b) for monodisperse suspensions of particles with roughness
$\bar {{V}}=V X_c^{-5}$ (3.23a,b) for monodisperse suspensions of particles with roughness ![]() $\delta =d/a$ and drops with viscosity ratio
$\delta =d/a$ and drops with viscosity ratio ![]() $\lambda$, as indicated (solid lines); outer forms of transport coefficients (3.25a,b) (dotted lines). Boundary-layer thicknesses
$\lambda$, as indicated (solid lines); outer forms of transport coefficients (3.25a,b) (dotted lines). Boundary-layer thicknesses ![]() $X_c/a=0.349$ for rough particles, and
$X_c/a=0.349$ for rough particles, and ![]() $X_c/a=0.778$ for drops.
$X_c/a=0.778$ for drops.
Examples of particle distributions for rough particles and emulsion drops are shown in figure 13; the two distributions are barely distinguishable. Similar results were obtained for other values of roughness and viscosity ratios. The average deficit of particle density in the boundary layer is insensitive to the particle parameters (roughness and viscosity ratio) and has an almost constant value, ![]() $0.711 \leq {\rm \Delta} \bar N\leq 0.714$, over a wide range of parameters, as seen in figure 14. The boundary-layer thickness (4.7) depends on details of the contact interactions between particles, as shown in figures 8 and 9; however, the particle distributions are almost independent of these details when displayed using the rescaled coordinate,
$0.711 \leq {\rm \Delta} \bar N\leq 0.714$, over a wide range of parameters, as seen in figure 14. The boundary-layer thickness (4.7) depends on details of the contact interactions between particles, as shown in figures 8 and 9; however, the particle distributions are almost independent of these details when displayed using the rescaled coordinate, ![]() $X_2/X_c$.
$X_2/X_c$.

Figure 14. Average deficit of particle density in the boundary layer (3.27) for monodisperse suspensions of particles with roughness ![]() $\delta =d/a$ (solid line) and drops with viscosity ratio
$\delta =d/a$ (solid line) and drops with viscosity ratio ![]() $\lambda$ (dashed line).
$\lambda$ (dashed line).
The above observation motivates a polynomial fit of the exact calculations. Enforcing continuity up to second derivatives at ![]() $y=\pm 1$, consistent with the expected continuity, discussed below (3.25a,b), and a prescribed value of the particle density deficit
$y=\pm 1$, consistent with the expected continuity, discussed below (3.25a,b), and a prescribed value of the particle density deficit ![]() ${\rm \Delta} \bar N$ yields
${\rm \Delta} \bar N$ yields
 \begin{equation} \bar N\doteq \left\{\begin{array}{@{}ll} 1+t+\dfrac{5}{2}t^2+35(3-4{\rm \Delta}\bar N) t^3 & \lvert \tilde y\rvert < 1\\ \lvert \tilde y\rvert^{{-}1/2} & \lvert \tilde y\rvert > 1 \end{array}\right. , \end{equation}
\begin{equation} \bar N\doteq \left\{\begin{array}{@{}ll} 1+t+\dfrac{5}{2}t^2+35(3-4{\rm \Delta}\bar N) t^3 & \lvert \tilde y\rvert < 1\\ \lvert \tilde y\rvert^{{-}1/2} & \lvert \tilde y\rvert > 1 \end{array}\right. , \end{equation}
where ![]() $t=\frac {1}{4}(1-\tilde y^2)$ and
$t=\frac {1}{4}(1-\tilde y^2)$ and ![]() $\tilde y=X_2/H$. Inserting the value of
$\tilde y=X_2/H$. Inserting the value of ![]() ${\rm \Delta} \bar N$ from figure 14 yields an approximation for
${\rm \Delta} \bar N$ from figure 14 yields an approximation for ![]() $\bar N$ with
$\bar N$ with ![]() $0.2\,\%$ maximum pointwise relative error; using the nominal value,
$0.2\,\%$ maximum pointwise relative error; using the nominal value, ![]() ${\rm \Delta} \bar N\doteq 0.71$, yields an approximation error of less than 1 % for most values of roughness or viscosity ratio. Given its accuracy, the polynomial fit is appropriate for use with the (less accurate) superposition approximation.
${\rm \Delta} \bar N\doteq 0.71$, yields an approximation error of less than 1 % for most values of roughness or viscosity ratio. Given its accuracy, the polynomial fit is appropriate for use with the (less accurate) superposition approximation.
An outline of the diffusive flux model is provided in Appendix B. For the purpose of comparing the dilute theory with the diffusive flux model (Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992), we employ its frequently used approximate solution (Koh et al. Reference Koh, Hookham and Leal1994)
where ![]() $\phi _{m}$ is the maximum packing fraction at the centreline of the channel, herein taken as
$\phi _{m}$ is the maximum packing fraction at the centreline of the channel, herein taken as ![]() $\phi _{m}=0.68$ following Koh et al. (Reference Koh, Hookham and Leal1994), and
$\phi _{m}=0.68$ following Koh et al. (Reference Koh, Hookham and Leal1994), and ![]() $\alpha$ is a numerical coefficient adjusted to enforce the bulk particle concentration (3.13). The prediction
$\alpha$ is a numerical coefficient adjusted to enforce the bulk particle concentration (3.13). The prediction ![]() $\phi =\phi _{m}$ at the centreline is a consequence of using a suspension viscosity model as explained in Appendix B but is inappropriate for dilute suspensions. Moreover, the cusp-shape profile is unphysical and the corresponding absence of a particle scale is at odds with experiments (Koh et al. Reference Koh, Hookham and Leal1994).
$\phi =\phi _{m}$ at the centreline is a consequence of using a suspension viscosity model as explained in Appendix B but is inappropriate for dilute suspensions. Moreover, the cusp-shape profile is unphysical and the corresponding absence of a particle scale is at odds with experiments (Koh et al. Reference Koh, Hookham and Leal1994).
The results in figures 15–17 show that the dilute theory is in approximate agreement with experiments for dilute suspensions and avoids the centreline cusp characteristic of the diffusive flux model. Empirical support for the predicted volume fraction and particle size dependence of the dilute theory is discussed in § 5.3.

Figure 15. Particle distribution in monodisperse suspension with roughness ![]() $\delta =d/a=10^{-2}$, bulk volume fraction
$\delta =d/a=10^{-2}$, bulk volume fraction ![]() $\phi _{\infty }=10\,\%$ and channel width
$\phi _{\infty }=10\,\%$ and channel width ![]() $H/a=8.8$. Dilute theory (3.26) (solid line); classical diffusive flux model (5.6) (dashed line); data from Koh et al. (Reference Koh, Hookham and Leal1994),
$H/a=8.8$. Dilute theory (3.26) (solid line); classical diffusive flux model (5.6) (dashed line); data from Koh et al. (Reference Koh, Hookham and Leal1994), ![]() $L_{exp}/L_{ss}=5.0$ (
$L_{exp}/L_{ss}=5.0$ (![]() $\bigcirc$).
$\bigcirc$).

Figure 16. Same as figure 15 except ![]() $H/a=15.6$; data (Koh et al. Reference Koh, Hookham and Leal1994)
$H/a=15.6$; data (Koh et al. Reference Koh, Hookham and Leal1994) ![]() $L_{exp}/L_{ss}=1.6$ (
$L_{exp}/L_{ss}=1.6$ (![]() $\bigcirc$).
$\bigcirc$).

Figure 17. Same as figure 15 except ![]() $\phi _{\infty }=20\,\%$; data (Koh et al. Reference Koh, Hookham and Leal1994)
$\phi _{\infty }=20\,\%$; data (Koh et al. Reference Koh, Hookham and Leal1994) ![]() $L_{exp}/L_{ss}=10.$ (
$L_{exp}/L_{ss}=10.$ (![]() $\bigcirc$).
$\bigcirc$).
5.2. Particle distribution in bidisperse suspensions
Results for bidisperse suspensions are presented here, including particle distributions, obtained by exact calculation and by superposition, and a parametric exploration of polydisperse enrichment due to the interactions between particles of different sizes. Predicted particle distributions are compared with the experiments of Lyon & Leal (Reference Lyon and Leal1998b) in bidisperse suspensions.
The bidisperse particle distributions shown in figure 18 show that small particles are enriched relative to large particles at the centreline, consistent with the approximately inverse square-root size dependence of the centreline density, discussed below (3.32). When rescaled using superposition variables (3.30a) and (3.31a), the distributions for both particles approximately collapse onto a universal distribution given by (5.5), as seen in figure 19.

Figure 18. Particle distributions ![]() $\bar N_i$ (
$\bar N_i$ (![]() $i=1,2$) in bidisperse suspensions with bulk volume fractions,
$i=1,2$) in bidisperse suspensions with bulk volume fractions, ![]() $\phi _{1\infty }=\phi _{2\infty }$; rough particles
$\phi _{1\infty }=\phi _{2\infty }$; rough particles ![]() $\delta _1=d/a_1=10^{-3}$, size ratio
$\delta _1=d/a_1=10^{-3}$, size ratio ![]() $\kappa =a_2/a_1=0.6$ (a),
$\kappa =a_2/a_1=0.6$ (a), ![]() $\kappa =0.8$ (b); drops with viscosity ratio
$\kappa =0.8$ (b); drops with viscosity ratio ![]() $\lambda =1$,
$\lambda =1$, ![]() $\kappa =1/2$ (c); numerical solution of (3.9) and (3.18) for large (thick solid line) and small (thin solid line) particles; superposition approximation (3.31a) (dashed lines), outer solution (3.12) (dotted lines).
$\kappa =1/2$ (c); numerical solution of (3.9) and (3.18) for large (thick solid line) and small (thin solid line) particles; superposition approximation (3.31a) (dashed lines), outer solution (3.12) (dotted lines).
Polydisperse enrichment (3.33) is a measure of the effect of interactions between particles of different sizes, an effect ignored by the superposition approximation. According to the discussion in § 3.2.3 and the remark at the end of § 4.4, the superposition approximation is expected to apply in bidisperse suspensions for ![]() $\kappa \lesssim \kappa ^*$ and for
$\kappa \lesssim \kappa ^*$ and for ![]() $\kappa \approx 1$, as confirmed by the results presented in figures 20 and 21 which show
$\kappa \approx 1$, as confirmed by the results presented in figures 20 and 21 which show ![]() ${\rm \Delta} \bar N_{ij}\to 0$ in these limits. Particle roughness
${\rm \Delta} \bar N_{ij}\to 0$ in these limits. Particle roughness ![]() $\delta _1$ and viscosity ratio
$\delta _1$ and viscosity ratio ![]() $\lambda$ determine the collision cross-section and thus the critical size ratio
$\lambda$ determine the collision cross-section and thus the critical size ratio ![]() $\kappa ^*$ below which contact interactions are not predicted.
$\kappa ^*$ below which contact interactions are not predicted.

Figure 20. Polydisperse enrichment (3.33) for large (thick lines) and small (thin lines) particles, ![]() $\phi _{2\infty }/\phi _{1\infty }$ as indicated; (a) particles with roughness
$\phi _{2\infty }/\phi _{1\infty }$ as indicated; (a) particles with roughness ![]() $\delta _1=d/a_1=10^{-3}$, (b) drops with viscosity ratio
$\delta _1=d/a_1=10^{-3}$, (b) drops with viscosity ratio ![]() $\lambda =1$.
$\lambda =1$.

Figure 21. Polydisperse enrichment (3.33) for large (thick lines) and small (thin lines) particles, ![]() $\phi _{2\infty }/\phi _{1\infty }=1$; (a) particles, roughness
$\phi _{2\infty }/\phi _{1\infty }=1$; (a) particles, roughness ![]() $\delta _1=d/a_1$ as indicated; (b) drops,
$\delta _1=d/a_1$ as indicated; (b) drops, ![]() $\lambda$ as indicated.
$\lambda$ as indicated.
The results in figures 20 and 21 demonstrate that the superposition approximation provides an estimate of the particle distribution for all size ratios (examples for intermediate size ratio are shown in figure 18). The weak coupling for all size ratios is likely due to the absence of coupling outside the boundary layer, as discussed in § 3.2.3. For rough particles, the superposition approximation is accurate to within a few per cent for a broad range of parameters; larger errors occur for emulsion drops because the displacements resulting from collisions between unequal drops exceed those for unequal rough particles, as seen by comparing figures 10(a) and 11(a).
Polydisperse enrichment in binary suspensions is most sensitive to size ratio. Polydisperse enrichment of larger particles is predicted for rough particles at all size ratios, as seen in panel (a) of figures 20 and 21, whereas smaller particles are enriched by the presence of much larger particles (small size ratios) and depleted by the presence of moderately larger particles. The particle distributions in panels (a) and (b) of figures 18 and 19 illustrate both regimes. By contrast, a polydisperse depletion of larger drops and enhancement of smaller drops is predicted for emulsions over most of the parameter range, as seen in panel (b) of figures 20 and 21. Panel (c) of figures 18 and 19 illustrates a typical drop distribution and shows the bigger effect of polydispersity.
The bulk composition, ![]() $\phi _{2\infty }/\phi _{1\infty }$, modulates the magnitude of polydisperse enrichment and depletion in suspensions of particles and drops but has less effect on whether it occurs, according to the results shown in figure 20. The viscosity ratio
$\phi _{2\infty }/\phi _{1\infty }$, modulates the magnitude of polydisperse enrichment and depletion in suspensions of particles and drops but has less effect on whether it occurs, according to the results shown in figure 20. The viscosity ratio ![]() $\lambda$ also modulates the magnitude of polydisperse enrichment and depletion as seen in figure 21(b). Particle roughness has a weaker effect on the magnitude of polydisperse enrichment and depletion; figure 21(a) shows that the polydisperse enrichment of large particles is insensitive to roughness.
$\lambda$ also modulates the magnitude of polydisperse enrichment and depletion as seen in figure 21(b). Particle roughness has a weaker effect on the magnitude of polydisperse enrichment and depletion; figure 21(a) shows that the polydisperse enrichment of large particles is insensitive to roughness.
Figures 22 and 23 show particle distributions in bidisperse suspensions with 30 % volume fraction. The dilute theory quantitatively predicts the distribution of large particles in the experiments of Lyon & Leal (Reference Lyon and Leal1998b), except near the boundary, ![]() $\lvert X_2\rvert /H\geq 0.8$, where the data are reported to be unreliable (Lyon & Leal Reference Lyon and Leal1998b). Here, the superposition approximation of the dilute theory is used. Similarly, assuming independent transport of large particles, the authors fit their results for large particles using the suspension balance model for a monodisperse suspension (Morris & Brady Reference Morris and Brady1998).
$\lvert X_2\rvert /H\geq 0.8$, where the data are reported to be unreliable (Lyon & Leal Reference Lyon and Leal1998b). Here, the superposition approximation of the dilute theory is used. Similarly, assuming independent transport of large particles, the authors fit their results for large particles using the suspension balance model for a monodisperse suspension (Morris & Brady Reference Morris and Brady1998).

Figure 22. Particle distribution in bidisperse suspension with size ratio, ![]() $\kappa =a_2/a_1=0.3$, roughness
$\kappa =a_2/a_1=0.3$, roughness ![]() $\delta _1=d/a_1=10^{-2}$, bulk volume fractions
$\delta _1=d/a_1=10^{-2}$, bulk volume fractions ![]() $\phi _1=22.5\,\%$ and
$\phi _1=22.5\,\%$ and ![]() $\phi _2=7.5\,\%$, channel width
$\phi _2=7.5\,\%$, channel width ![]() $H/a_1=11$; dilute theory with superposition approximation (3.29) for large (thick line) and small (thin line) particles; data from Lyon & Leal (Reference Lyon and Leal1998b) large (
$H/a_1=11$; dilute theory with superposition approximation (3.29) for large (thick line) and small (thin line) particles; data from Lyon & Leal (Reference Lyon and Leal1998b) large (![]() $\triangle$) and small (
$\triangle$) and small (![]() $\bigcirc$) particles,
$\bigcirc$) particles, ![]() $L_{exp}/L_{1_{ss}}=5.0$,
$L_{exp}/L_{1_{ss}}=5.0$, ![]() $L_{exp}/L_{2_{ss}}=0.14$.
$L_{exp}/L_{2_{ss}}=0.14$.

Figure 23. Same as figure 22, except for ![]() $\phi _1=\phi _2=15\,\%$; data (Lyon & Leal Reference Lyon and Leal1998b) large (
$\phi _1=\phi _2=15\,\%$; data (Lyon & Leal Reference Lyon and Leal1998b) large (![]() $\triangle$) and small (
$\triangle$) and small (![]() $\bigcirc$) particles,
$\bigcirc$) particles, ![]() $L_{exp}/L_{1_{ss}}=3.3$,
$L_{exp}/L_{1_{ss}}=3.3$, ![]() $L_{exp}/L_{2_{ss}}=0.28$.
$L_{exp}/L_{2_{ss}}=0.28$.
By contrast, the experiments depicted in figures 22 and 23 show essentially no flow-induced structuring of small particles; however, this is likely due to insufficient entry length to achieve the stationary distribution of small particles, as suggested by the authors (Lyon & Leal Reference Lyon and Leal1998b). As indicated in the figure captions, the entry length used in the experiments, ![]() $L_{exp}$, is at least 3.5 times shorter than the estimated length,
$L_{exp}$, is at least 3.5 times shorter than the estimated length, ![]() $L_{2_{ss}}$, required to establish a stationary distribution of the smaller particles. The slow evolution of particle microstructure is well known (Nott & Brady Reference Nott and Brady1994; Phan-Thien & Fang Reference Phan-Thien and Fang1996; Lyon & Leal Reference Lyon and Leal1998a); however, the hypothesis that particles of different sizes have distinct entry lengths has received less consideration (Semwogerere & Weeks Reference Semwogerere and Weeks2008). The experiments reported by Lyon & Leal (Reference Lyon and Leal1998b), including data not shown here, are consistent with distinct entry lengths predicted by (5.3).
$L_{2_{ss}}$, required to establish a stationary distribution of the smaller particles. The slow evolution of particle microstructure is well known (Nott & Brady Reference Nott and Brady1994; Phan-Thien & Fang Reference Phan-Thien and Fang1996; Lyon & Leal Reference Lyon and Leal1998a); however, the hypothesis that particles of different sizes have distinct entry lengths has received less consideration (Semwogerere & Weeks Reference Semwogerere and Weeks2008). The experiments reported by Lyon & Leal (Reference Lyon and Leal1998b), including data not shown here, are consistent with distinct entry lengths predicted by (5.3).
There have been few studies that measure polydisperse enrichment, i.e. deviations from superposition resulting from hydrodynamic interactions between particles of different size. Semwogerere & Weeks (Reference Semwogerere and Weeks2008) observed polydisperse enrichment of large or small particles at the centreline and suggested that particles with a shorter entry length become more enriched in the centre region. Their results are less relevant here because colloidal (Brownian) particles were used in their study.
The experiments shown in figures 22 and 23 have been compared with a bidisperse diffusive flux model (Shauly et al. Reference Shauly, Wachs and Nir1998; Chun et al. Reference Chun, Park, Jung and Won2019). In planar Poiseuille flow, the bidisperse diffusive flux model predicts cusp-shaped distributions of both particle species: an upward cusp for the larger particles with a prescribed maximum volume fraction at the centreline, and a downward cusp for smaller particles with zero concentration at the centreline. By adjusting the physical parameters (size ratio, volume fractions and channel width), it was shown that the distribution of large particles could be made to fit the data but the predictions for the small particles were found to be qualitatively at odds with observations (Lyon & Leal Reference Lyon and Leal1998b; Chun et al. Reference Chun, Park, Jung and Won2019).
5.3. Limitation of dilute theory
Here, we propose a volume fraction criterion for application of the dilute theory. Data aggregated from several experiments that satisfy this criterion and the required entry length (5.4) are used to further validate the dilute theory.
At larger volume fractions, the dilute theory fails by predicting a centreline volume fraction above the maximum packing limit. This observation provides a rough practical upper bound of the bulk particle volume fraction ![]() $\phi ^*_\infty$ in a monodisperse suspension and an upper bound
$\phi ^*_\infty$ in a monodisperse suspension and an upper bound ![]() $\phi ^*_{i\infty }$ for each particle species in a polydisperse suspension. Using the superposition approximation (3.29) with polynomial fit (5.5), and setting the centreline particle volume fraction equal to the maximum packing limit,
$\phi ^*_{i\infty }$ for each particle species in a polydisperse suspension. Using the superposition approximation (3.29) with polynomial fit (5.5), and setting the centreline particle volume fraction equal to the maximum packing limit, ![]() $\phi (0)=\phi _{m}$, we obtain
$\phi (0)=\phi _{m}$, we obtain
where ![]() $\epsilon _i$ is defined by (3.30b), and dropping the index
$\epsilon _i$ is defined by (3.30b), and dropping the index ![]() $i$ for monodisperse suspensions. For particles with
$i$ for monodisperse suspensions. For particles with ![]() $1\,\%$ roughness,
$1\,\%$ roughness, ![]() $X_c^{ii}\doteq 0.52 a_i$, yielding the upper bound
$X_c^{ii}\doteq 0.52 a_i$, yielding the upper bound ![]() $\phi _{i \infty }^*/\phi _{m} \approx 1.16\, (a_i/H)^{1/2}$. Taking
$\phi _{i \infty }^*/\phi _{m} \approx 1.16\, (a_i/H)^{1/2}$. Taking ![]() $\phi _{m}=0.68$, we find
$\phi _{m}=0.68$, we find ![]() $\phi _\infty ^* \approx 27\,\%$ for the conditions described in figures 15 and 17, and
$\phi _\infty ^* \approx 27\,\%$ for the conditions described in figures 15 and 17, and ![]() $\phi _\infty ^* \approx$ 20 % for those in figure 16. For the conditions in figures 22 and 23, we have
$\phi _\infty ^* \approx$ 20 % for those in figure 16. For the conditions in figures 22 and 23, we have ![]() $\phi _{1 \infty }^* \approx 24\,\%$ and
$\phi _{1 \infty }^* \approx 24\,\%$ and ![]() $\phi _{2 \infty }^* \approx 13\,\%$ but a smaller value may be warranted to accommodate a smaller value for
$\phi _{2 \infty }^* \approx 13\,\%$ but a smaller value may be warranted to accommodate a smaller value for ![]() $\phi _{m}$.
$\phi _{m}$.
All experiments from Koh et al. (Reference Koh, Hookham and Leal1994) and Lyon & Leal (Reference Lyon and Leal1998a) that satisfy constraint (5.7) and have the required entry length (5.4) are aggregated in figure 24, omitting data close to the wall, ![]() $\lvert X_2\rvert /H\geq 0.8$, as suggested by Lyon & Leal (Reference Lyon and Leal1998b). According to (3.29), these data should collapse onto a single curve when re-plotted using
$\lvert X_2\rvert /H\geq 0.8$, as suggested by Lyon & Leal (Reference Lyon and Leal1998b). According to (3.29), these data should collapse onto a single curve when re-plotted using
where ![]() $\epsilon _i$ is given by (3.30b) and
$\epsilon _i$ is given by (3.30b) and ![]() $f(x)$ is defined by (3.28) with
$f(x)$ is defined by (3.28) with ![]() ${\rm \Delta} \bar N\doteq 0.71$. The index
${\rm \Delta} \bar N\doteq 0.71$. The index ![]() $i$ is dropped for monodisperse suspensions. As shown in figure 25, the data approximately collapse according to the dilute theory (and superposition approximation for bidisperse systems) when re-plotted this way.
$i$ is dropped for monodisperse suspensions. As shown in figure 25, the data approximately collapse according to the dilute theory (and superposition approximation for bidisperse systems) when re-plotted this way.

Figure 24. Data for monodisperse suspensions from Koh et al. (Reference Koh, Hookham and Leal1994) ![]() $\phi =10\,\%,\ H/a=8.8, L_{exp}/L_{ss}=5.0$ (
$\phi =10\,\%,\ H/a=8.8, L_{exp}/L_{ss}=5.0$ (![]() $\bigcirc$),
$\bigcirc$), ![]() $H/a=15.6, L_{exp}/L_{ss}=1.6$ (
$H/a=15.6, L_{exp}/L_{ss}=1.6$ (![]() $\square$);
$\square$); ![]() $\phi =20\,\% , H/a=8.8, L_{exp}/L_{ss}=10.$ (
$\phi =20\,\% , H/a=8.8, L_{exp}/L_{ss}=10.$ (![]() $\lozenge$),
$\lozenge$), ![]() $H/a=15.6, L_{exp}/L_{ss}=3.2$ (
$H/a=15.6, L_{exp}/L_{ss}=3.2$ (![]() $\triangledown$). Data for large particles in bidisperse suspensions from Lyon & Leal (Reference Lyon and Leal1998b)
$\triangledown$). Data for large particles in bidisperse suspensions from Lyon & Leal (Reference Lyon and Leal1998b) ![]() $H/a_1=11, \phi _1=7.5\,\% , L_{exp}/L_{1_{ss}}=1.7$ (
$H/a_1=11, \phi _1=7.5\,\% , L_{exp}/L_{1_{ss}}=1.7$ (![]() $\blacktriangle$),
$\blacktriangle$), ![]() $\phi _1=10\,\% , L_{exp}/L_{1_{ss}}=2.2$ (
$\phi _1=10\,\% , L_{exp}/L_{1_{ss}}=2.2$ (![]() $\blacksquare$),
$\blacksquare$), ![]() $\phi _1=15\,\% , L_{exp}/L_{1_{ss}}=3.3$ (
$\phi _1=15\,\% , L_{exp}/L_{1_{ss}}=3.3$ (![]() $\blacktriangledown$),
$\blacktriangledown$), ![]() $\phi _1=20\,\% , L_{exp}/L_{1_{ss}}=4.4$ (
$\phi _1=20\,\% , L_{exp}/L_{1_{ss}}=4.4$ (![]() $\mathbin {\blacklozenge }$),
$\mathbin {\blacklozenge }$), ![]() $\phi _1=22.5\,\% , L_{exp}/L_{1_{ss}}=5$ (
$\phi _1=22.5\,\% , L_{exp}/L_{1_{ss}}=5$ (![]() $\bullet$).
$\bullet$).
The collapse of data for large particles in bidisperse suspensions (filled symbols) demonstrates the proportionality to bulk volume fraction because these data differ only in volume fraction. This is also seen in the collapse of data for monodisperse suspensions with 10 % and 20 % volume fractions with the same size particles (compare data points ![]() $\bigcirc$ with
$\bigcirc$ with ![]() $\lozenge$ and
$\lozenge$ and ![]() $\square$ with
$\square$ with ![]() $\triangledown$). Validation for the size dependence predicted by the dilute theory is seen by comparing data for suspensions with different sized particles at fixed volume fractions (compare
$\triangledown$). Validation for the size dependence predicted by the dilute theory is seen by comparing data for suspensions with different sized particles at fixed volume fractions (compare ![]() $\bigcirc$ with
$\bigcirc$ with ![]() $\square$ and
$\square$ and ![]() $\lozenge$ with
$\lozenge$ with ![]() $\triangledown$).
$\triangledown$).
Although the data are seen to collapse when re-plotted according to (5.8) in figure 25, the shape of the universal curve (solid line) is not accurately obtained. We note that the data for large particles from Lyon & Leal (Reference Lyon and Leal1998b) (filled symbols) appear to attain the shape of the universal curve more closely than the data from Koh et al. (Reference Koh, Hookham and Leal1994) (open symbols), consistent with the closer, quantitative agreement seen in figures 22 and 23 compared with that seen in figures 15–17. Systematic errors in the earlier study, discussed by Lyon & Leal (Reference Lyon and Leal1998a), might account for this difference.
6. Conclusions
In this work we present a pairwise theory for particle distributions in dilute suspensions undergoing two-dimensional unidirectional flows, including planar Poiseuille and shear flows. There are no adjustable parameters.
A boundary layer is shown to form where the shear rate vanishes at the centre of Poiseuille flow; its thickness is set by the maximum of particle-related scales, including collision cross-sections, and net pairwise particle displacements. Size segregation occurs in the boundary layer leading to enrichment of smaller particles. Centreline particle densities scale approximately with the inverse square root of particle size. The finding of linearly vanishing drift velocities and non-vanishing diffusive fluxes in the boundary layer avoids the singular distribution predicted by other models. Outside of the boundary layer, particle distributions for each particle species are decoupled, independent of particle size, and obey a power law with exponent ![]() $-\beta /2$ in a power-law shear rate with exponent
$-\beta /2$ in a power-law shear rate with exponent ![]() $\beta$. These results hold for systems with arbitrary symmetry-breaking pair interactions between particles.
$\beta$. These results hold for systems with arbitrary symmetry-breaking pair interactions between particles.
Pair displacements for hydrodynamically interacting particles that undergo symmetry-breaking contact interactions were reduced to quadratures of mobility functions for spherical particles or drops. This result qualitatively advances the computational efficiency of calculations for particle distributions, making feasible an exploration of the three-dimensional parameter space that describes particle distributions in bidisperse suspensions, including size ratio, bulk composition and parameters that characterize particle interactions. Specific calculations were performed for rough particles and permeable particles (via an established equivalence relation) and for non-coalescing spherical drops.
After rescaling by the collision cross-section, particle distributions in monodisperse suspensions have an almost universal shape, nearly independent of particle roughness or drop viscosity. Polydisperse enrichment and depletion in bidisperse suspensions due to the coupling between particles of different sizes enhances the centreline concentration of large particles for the entire parameter space, whereas small particles are enriched for smaller size ratios and depleted for larger. By contrast, drops with mobile interfaces generally show polydisperse centreline enrichment of smaller drops and depletion of larger ones. Polydisperse enrichment is a comparatively weak effect, however, probably resulting from the absence of coupling between particle distributions outside the boundary layer. This allows particle distributions in polydisperse suspensions to be approximately described by a superposition of monodisperse distributions.
Within its limitations, the dilute theory is shown to be in agreement with available experiments for moderately dilute suspensions of non-Brownian particles. The predicted dependence on the bulk volume fraction and particle size are supported by these results. The experiments moreover support the superposition approximation. Some of the discrepancy between experiments and theory is likely the use of inadequate entry lengths. A transient analysis of particle distributions will help to confirm the theory. The superposition approximation may breakdown in smaller channels with significant size-dependent wall migration.
Funding
This work was supported by the National Science Foundation (grant number 1603806) and the Coordenaçõo de Aperfeiçoamento de Pessoal de Nível Superior - Brasil (Capes) (Finance Code 001).
Declaration of interests
The authors report no conflict of interest.
Appendix A. Derivation of transport coefficients in planar Poiseuille flows
In this section, we present a derivation of the transport coefficients in the velocity-gradient direction in regions where the shear rate vanishes. Inserting the exact relative particle velocity magnitude (2.34) into the particle flux integral (2.4), and transforming to the cylindrical coordinate system shown in figure 2, yields
 \begin{align} F_{ij2}(X_2)&=\dot{\gamma}'_2 \int_{0}^{2{\rm \pi}} \int_{0}^{r_c^{ij}} r^{-\infty} \lvert \sin \theta \rvert \left[ \int_{-{\rm \Delta} X^{ij}_{2}}^{0} n_{i}(X^{i,-\infty}_{2})n_{j}(X^{j,-\infty}_{2}) \right. \nonumber\\ & \quad \left. \left \lvert X_{2}+X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta \right \rvert \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty}\, {\rm d} r^{-\infty} \, {\rm d} \theta. \end{align}
\begin{align} F_{ij2}(X_2)&=\dot{\gamma}'_2 \int_{0}^{2{\rm \pi}} \int_{0}^{r_c^{ij}} r^{-\infty} \lvert \sin \theta \rvert \left[ \int_{-{\rm \Delta} X^{ij}_{2}}^{0} n_{i}(X^{i,-\infty}_{2})n_{j}(X^{j,-\infty}_{2}) \right. \nonumber\\ & \quad \left. \left \lvert X_{2}+X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta \right \rvert \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty}\, {\rm d} r^{-\infty} \, {\rm d} \theta. \end{align}
Here, ![]() $X^{i,-\infty }_{2}$ is the distance of particle-
$X^{i,-\infty }_{2}$ is the distance of particle-![]() $i$ from the plane
$i$ from the plane ![]() $X_2$ where the flux is measured and
$X_2$ where the flux is measured and ![]() $X^{j,-\infty }_{2}$ is the distance of particle-
$X^{j,-\infty }_{2}$ is the distance of particle-![]() $j$ from this plane, as depicted in figure 1.
$j$ from this plane, as depicted in figure 1.
We proceed by inserting linear variations in number density (2.13) into (A1) but the complete velocity field (2.34) is used here, not a linearized approximation, because the latter is inconsistent in the region where the shear rate vanishes. Splitting the angular ![]() $\theta$-integration in (A1) into two ranges:
$\theta$-integration in (A1) into two ranges: ![]() $0\leq \theta < {\rm \pi}$ and
$0\leq \theta < {\rm \pi}$ and ![]() ${\rm \pi} \leq \theta < 2{\rm \pi}$, and using the symmetry relation (2.7) to consolidate integration to the range
${\rm \pi} \leq \theta < 2{\rm \pi}$, and using the symmetry relation (2.7) to consolidate integration to the range ![]() $0\leq \theta < {\rm \pi}$ yields
$0\leq \theta < {\rm \pi}$ yields
 \begin{align} I^{(1)}_{ij}(X_2)&=\frac{1}{2}\frac{1}{\lvert X_2 \rvert}\int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int^{-{\rm \Delta} X^{ij}_{2}}_{0} \left(\left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta -X_{2} \right\rvert \right. \right. \nonumber\\ &\quad \left. \left. + \left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta+X_{2} \right\rvert\right) X^{i,-\infty}_{2} \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta, \end{align}
\begin{align} I^{(1)}_{ij}(X_2)&=\frac{1}{2}\frac{1}{\lvert X_2 \rvert}\int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int^{-{\rm \Delta} X^{ij}_{2}}_{0} \left(\left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta -X_{2} \right\rvert \right. \right. \nonumber\\ &\quad \left. \left. + \left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta+X_{2} \right\rvert\right) X^{i,-\infty}_{2} \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta, \end{align} \begin{align} I^{(2)}_{ij}(X_2)&=\frac{1}{2}\frac{1}{\lvert X_2 \rvert} \int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int^{-{\rm \Delta} X^{ij}_{2}}_{0} \left(\left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta -X_{2} \right \rvert \right. \right. \nonumber\\ &\quad \left. \left. + \left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta+X_{2} \right \rvert\right) \right. \nonumber\\ &\quad \left. \vphantom{\int_{0}^{r_c^{ij}}} (r^{-\infty}\sin \theta +X^{i,-\infty}_{2} ) \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
\begin{align} I^{(2)}_{ij}(X_2)&=\frac{1}{2}\frac{1}{\lvert X_2 \rvert} \int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int^{-{\rm \Delta} X^{ij}_{2}}_{0} \left(\left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta -X_{2} \right \rvert \right. \right. \nonumber\\ &\quad \left. \left. + \left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta+X_{2} \right \rvert\right) \right. \nonumber\\ &\quad \left. \vphantom{\int_{0}^{r_c^{ij}}} (r^{-\infty}\sin \theta +X^{i,-\infty}_{2} ) \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}and
 \begin{align} I^{(3)}_{ij}(X_2)&=\frac{1}{2}\int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int^{-{\rm \Delta} X^{ij}_{2}}_{0} \left(\left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta -X_{2} \right \rvert \right. \right. \nonumber\\ & \quad \left. \left. - \left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta+X_{2} \right \rvert\right) \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
\begin{align} I^{(3)}_{ij}(X_2)&=\frac{1}{2}\int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int^{-{\rm \Delta} X^{ij}_{2}}_{0} \left(\left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta -X_{2} \right \rvert \right. \right. \nonumber\\ & \quad \left. \left. - \left \lvert X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty}\sin \theta+X_{2} \right \rvert\right) \, {\rm d} X^{i,-\infty}_{2}\right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
where ![]() $-{\rm \Delta} X^{ij}_2 > 0$ according to (2.49).
$-{\rm \Delta} X^{ij}_2 > 0$ according to (2.49).
Equations (A2)–(A4) indicate that integrals ![]() $I^{(1)}(X_2)$ and
$I^{(1)}(X_2)$ and ![]() $I^{(2)}(X_2)$ are even functions and
$I^{(2)}(X_2)$ are even functions and ![]() $I^{(3)}(X_2)$ is an odd function of
$I^{(3)}(X_2)$ is an odd function of ![]() $X_2$. Accordingly, we can make the replacement
$X_2$. Accordingly, we can make the replacement ![]() $X_2\to \lvert X_2\rvert$ in these equations without other changes, except multiplying (A4) by sign
$X_2\to \lvert X_2\rvert$ in these equations without other changes, except multiplying (A4) by sign![]() $(X_2)$. After so doing, the absolute value can be removed from the second term in each integrand because its argument,
$(X_2)$. After so doing, the absolute value can be removed from the second term in each integrand because its argument, ![]() $X^{i,-\infty }_{2}+\frac {1}{2}r^{-\infty }\sin \theta +\lvert X_{2}\rvert$, is intrinsically positive for
$X^{i,-\infty }_{2}+\frac {1}{2}r^{-\infty }\sin \theta +\lvert X_{2}\rvert$, is intrinsically positive for ![]() $0 < \theta < {\rm \pi}$. However, removing the absolute value of the first term of each integrand requires splitting the range of the
$0 < \theta < {\rm \pi}$. However, removing the absolute value of the first term of each integrand requires splitting the range of the ![]() $X^{i,-\infty }_{2}$ integration in two intervals,
$X^{i,-\infty }_{2}$ integration in two intervals,
and
where ![]() $X_2'$ is defined by (2.47) and
$X_2'$ is defined by (2.47) and ![]() $B(x)$ is the ramp function (2.48). After implementing the foregoing manoeuvres, integrals (A2)–(A4) become
$B(x)$ is the ramp function (2.48). After implementing the foregoing manoeuvres, integrals (A2)–(A4) become
 \begin{align} I^{(1)}_{ij}(X_2) &=\frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int_{0}^{-{\rm \Delta} X^{ij}_2 B(X_2')}\vert X_2\vert X^{i,-\infty}_{2} \, {\rm d} X^{i,-\infty}_{2}\right. \nonumber\\ &\quad \left.+\int_{-{\rm \Delta} X^{ij}_2 B(X_2')}^{-{\rm \Delta} X^{ij}_{2}} \left(X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty} \sin \theta\right) X^{i,-\infty}_{2} \, {\rm d} X^{i,-\infty}_{2} \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta, \end{align}
\begin{align} I^{(1)}_{ij}(X_2) &=\frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int_{0}^{-{\rm \Delta} X^{ij}_2 B(X_2')}\vert X_2\vert X^{i,-\infty}_{2} \, {\rm d} X^{i,-\infty}_{2}\right. \nonumber\\ &\quad \left.+\int_{-{\rm \Delta} X^{ij}_2 B(X_2')}^{-{\rm \Delta} X^{ij}_{2}} \left(X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty} \sin \theta\right) X^{i,-\infty}_{2} \, {\rm d} X^{i,-\infty}_{2} \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta, \end{align} \begin{align} I^{(2)}_{ij}(X_2) &= \frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int_{0}^{-{\rm \Delta} X^{ij}_2 B(X_2')} \vert X_2\vert(X^{i,-\infty}_{2}+r^{-\infty} \sin \theta)\, {\rm d} X^{i,-\infty}_{2}\right. \nonumber\\ &\quad \left.+\int_{-{\rm \Delta} X^{ij}_2 B(X_2')}^{-{\rm \Delta} X^{ij}_{2}} \left(X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty} \sin \theta\right)(X^{i,-\infty}_{2}+r^{-\infty} \sin \theta) \, {\rm d} X^{i,-\infty}_{2} \right]\nonumber\\ &\qquad\qquad r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align}
\begin{align} I^{(2)}_{ij}(X_2) &= \frac{1}{\vert X_2\vert} \int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int_{0}^{-{\rm \Delta} X^{ij}_2 B(X_2')} \vert X_2\vert(X^{i,-\infty}_{2}+r^{-\infty} \sin \theta)\, {\rm d} X^{i,-\infty}_{2}\right. \nonumber\\ &\quad \left.+\int_{-{\rm \Delta} X^{ij}_2 B(X_2')}^{-{\rm \Delta} X^{ij}_{2}} \left(X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty} \sin \theta\right)(X^{i,-\infty}_{2}+r^{-\infty} \sin \theta) \, {\rm d} X^{i,-\infty}_{2} \right]\nonumber\\ &\qquad\qquad r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta , \end{align} \begin{align} I^{(3)}_{ij}(X_2)&=\mbox{sign}(X_2)\,\int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int_{0}^{-{\rm \Delta} X^{ij}_2 B(X_2')} \left(X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty} \sin \theta\right)\, {\rm d} X^{i,-\infty}_{2} \right.\nonumber\\ &\quad \left. +\int_{-{\rm \Delta} X^{ij}_2 B(X_2')}^{-{\rm \Delta} X^{ij}_{2}} \vert X_2\vert \, {\rm d} X^{i,-\infty}_{2} \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta . \end{align}
\begin{align} I^{(3)}_{ij}(X_2)&=\mbox{sign}(X_2)\,\int_{0}^{\rm \pi} \int_{0}^{r_c^{ij}} r^{-\infty} \sin \theta \left[ \int_{0}^{-{\rm \Delta} X^{ij}_2 B(X_2')} \left(X^{i,-\infty}_{2}+\frac{1}{2}r^{-\infty} \sin \theta\right)\, {\rm d} X^{i,-\infty}_{2} \right.\nonumber\\ &\quad \left. +\int_{-{\rm \Delta} X^{ij}_2 B(X_2')}^{-{\rm \Delta} X^{ij}_{2}} \vert X_2\vert \, {\rm d} X^{i,-\infty}_{2} \right] r^{-\infty} \, {\rm d} r^{-\infty} \, {\rm d} \theta . \end{align}
In this form, the ![]() $X^{i,-\infty }_{2}$ integration can be performed to yield the desired result given by (2.44)–(2.46).
$X^{i,-\infty }_{2}$ integration can be performed to yield the desired result given by (2.44)–(2.46).
Appendix B. Diffusive flux model
For comparison purposes, a brief outline of the diffusive flux model (Phillips et al. Reference Phillips, Armstrong, Brown, Graham and Abbott1992) is presented here, including a local analysis of the predicted behaviour at the centreline of the flow. From (11) in Phillips et al. (Reference Phillips, Armstrong, Brown, Graham and Abbott1992), the stationary particle distribution is governed by
where ![]() $K_c$ and
$K_c$ and ![]() $K_\eta$ are dimensionless constants,
$K_\eta$ are dimensionless constants, ![]() $\gamma$ is the shear rate non-dimensionalized by
$\gamma$ is the shear rate non-dimensionalized by ![]() ${v}_0/H$,
${v}_0/H$, ![]() $\eta (\phi )$ is the particle-concentration-dependent viscosity of the suspension and primes denote derivatives with respect to
$\eta (\phi )$ is the particle-concentration-dependent viscosity of the suspension and primes denote derivatives with respect to ![]() $\tilde y=X_2/H$. By a momentum balance, the shear rate is given by
$\tilde y=X_2/H$. By a momentum balance, the shear rate is given by
Krieger's empirical model (Krieger Reference Krieger1972) for the suspension viscosity is used to complete the description
where ![]() $\eta _0$ is the viscosity of the continuous-phase liquid. Here,
$\eta _0$ is the viscosity of the continuous-phase liquid. Here, ![]() $\phi =\phi _{m}$ is the maximum packing fraction of the suspension, where the viscosity diverges, and
$\phi =\phi _{m}$ is the maximum packing fraction of the suspension, where the viscosity diverges, and ![]() $\beta \doteq 1.82$. Note that particle size does not enter the diffusive flux model.
$\beta \doteq 1.82$. Note that particle size does not enter the diffusive flux model.
The shear rate vanishes at the centreline but ![]() $\gamma '$ does not. According to (B1), a non-singular particle distribution requires divergence of the viscosity, thus
$\gamma '$ does not. According to (B1), a non-singular particle distribution requires divergence of the viscosity, thus ![]() $\phi \to \phi _{m}$ is required at
$\phi \to \phi _{m}$ is required at ![]() $\tilde y=0$. The solution of (B1)–(B3) has a cusp at the centreline,
$\tilde y=0$. The solution of (B1)–(B3) has a cusp at the centreline,
where ![]() $M_4$ is a positive constant determined by the solution away from the centre and the exponent is given by
$M_4$ is a positive constant determined by the solution away from the centre and the exponent is given by
Phillips et al. (Reference Phillips, Armstrong, Brown, Graham and Abbott1992) report ![]() $K_c/K_\eta \doteq 0.66$, thus
$K_c/K_\eta \doteq 0.66$, thus ![]() $c\approx 1$.
$c\approx 1$.
An approximate solution of (B1)–(B3) for planar Poiseuille flow (Koh et al. Reference Koh, Hookham and Leal1994), consistent with the local analysis above, is given by (5.6).
Appendix C. Analytical integration of contacting pair trajectories
Analytical integration formulas are derived here for contacting particle trajectories, such as those shown in figures 4 and 5. As illustrated, widely separated particles with upstream offsets within the collision cross-section are brought together by the imposed flow, reach the contact surface (ii), move along the contact surface in the compressional quadrant of the flow (ii–iii), separate at the edge of the compressional quadrant (iii) and again become widely separated. A contact force prevents particle overlap on the contact surface portion of trajectories (ii–iii). The relative and pair motion of the particles are separately treated. The former has been previously analysed in classical works as cited below; integration of the pair motion is new. Both are needed to determine particle displacements.
C.1. Particle trajectories
In a linear flow under creeping flow conditions, the trajectories of non-Brownian, neutrally buoyant, inertialess particles with labels 1 and 2 are described by Batchelor & Green (Reference Batchelor and Green1972b)
and
where, ![]() $\boldsymbol {r}=\boldsymbol {X}^{(2)}-\boldsymbol {X}^{(1)}$ is the vector between the particle centres, as shown in figure 26,
$\boldsymbol {r}=\boldsymbol {X}^{(2)}-\boldsymbol {X}^{(1)}$ is the vector between the particle centres, as shown in figure 26, ![]() $\boldsymbol {\hat r}=\boldsymbol {r}/\vert \boldsymbol {r}\vert$ is a unit vector along the line of centres,
$\boldsymbol {\hat r}=\boldsymbol {r}/\vert \boldsymbol {r}\vert$ is a unit vector along the line of centres, ![]() $\boldsymbol {I}$ is the identity tensor and
$\boldsymbol {I}$ is the identity tensor and ![]() $s=\vert \boldsymbol {r}\vert /\bar a$ is the centre-to-centre separation normalized by the average radius. The undisturbed particle velocities are
$s=\vert \boldsymbol {r}\vert /\bar a$ is the centre-to-centre separation normalized by the average radius. The undisturbed particle velocities are ![]() $\boldsymbol {V}_i^{(\infty )}=\boldsymbol {E}\boldsymbol {\cdot }\boldsymbol {X}^{({\rm i})} +{\boldsymbol \omega }\times \boldsymbol {X}^{({\rm i})}$ (
$\boldsymbol {V}_i^{(\infty )}=\boldsymbol {E}\boldsymbol {\cdot }\boldsymbol {X}^{({\rm i})} +{\boldsymbol \omega }\times \boldsymbol {X}^{({\rm i})}$ (![]() $i=1,2$), where
$i=1,2$), where ![]() $\boldsymbol {E}$ is the rate of strain, and
$\boldsymbol {E}$ is the rate of strain, and ![]() ${\boldsymbol \omega }$ is the angular velocity. In simple shear flow
${\boldsymbol \omega }$ is the angular velocity. In simple shear flow
 \begin{equation} \boldsymbol{E}= \dot{\gamma} \begin{pmatrix} 0 & 1/2 & 0 \\ 1/2 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \quad {\boldsymbol\omega} = \dot{\gamma} \begin{pmatrix} 0, & 0, & -1/2 \end{pmatrix}, \end{equation}
\begin{equation} \boldsymbol{E}= \dot{\gamma} \begin{pmatrix} 0 & 1/2 & 0 \\ 1/2 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}, \quad {\boldsymbol\omega} = \dot{\gamma} \begin{pmatrix} 0, & 0, & -1/2 \end{pmatrix}, \end{equation}
where ![]() $\dot {\gamma }$ is the magnitude of the local shear rate. In (C1) and (C2),
$\dot {\gamma }$ is the magnitude of the local shear rate. In (C1) and (C2), ![]() $A_{i}$ and
$A_{i}$ and ![]() $B_{i}$ (
$B_{i}$ (![]() $i=1,2$), respectively, are mobility functions that incorporate the effect of hydrodynamic interactions on the particle velocities parallel and normal to the line of centres of the pair. Mobility functions depend also on the particle size ratio
$i=1,2$), respectively, are mobility functions that incorporate the effect of hydrodynamic interactions on the particle velocities parallel and normal to the line of centres of the pair. Mobility functions depend also on the particle size ratio ![]() $\kappa =a_2/a_1$, and for spherical drops, also on the drop-to-continuous-phase viscosity ratio,
$\kappa =a_2/a_1$, and for spherical drops, also on the drop-to-continuous-phase viscosity ratio, ![]() $\lambda$.
$\lambda$.

Figure 26. Spherical coordinate system ![]() $(r,\theta,\phi )$ for pair trajectories, where
$(r,\theta,\phi )$ for pair trajectories, where ![]() $x_1=r\sin \theta \cos \phi$,
$x_1=r\sin \theta \cos \phi$, ![]() $x_2=r\sin \theta \sin \phi$,
$x_2=r\sin \theta \sin \phi$, ![]() $x_3=r\cos \theta$.
$x_3=r\cos \theta$.
C.2. Trajectory integration
The relative motion of the particles are described by the trajectory equations (Batchelor & Green Reference Batchelor and Green1972b)
where the spherical coordinates defined in figure 26 are used. The pair motion of the particles is described by
Here, ![]() $t$ is strain, and
$t$ is strain, and ![]() $\boldsymbol {x}$ and
$\boldsymbol {x}$ and ![]() $\boldsymbol {\bar x}$, respectively, are the relative and pair positions
$\boldsymbol {\bar x}$, respectively, are the relative and pair positions
Relative and pair mobilities are denoted ![]() $M=M_2-M_1$ and
$M=M_2-M_1$ and ![]() $M_p=M_1+M_2$, respectively, where
$M_p=M_1+M_2$, respectively, where ![]() $M=A$ or
$M=A$ or ![]() $B$. In prior analyses, only the relative mobilities were required (Batchelor & Green Reference Batchelor and Green1972a,Reference Batchelor and Greenb; Zinchenko Reference Zinchenko1978, Reference Zinchenko1980, Reference Zinchenko1983; Wilson Reference Wilson2005). Here, pair mobilities are also required because the displacements of both particles, not just their relative displacement, are needed. By symmetry, we can restrict our attention to relative positions
$B$. In prior analyses, only the relative mobilities were required (Batchelor & Green Reference Batchelor and Green1972a,Reference Batchelor and Greenb; Zinchenko Reference Zinchenko1978, Reference Zinchenko1980, Reference Zinchenko1983; Wilson Reference Wilson2005). Here, pair mobilities are also required because the displacements of both particles, not just their relative displacement, are needed. By symmetry, we can restrict our attention to relative positions ![]() $\boldsymbol {x}$ in the positive quarter-plane. Accordingly, the initial positions are
$\boldsymbol {x}$ in the positive quarter-plane. Accordingly, the initial positions are
but ![]() $\bar {\boldsymbol {x}}^{({\rm i})}$ is arbitrary because only differences of the pair position are significant.
$\bar {\boldsymbol {x}}^{({\rm i})}$ is arbitrary because only differences of the pair position are significant.
Integrating equations (C4)–(C6) with initial conditions (C11a) yields (Batchelor & Green Reference Batchelor and Green1972b; Zinchenko Reference Zinchenko1983)
where ![]() $x^{\infty }_{2}$ and
$x^{\infty }_{2}$ and ![]() $x^{\infty }_{3}$ are the cross-flow coordinates of the far-field relative position of the particles at
$x^{\infty }_{3}$ are the cross-flow coordinates of the far-field relative position of the particles at ![]() $s\to \infty$. The functions
$s\to \infty$. The functions ![]() $\varphi (s)$ and
$\varphi (s)$ and ![]() $\varPsi (s)$ are given by
$\varPsi (s)$ are given by
and
The minus sign applies in (C14) for ![]() ${\rm \pi} /2<\phi <{\rm \pi}$; the + sign applies for
${\rm \pi} /2<\phi <{\rm \pi}$; the + sign applies for ![]() $0<\phi <{\rm \pi} /2$.
$0<\phi <{\rm \pi} /2$.
Dividing equations (C8) and (C9) by (C4) and integrating yields the pair positions
and
where ![]() $\bar x^{\infty }_{2}$ and
$\bar x^{\infty }_{2}$ and ![]() $\bar x^{\infty }_{3}$ are the corresponding coordinates of the far-field pair position. The functions
$\bar x^{\infty }_{3}$ are the corresponding coordinates of the far-field pair position. The functions ![]() $\bar {\varphi }(s,x^{\infty }_{3})$ and
$\bar {\varphi }(s,x^{\infty }_{3})$ and ![]() $\bar {\varPsi }(s,x^{\infty }_{2})$ are defined
$\bar {\varPsi }(s,x^{\infty }_{2})$ are defined
and
where ![]() $x_{2}(s,x^{\infty }_{2})$ and
$x_{2}(s,x^{\infty }_{2})$ and ![]() $x_{3}(s,x^{\infty }_{3})$ are defined by (C12) and (C13). The streamwise coordinate of the pair position,
$x_{3}(s,x^{\infty }_{3})$ are defined by (C12) and (C13). The streamwise coordinate of the pair position, ![]() $\bar x_1$, does not affect the cross-flow particle distribution.
$\bar x_1$, does not affect the cross-flow particle distribution.
C.2.1. Trajectories on contact surface
The contact surface is defined by ![]() $s=s^*$, where
$s=s^*$, where ![]() $s^*=2$ for permeable particles and drops and
$s^*=2$ for permeable particles and drops and ![]() $s^*=2+\bar \delta$ for particles with surface roughness. In the compressional quadrant of the flow, the relative trajectory on the contact surface is described by setting the relative radial velocity to zero; particles separate in the extensional quadrant. The polar and azimuthal angles
$s^*=2+\bar \delta$ for particles with surface roughness. In the compressional quadrant of the flow, the relative trajectory on the contact surface is described by setting the relative radial velocity to zero; particles separate in the extensional quadrant. The polar and azimuthal angles ![]() $(\theta, \phi )$ evolve according to (C5) and (C6) over the range
$(\theta, \phi )$ evolve according to (C5) and (C6) over the range
where ![]() $(\theta _0, \phi _0)$ is the initial point of contact (point (ii) in figures 4 and 5); separation occurs at
$(\theta _0, \phi _0)$ is the initial point of contact (point (ii) in figures 4 and 5); separation occurs at ![]() $\phi ={\rm \pi} /2$ (point (iii)). Dividing the two equations and integrating yields (Rother & Davis Reference Rother and Davis2001)
$\phi ={\rm \pi} /2$ (point (iii)). Dividing the two equations and integrating yields (Rother & Davis Reference Rother and Davis2001)
 \begin{equation} \theta_1(\phi)=\tan^{{-}1}\left(\tan \theta_{0} \sqrt{\frac{1-B_{1}^{{\ast}}\cos(2\phi_{0})}{1-B_{1}^{{\ast}}\cos 2\phi}}\right), \end{equation}
\begin{equation} \theta_1(\phi)=\tan^{{-}1}\left(\tan \theta_{0} \sqrt{\frac{1-B_{1}^{{\ast}}\cos(2\phi_{0})}{1-B_{1}^{{\ast}}\cos 2\phi}}\right), \end{equation}
where ![]() $B_{1}^{\ast }=1-B(s^{\ast })$.
$B_{1}^{\ast }=1-B(s^{\ast })$.
The pair motion on the contact surface is obtained by dividing (C8) and (C9) by (C6) and integrating the range (C21) to yield,
and
where the functions ![]() $\varOmega (\phi )$ and
$\varOmega (\phi )$ and ![]() $\chi (\phi )$ are defined by
$\chi (\phi )$ are defined by
 \begin{equation} \varOmega(\phi)= \int_{\phi_0}^{\phi} \frac{[\hat r_{3}^2(\phi')-1] [ B_p^{{\ast}}\hat r_{1}(\phi') + 2(A_p'-B_p^{{\ast}})\hat r_{1}(\phi')\hat r_{2}^{2}(\phi')]}{\frac{1}{2}B^{{\ast}} [2\,\hat r_{2}^{2}(\phi')+\hat r_{3}^{2}(\phi')-1]-\hat r_{2}^{2}(\phi')}\,{\rm d} \phi', \end{equation}
\begin{equation} \varOmega(\phi)= \int_{\phi_0}^{\phi} \frac{[\hat r_{3}^2(\phi')-1] [ B_p^{{\ast}}\hat r_{1}(\phi') + 2(A_p'-B_p^{{\ast}})\hat r_{1}(\phi')\hat r_{2}^{2}(\phi')]}{\frac{1}{2}B^{{\ast}} [2\,\hat r_{2}^{2}(\phi')+\hat r_{3}^{2}(\phi')-1]-\hat r_{2}^{2}(\phi')}\,{\rm d} \phi', \end{equation}and
 \begin{equation} \chi(\phi)= \int_{\phi_0}^{\phi} \frac{ [\hat r_{3}^2(\phi')-1] [2 (A_p'-B_p^{{\ast}})\hat r_{1}(\phi')\hat r_{2}(\phi')\hat r_{3}(\phi')]}{\frac{1}{2}B^{{\ast}} [2 \hat r_{2}^{2}(\phi')+\hat r_{3}^{2}(\phi')-1]- \hat r_{2}^{2}(\phi')}\,{\rm d} \phi'. \end{equation}
\begin{equation} \chi(\phi)= \int_{\phi_0}^{\phi} \frac{ [\hat r_{3}^2(\phi')-1] [2 (A_p'-B_p^{{\ast}})\hat r_{1}(\phi')\hat r_{2}(\phi')\hat r_{3}(\phi')]}{\frac{1}{2}B^{{\ast}} [2 \hat r_{2}^{2}(\phi')+\hat r_{3}^{2}(\phi')-1]- \hat r_{2}^{2}(\phi')}\,{\rm d} \phi'. \end{equation}
Here, ![]() $\boldsymbol {\hat r}=(\hat r_{1},\hat r_{2},\hat r_{3})$ is the relative position vector on the contact surface
$\boldsymbol {\hat r}=(\hat r_{1},\hat r_{2},\hat r_{3})$ is the relative position vector on the contact surface
where ![]() $\theta _1(\phi )$ is given by (C22). The mobility functions
$\theta _1(\phi )$ is given by (C22). The mobility functions ![]() $B_p^{\ast }$ and
$B_p^{\ast }$ and ![]() $B^{\ast }$ in (C25) and (C26) are evaluated at
$B^{\ast }$ in (C25) and (C26) are evaluated at ![]() $s=s^{*}$, except that contact friction for rough particles, enters through a modified value of
$s=s^{*}$, except that contact friction for rough particles, enters through a modified value of ![]() $B^*$, as discussed in § C.4.
$B^*$, as discussed in § C.4.
The quantity ![]() $A_p'$ in (C25) and (C26) is the modified contact mobility that encompasses the correction resulting from the action of the contact force,
$A_p'$ in (C25) and (C26) is the modified contact mobility that encompasses the correction resulting from the action of the contact force, ![]() $F_c$. The latter quantity is required to prevent particle overlap and is determined by the force balance,
$F_c$. The latter quantity is required to prevent particle overlap and is determined by the force balance,
where ![]() $\mu$ is the continuous-phase viscosity, and
$\mu$ is the continuous-phase viscosity, and ![]() $G^{\ast }$ is the relative radial mobility function evaluated at contact. The contact force modifies the pair velocity for unequal size particles,
$G^{\ast }$ is the relative radial mobility function evaluated at contact. The contact force modifies the pair velocity for unequal size particles,
where ![]() $G_p^{\ast }$ is the pair radial mobility function evaluated at contact. Substituting the normal force derived from (C28) into (C29) yields
$G_p^{\ast }$ is the pair radial mobility function evaluated at contact. Substituting the normal force derived from (C28) into (C29) yields
where ![]() $A_p'=A_p^{\ast } + (1-A^{\ast }) G_p^{\ast }/G^{\ast }$ is the modified axisymmetric pair mobility that appears in formulas (C25) and (C26) (Zarraga & Leighton Reference Zarraga and Leighton2001). The modified mobility represents a higher-order correction, e.g. an
$A_p'=A_p^{\ast } + (1-A^{\ast }) G_p^{\ast }/G^{\ast }$ is the modified axisymmetric pair mobility that appears in formulas (C25) and (C26) (Zarraga & Leighton Reference Zarraga and Leighton2001). The modified mobility represents a higher-order correction, e.g. an ![]() $O(\bar \delta )$ correction for rough particles and an
$O(\bar \delta )$ correction for rough particles and an ![]() $O(K^{2/5})$ correction for permeable particles. There is no contact force for non-coalescing spherical drops because
$O(K^{2/5})$ correction for permeable particles. There is no contact force for non-coalescing spherical drops because ![]() $1-A^*=0$, according to the model described in § 4.1.3.
$1-A^*=0$, according to the model described in § 4.1.3.
C.3. Net cross-flow displacements
The indefinite trajectory integrals derived in § C.2 are combined here to yield formulas for the net relative and pair displacements in terms of the pair mobility functions. Relative and pair trajectory segments, (i–ii), (ii–iii) and (iii–iv) are defined in figure 4.
From (C12) and (C13), the relative cross-flow position at the contact point is
where ![]() $\varphi ^*$ and
$\varphi ^*$ and ![]() $\varPsi ^*$ are the functions (C15) and (C16) evaluated on the contact surface,
$\varPsi ^*$ are the functions (C15) and (C16) evaluated on the contact surface, ![]() $s=s^*$, and
$s=s^*$, and ![]() $\boldsymbol {x}^{({\rm i})}$ is the initial condition (C11a,b). The polar and azimuthal angles at the initial contact point
$\boldsymbol {x}^{({\rm i})}$ is the initial condition (C11a,b). The polar and azimuthal angles at the initial contact point ![]() $(\theta _0, \phi _0)$, are given by
$(\theta _0, \phi _0)$, are given by
The separation point is given by
where ![]() $\theta _1(x)$ is the function (C22). The final relative position of the particles in the cross-flow plane is
$\theta _1(x)$ is the function (C22). The final relative position of the particles in the cross-flow plane is
 \begin{equation} x^{({\rm iv})}_2=\left[\left(\frac{x_2^{({\rm iii})}}{\varphi^*}\right)^2 -\varPsi^*\right]^{1/2}, \quad x^{({\rm iv})}_3= \frac{x^{({\rm iii})}_3}{\varphi^*}. \end{equation}
\begin{equation} x^{({\rm iv})}_2=\left[\left(\frac{x_2^{({\rm iii})}}{\varphi^*}\right)^2 -\varPsi^*\right]^{1/2}, \quad x^{({\rm iv})}_3= \frac{x^{({\rm iii})}_3}{\varphi^*}. \end{equation}The displacement relations for the pair motion are obtained from (C17) and (C18) and (C23) and (C24), yielding the pair position
where ![]() $\bar \varphi ^*$ and
$\bar \varphi ^*$ and ![]() $\bar \varPsi ^*$ are the functions (C19) and (C20) evaluated at
$\bar \varPsi ^*$ are the functions (C19) and (C20) evaluated at ![]() $s=s^*$. The separation point is
$s=s^*$. The separation point is
where ![]() $\varOmega (x)$ and
$\varOmega (x)$ and ![]() $\chi (x)$ are the functions (C25) and (C26). The final cross-flow pair position is
$\chi (x)$ are the functions (C25) and (C26). The final cross-flow pair position is
The above results are combined to obtain the net relative and pair displacements
The net displacements of each particle, ![]() ${\rm \Delta} X^{12}_{k}$ and
${\rm \Delta} X^{12}_{k}$ and ![]() ${\rm \Delta} X^{21}_{k}$ (
${\rm \Delta} X^{21}_{k}$ (![]() $k=2,3$), are then obtained as
$k=2,3$), are then obtained as
Examples of particle displacements are shown in figures 6 and 7.
C.3.1. Collision cross-section
Combining (C34a,b) and using
yields the radius of the upstream collision cross-section,
 \begin{equation} \frac{r_c}{\bar a} =\left[\left(\frac{s^*}{\varphi^*}\right)^{2} -\varPsi^* \right]^{1/2}, \end{equation}
\begin{equation} \frac{r_c}{\bar a} =\left[\left(\frac{s^*}{\varphi^*}\right)^{2} -\varPsi^* \right]^{1/2}, \end{equation}
where ![]() $\varphi ^*$ and
$\varphi ^*$ and ![]() $\varPsi ^*$ are the mobility function integrals (C15) and (C16) evaluated on the contact surface,
$\varPsi ^*$ are the mobility function integrals (C15) and (C16) evaluated on the contact surface, ![]() $s=s^*$. Figures 8 and 9 show the radius of the collision cross-section for equal size particles.
$s=s^*$. Figures 8 and 9 show the radius of the collision cross-section for equal size particles.
C.4. Contact friction
Contact friction between rough particles affects only their relative motion on the contact surface, described by (C22) and enters through the transverse relative mobility function, ![]() $B^*$. Frictionless solid contact corresponds to
$B^*$. Frictionless solid contact corresponds to ![]() $B^*=B(s^*)$, where
$B^*=B(s^*)$, where ![]() $s^*=2+\bar \delta$. Finite contact friction increases the value of
$s^*=2+\bar \delta$. Finite contact friction increases the value of ![]() $B^*$. The limit of tangentially locking particle contacts is obtained using the contact value of the mobility function for smooth spheres, i.e.
$B^*$. The limit of tangentially locking particle contacts is obtained using the contact value of the mobility function for smooth spheres, i.e. ![]() $B^*=B(2)$. By increasing
$B^*=B(2)$. By increasing ![]() $B^*$, friction acts to move the polar angle between the particles from its incoming value,
$B^*$, friction acts to move the polar angle between the particles from its incoming value, ![]() $\theta _0$, towards
$\theta _0$, towards ![]() $\theta ={\rm \pi} /2$ according to (C22). At the point of separation,
$\theta ={\rm \pi} /2$ according to (C22). At the point of separation, ![]() $\phi ={\rm \pi} /2$, we have
$\phi ={\rm \pi} /2$, we have
under the assumption that ![]() $\phi _0<{\rm \pi} /2$. Thus, friction acts to increase relative particle displacements in the
$\phi _0<{\rm \pi} /2$. Thus, friction acts to increase relative particle displacements in the ![]() $X_2$-direction and diminish them in the
$X_2$-direction and diminish them in the ![]() $X_3$-direction, according to (C33a,b).
$X_3$-direction, according to (C33a,b).
C.4.1. Contacting permeable particles
The results in figure 5 of Reboucas & Loewenberg (Reference Reboucas and Loewenberg2022) show that the contact value of the transverse relative mobility for permeable particles, ![]() $B^*$, has the upper and lower bounds,
$B^*$, has the upper and lower bounds,
where ![]() $B(2)$ is the contact value of the hard-sphere mobility function, corresponding to rough particles with tangentially locking particle contacts; the equality holds for
$B(2)$ is the contact value of the hard-sphere mobility function, corresponding to rough particles with tangentially locking particle contacts; the equality holds for ![]() $\kappa =1$ because permeability has no effect on the transverse relative mobility for equal-size particles (Reboucas & Loewenberg Reference Reboucas and Loewenberg2022). The quantity
$\kappa =1$ because permeability has no effect on the transverse relative mobility for equal-size particles (Reboucas & Loewenberg Reference Reboucas and Loewenberg2022). The quantity ![]() $B(s^*_{eq})$ corresponds to frictionless contact between particles with equivalent roughness, where
$B(s^*_{eq})$ corresponds to frictionless contact between particles with equivalent roughness, where ![]() $s^*_{eq}=2+\bar \delta _{eq}$ with
$s^*_{eq}=2+\bar \delta _{eq}$ with ![]() $\bar \delta _{eq}$ defined by (4.1). Accordingly, particle displacements for permeable particles lie between the displacements for equivalent rough particles with frictionless and tangentially locking particle contacts.
$\bar \delta _{eq}$ defined by (4.1). Accordingly, particle displacements for permeable particles lie between the displacements for equivalent rough particles with frictionless and tangentially locking particle contacts.