Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T14:29:14.950Z Has data issue: false hasContentIssue false
  • English
  • Français

Parametrically forced stably stratified cavity flow: complicated nonlinear dynamics near the onset of instability

Published online by Cambridge University Press:  03 June 2019

Jason Yalim Open the ORCID record for Jason Yalim [Opens in a new window] ,
Bruno D. Welfert Open the ORCID record for Bruno D. Welfert [Opens in a new window]  and
Juan M. Lopez Open the ORCID record for Juan M. Lopez [Opens in a new window]
Jason Yalim
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe AZ 85287, USA
Bruno D. Welfert
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe AZ 85287, USA
Juan M. Lopez*
Affiliation:
School of Mathematical and Statistical Sciences, Arizona State University, Tempe AZ 85287, USA
*
†Email address for correspondence: juan.m.lopez@asu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of a fluid-filled square cavity with stable thermal stratification subjected to harmonic vertical oscillations is investigated numerically. The nonlinear responses to this parametric excitation are studied over a comprehensive range of forcing frequencies up to two and a half times the buoyancy frequency. The nonlinear results are in general agreement with the Floquet analysis, indicating the presence of nested resonance tongues corresponding to the intrinsic 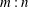$m:n$ eigenmodes of the stratified cavity. For the lowest-order subharmonic 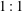$1:1$ tongue, the responses are analysed in great detail, with complex dynamics identified near onset, most of which involves interactions with unstable saddle states of a homoclinic or heteroclinic nature.

JFM classification

Instability: Parametric instability Geophysical and Geological Flows: Stratified flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 1067 - 1096
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abshagen, J., Lopez, J. M., Marques, F. & Pfister, G. 2005 Mode competition of rotating waves in reflection-symmetric Taylor–Couette flow. J. Fluid Mech. 540, 269–299.Google Scholar
Benielli, D. & Sommeria, J. 1998 Excitation and breaking of internal gravity waves by parametric instability. J. Fluid Mech. 374, 117–144.Google Scholar
Benjamin, T. B. & Ursell, F. 1954 The stability of the plane free surface of a liquid in vertical periodic motion. Proc. R. Soc. Lond. A 225, 505–515.Google Scholar
Bouruet-Aubertot, P., Sommeria, J. & Staquet, C. 1995 Breaking of standing internal gravity waves through two-dimensional instabilities. J. Fluid Mech. 285, 265–301.Google Scholar
Broer, H., Simó, C. & Vitolo, R. 2008 Hopf saddle-node bifurcation for fixed points of 3D-diffeomorphisms: analysis of a resonance bubble. Physica D 237, 1773–1799.Google Scholar
Dauxois, T., Joubaud, S., Odier, P. & Venaille, A. 2018 Instabilities of internal gravity wave beams. Annu. Rev. Fluid Mech. 50, 1–28.Google Scholar
Drazin, P. G. 1977 On the instability of an internal gravity wave. Proc. R. Soc. Lond. A 356, 411–432.Google Scholar
Fauve, S., Kumar, K., Laroche, C., Beysens, D. & Garrabos, Y. 1992 Parametric instability of a liquid–vapour interface close to the critical point. Phys. Rev. Lett. 68, 3160–3163.Google Scholar
Feigenbaum, M. J. 1978 Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 19, 25–52.Google Scholar
Gaspard, P. 1990 Measurement of the instability rate of a far-from-equilibrium steady state at an infinite period bifurcation. J. Phys. Chem. 94, 1–3.Google Scholar
Glendinning, P. 1984 Bifurcations near homoclinic orbits with symmetry. Phys. Lett. 103A, 163–166.Google Scholar
Kumar, K. & Tuckerman, L. S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.Google Scholar
Kuznetsov, Y. A. 2004 Elements of Applied Bifurcation Theory, 3rd edn. Springer.Google Scholar
Lopez, J. M. & Marques, F. 2000 Dynamics of 3-tori in a periodically forced Navier–Stokes flow. Phys. Rev. Lett. 85, 972–975.Google Scholar
Lopez, J. M., Marques, F. & Shen, J. 2004 Complex dynamics in a short annular cylinder with rotating bottom and inner cylinder. J. Fluid Mech. 501, 327–354.Google Scholar
Lopez, J. M., Welfert, B. D., Wu, K. & Yalim, J. 2017 Transition to complex dynamics in the cubic lid-driven cavity. Phys. Rev. Fluids 2, 074401.Google Scholar
Marques, F., Lopez, J. M. & Shen, J. 2001 A periodically forced flow displaying symmetry breaking via a three-tori gluing bifurcation and two-tori resonances. Physica D 156, 81–97.Google Scholar
May, R. M. 1976 Simple mathematical models with very complicated dynamics. Nature 261, 459–467.Google Scholar
McEwan, A. D. 1971 Degeneration of resonantly-excited standing internal gravity waves. J. Fluid Mech. 50, 431–448.Google Scholar
McEwan, A. D. 1983 The kinematics of stratified mixing through internal wavebreaking. J. Fluid Mech. 128, 47–57.Google Scholar
McEwan, A. D., Mander, D. W. & Smith, R. K. 1972 Forced resonant second-order interaction between damped internal waves. J. Fluid Mech. 55, 589–608.Google Scholar
McEwan, A. D. & Robinson, R. M. 1975 Parametric instability of internal gravity waves. J. Fluid Mech. 67, 667–687.Google Scholar
Mercader, I., Batiste, O. & Alonso, A. 2010 An efficient spectral code for incompressible flows in cylindrical geometries. Comput. Fluids 39, 215–224.Google Scholar
Miles, J. & Henderson, D. M. 1990 Parametrically forced surface-waves. Annu. Rev. Fluid Mech. 22, 143–165.Google Scholar
Oldeman, B. E., Krauskopf, B. & Champneys, A. R. 2000 Death of period-doublings: locating the homoclinic-doubling cascade. Physica D 146, 100–120.Google Scholar
Orlanski, I. 1972 On the breaking of standing internal gravity waves. J. Fluid Mech. 54, 577–598.Google Scholar
Orlanski, I. 1973 Trapeze instability as a source of internal gravity waves. Part I. J. Atmos. Sci. 30, 1007–1016.Google Scholar
Sherman, F. S., Imberger, J. & Corcos, G. M. 1978 Turbulence and mixing in stably stratified waters. Annu. Rev. Fluid Mech. 10, 267–288.Google Scholar
Smale, S. 1967 Differentiable dynamical systems. Bull. Am. Math. Soc. 73, 747–817.Google Scholar
Staquet, C. 2004 Gravity and inertia-gravity waves: breaking processes and induced mixing. Surv. Geophys. 25, 281–314.Google Scholar
Thorpe, S. A. 1968 On standing internal gravity waves of finite amplitude. J. Fluid Mech. 32, 489–528.Google Scholar
Thorpe, S. A. 1994 Observations of parametric instability and breaking waves in an oscillating tilted tube. J. Fluid Mech. 261, 33–45.Google Scholar
Wu, K., Welfert, B. D. & Lopez, J. M. 2018 Complex dynamics in a stratified lid-driven square cavity flow. J. Fluid Mech. 855, 43–66.Google Scholar
Yalim, J., Lopez, J. M. & Welfert, B. D. 2018 Vertically forced stably stratified cavity flow: instabilities of the basic state. J. Fluid Mech. 851, R6.Google Scholar
Yalim, J., Welfert, B., Lopez, J. & Wu, K. 2017a Fluid flow in a vertically oscillating, stably stratified cubic cavity. In 70th Annual Meeting of the APS Division of Fluid Dynamics, p. L34.010.Google Scholar
Yalim, J., Welfert, B., Lopez, J. & Wu, K. 2017b V0066: Resonant collapse in a harmonically forced stratified cavity. In 70th Annual Meeting of the APS Division of Fluid Dynamics, doi:10.1103/APS.DFD.2017.GFM.V0066.Google Scholar
Yih, C.-S. 1960 Gravity waves in a stratified fluid. J. Fluid Mech. 8, 481–508.Google Scholar

Yalim Supplementary Movie 1

Animation of the vorticity $\eta$ of three limit cycle states corresponding to figure 3 over one response period (two forcing periods). The three limit cycles are L$_{1:2}$ at forcing frequency $\omega=0.91$ with forcing amplitude $\alpha=0.16$, L$_{1:1}$ at $\omega=1.41$ with $\alpha=0.07$, and L$_{2:1}$ at $\omega=1.81$ with $\alpha=0.06$.

Download Yalim Supplementary Movie 1(Video)
Video 1.6 MB

Yalim Supplementary Movei 2

Animation corresponding to figure 14, illustrating how the local and global strobe maps of the flow at forcing frequency $\omega=1.35$ vary with forcing amplitude $\alpha$. Demonstrates the homoclinic doubling cascade as $\alpha$ is decreased.

Download Yalim Supplementary Movei 2(Video)
Video 13.1 MB

Yalim Supplementary Movie 3

Animation of the isotherms $T$ (first row) and vorticity $\eta$ (second row) of the four indicated limit cycles over two forcing periods at forcing frequency $\omega=1.41$. The limit cycles shown are L$_{1:1}$ at forcing amplitude $\alpha=0.07$ (first column), L$_L$ at $\alpha=0.105$ (second column), L$_R$ at $\alpha=0.105$ (third column), and L$_{2:2}$ at $\alpha=0.105$ (fourth column). Corresponds to figure 15.

Download Yalim Supplementary Movie 3(Video)
Video 2.6 MB

Yalim Supplementary Movie 4

Animation of the isotherms $T$ (left column) and vorticity $\eta$ (rightcolumn) for the S$_2$ state at $(\omega,\alpha)=(1.41,0.111)$ over sixforcing periods. Obtained by restricting the direct numerical simulationto the $\Kz$ symmetry subspace. Corresponds to figure 16.

Download Yalim Supplementary Movie 4(Video)
Video 7.4 MB

Yalim Supplementary Movie 5

Animation summarizing the dynamics observed in the $\Rpi$ symmetry subspace as an indicated forcing amplitude $\alpha$ is increased by $0.01$ for fixed forcing frequency $\omega=1.41$, with the variance of a horizontal velocity at a point $\varSigma$ (first row, first column), the number of forcing periods $\omega/\omega_R$ associated with the slow response of the 2-tori states (second row, first column), and the associated strobe map sampling a horizontal velocity at a point $u_p$ and a global measure of the temperature $\ET$ every two forcing periods at forcing phase $\pi$ (second column). Corresponds to figure 18.

Download Yalim Supplementary Movie 5(Video)
Video 1.2 MB

Yalim Supplementary Movie 6

Animation of the strobe maps of a horizontal velocity at a point with a global measure of the temperature $(u_p,\ET)$ and strobed vorticity $\eta$ of Q$_L$, Q$_R$, and Q at fixed forcing frequency $\omega=1.41$ and indicated forcing amplitude $\alpha$ near the first gluing. Q$_L$ and Q$_R$ are shown at $\alpha=0.125$, and Q is shown at $\alpha=0.126$. The strobe is taken every two forcing periods at forcing phase $\pi$. Corresponds to figure 20.

Download Yalim Supplementary Movie 6(Video)
Video 10.8 MB

Yalim Supplementary Movie 7

Animation of the strobe maps of a horizontal velocity at a point with a global measure of the temperature $(u_p,\ET)$ and strobed vorticity $\eta$ of Q$_L$, Q$_R$, and Q at fixed forcing frequency $\omega=1.41$ and indicated forcing amplitude $\alpha$ near the first gluing. Q$_L$ and Q$_R$ are shown at $\alpha=0.125$, and Q is shown at $\alpha=0.126$. The strobe is taken every two forcing periods at forcing phase $\pi$. Corresponds to figure 20.

Download Yalim Supplementary Movie 7(Video)
Video 11.6 MB

Yalim Supplementary Movie 8

Animation summarizing the upper-branch dynamics observed in the fullspace as an indicated forcing amplitude $\alpha$ is increased by $0.01$ for fixed forcing frequency $\omega=1.41$, with the variance of a horizontal velocity at a point $\varSigma_u$ (first row, first column), the number of forcing periods $\omega/\omega_R$ associated with the slow response of the 2-tori and 3-tori states (second row, first column), and the associated strobe map sampling a horizontal velocity at a point $u_p$ and a global measure of the temperature $\ET$ every two forcing periods at forcing phase $\pi$ (second column). Corresponds to figure 24.

Download Yalim Supplementary Movie 8(Video)
Video 4.2 MB

Yalim Supplementary Movie 9

Animation comparing strobed full space dynamics of Q$_R$ (left column) and T$_{3R}$ (right column) at forcing frequency $\omega=1.41$ and forcing amplitude $\alpha=0.138$ with a two forcing period strobe map of a horizontal velocity at point and a global measure of the temperature $(u_p,\ET)$ at forcing phase $\pi$ (first row) and the strobed vorticity $\eta$ (second row). Corresponds to figure 25.

Download Yalim Supplementary Movie 9(Video)
Video 4.9 MB