Article contents
Passive bionic motion of a flexible film in the wake of a circular cylinder: chaos and periodicity, flow–structure interactions and energy evolution
Published online by Cambridge University Press: 10 May 2024
Abstract
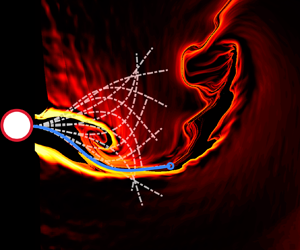
The self-sustained interactions between a flexible film and periodic vortices epitomize the spirit of fish swimming and flag flapping in nature, involving intricate patterns of flow–structure coupling. Here, we comprehensively investigate the multiple coupling states of a film in the cylinder wake mainly with experiments, complemented by theoretical solutions and nonlinear dynamical analyses. Four regimes of film motion states are identified in the parameter space spanned by the reduced velocity and the length ratio. These regimes are (i) keeping stationary, (ii) deflection flutter, (iii) hybrid flutter and (iv) periodic large-amplitude flapping, each governed by a distinct coupling mechanism, involving regular and irregular Kármán vortices, local instability of the elongated shear layers and 2P mode vortex shedding. The film futtering in regimes (ii) and (iii) is substantiated to be chaotic and bears a resemblance to the ‘entraining state’ of fish behind an obstacle in the river. The periodic flapping in regime (iv) manifests itself in an amalgam of standing and travelling waves, and has intrinsic relations to the ‘Kármán gaiting’ of fish in periodic vortices. With the spatiotemporal reconstruction for the periodic flapping, we procure the energy distributions on the film, revealing the energy transfer processes between the film and the large-scale vortices. The findings unequivocally indicate that the flow–structure interaction during the energy-release stage of the film is more intense than that during the energy-extraction stage. Given the similarities, the mathematical and physical methods presented in this work are also applicable to the research on biological undulatory locomotion.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Duan and Wang supplementary movie 1
Duan and Wang supplementary movie 2
Duan and Wang supplementary movie 3
Duan and Wang supplementary movie 4
- 8
- Cited by


