Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T06:33:24.919Z Has data issue: false hasContentIssue false
  • English
  • Français

Path instabilities of oblate spheroids

Published online by Cambridge University Press:  06 November 2017

W. Zhou ,
M. Chrust  and
J. Dušek Open the ORCID record for J. Dušek [Opens in a new window]
W. Zhou
Affiliation:
ICube, Department of Fluid Mechanics, Université de Strasbourg/CNRS, 2, rue Boussingault, 67000 Strasbourg, France
M. Chrust
Affiliation:
Earth System Assimilation Section, Data Assimilation Methodology Group, European Centre for Medium-Range Weather Forecasts Shinfield Park, Reading RG2 9AX, UK
J. Dušek*
Affiliation:
ICube, Department of Fluid Mechanics, Université de Strasbourg/CNRS, 2, rue Boussingault, 67000 Strasbourg, France
*
†Email address for correspondence: dusek@unistra.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In the present paper, we investigate the path instabilities and the transition scenario for oblate homogeneous spheroids falling (or ascending) freely in a quiescent and unconfined Newtonian fluid under the action of gravity, buoyancy and hydrodynamic forces. The problem depends on three independent external parameters: the aspect ratio 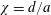$\unicode[STIX]{x1D712}=d/a$ , where 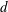$d$ is the diameter and $a$ the length of the axisymmetry axis of the spheroid; the non-dimensionalized mass 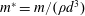$m^{\ast }=m/(\unicode[STIX]{x1D70C}d^{3})$ , 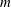$m$ being the mass of the spheroid and 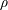$\unicode[STIX]{x1D70C}$ the fluid density; and the Galileo number, defined as 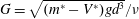$G=\sqrt{(m^{\ast }-V^{\ast })gd^{3}}/\unicode[STIX]{x1D708}$ . In the definition of the Galileo number, 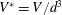$V^{\ast }=V/d^{3}$ is the non-dimensionalized volume, 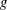$g$ the gravitational acceleration and $\unicode[STIX]{x1D708}$ is the kinematic viscosity. Asymptotic solutions (regimes) are investigated in seven 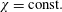$\unicode[STIX]{x1D712}=\text{const}.$ parameter planes going from 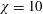$\unicode[STIX]{x1D712}=10$ (very flat spheroid) to 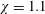$\unicode[STIX]{x1D712}=1.1$ (an almost spherical shape), for 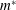$m^{\ast }$ going from 0 to 5 and Galileo numbers up to 300 (i.e. Reynolds numbers roughly up to 500). The obtained results provide a link between the known scenario of a homogeneous disk and that, well known, of a sphere. The scenario of the flat spheroid of aspect ratio 10 has many common features with that of an infinitely thin disk, but the finite thickness brings about significant quantitative differences. At the opposite side of the investigated aspect ratio interval, the dynamics of the spheroid of aspect ratio 1.1 is found very close to that of a perfect sphere except for small density ratios (smaller than approximately 0.5). Very light spheroids of aspect ratio 1.1 move along vertical zig-zagging trajectories. At intermediate aspect ratios, the strong subcritical effects and the characteristic zig-zagging and fluttering motion, typical for flat bodies, progressively disappear. The tumbling regime remains remarkably stable and is shown to be present down to 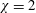$\unicode[STIX]{x1D712}=2$ . An interesting result consists in the evidence of the first two bifurcations typical for the sphere scenario (leading to steady oblique and oblique oscillating trajectories) present both for very flat and thick spheroids but absent at intermediate aspect ratios. The results pertaining to spheroids might be more useful in practical applications than those obtained for too idealized thin disks and perfect spheres.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Multiphase and Particle-laden Flows: Particle/fluid flow Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 833 , 25 December 2017 , pp. 445 - 468
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auguste, F.2010 Instabilités de sillage générées derrière un corps solide cylindrique, fixe ou mobile dans un fluide visqueux. PhD thesis, Université Paul Sabatier, Toulouse.Google Scholar
Auguste, F., Magnaudet, J. & Fabre, D. 2013 Falling styles of discs. J. Fluid Mech. 719, 388–405.Google Scholar
Chrust, M.2012 Etude numérique de la chute d’objets axisymétriques dans un fluide newtonien. PhD thesis, Université de Strasbourg.Google Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2010 Parametric study of the transition in the wake of oblate spheroids and flat cylinders. J. Fluid Mech. 665, 199–208.CrossRefGoogle Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2013 Numerical simulation of the dynamics of freely falling discs. Phys. Fluids 25, 044102.Google Scholar
Chrust, M., Bouchet, G. & Dušek, J. 2014 Effect of solid body degrees of freedom on the path instabilities of freely falling or rising flat cylinders. J. Fluids Struct. 47, 55–70.CrossRefGoogle Scholar
Ern, P., Risso, F., Fabre, D. & Magnaudet, J. 2011 Wake-induced oscillatory paths of bodies freely rising of falling in fluids. Annu. Rev. Fluid Mech. 44, 97–121.CrossRefGoogle Scholar
Fabre, D., Auguste, F. & Magnaudet, J. 2008 Bifurcations and symmetry breaking in the wake of axisymmetric bodies. Phys. Fluids 20, 051702.CrossRefGoogle Scholar
Fabre, D., Tchoufag, J. & Magnaudet, J. 2012 The steady oblique path of bouyancy-driven disks and spheres. J. Fluid Mech. 707, 24–36.Google Scholar
Fernandes, P. C., Risso, F., Ern, P. & Magnaudet, J. 2007 Oscillatory motion and wake instability of freely rising axisymmetric bodies. J. Fluid Mech. 573, 479–502.Google Scholar
Field, S. B., Klaus, M. & Moore, M. G. 1997 Chaotic dynamics of falling disks. Nature 388, 252–254.Google Scholar
Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.Google Scholar
Jenny, M. & Dušek, J. 2004 Efficient numerical method for the direct numerical simulation of the flow past a single light moving spherical body in transitional regimes. J. Comput. Phys. 194, 215–232.Google Scholar
Jenny, M., Dušek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.Google Scholar
Stringham, G. E., Simons, D. B. & Guy, H. P. 1969 The Behavior of Large Particles Falling in Quiescent Liquids. U.S. Government Printing Office.Google Scholar
Tchoufag, J., Fabre, D. & Magnaudet, J. 2014 Global linear stability analysis of the wake and path of buoyancy-driven disks and thin cylinders. J. Fluid Mech. 740, 278–311.Google Scholar
Uhlmann, M. & Doychev, T. 2014 Sedimentation of a dilute suspension of rigid spheres at intermediate Galileo numbers: the effect of clustering upon the particle motion. J. Fluid Mech. 752, 310–348.Google Scholar
Uhlmann, M. & Dušek, J. 2014 The motion of a single heavy sphere in ambient fluid: a benchmark for interface-resolved particulate flow simulations with significant relative velocities. Intl J. Multiphase Flow 59, 221–243.CrossRefGoogle Scholar
Willmarth, W. W., Hawk, N. E. & Harvey, R. L. 1964 Steady and unsteady motions and wakes of freely falling disks. Phys. Fluids 7, 197–208.Google Scholar
Zhong, H., Chen, S. & Lee, C. 2011 Experimental study of freely falling thin disks: Transition from planar zigzag to spiral. Phys. Fluids 23 (1), 011702.Google Scholar
Zhou, W. & Dušek, J. 2015 Chaotic states and order in the chaos of the paths of freely falling and ascending spheres. Intl J. Multiphase Flow 75, 205–223.CrossRefGoogle Scholar