Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Muscutt, Luke E.
Dyke, Gareth
Weymouth, Gabriel D.
Naish, Darren
Palmer, Colin
and
Ganapathisubramani, Bharathram
2017.
The four-flipper swimming method of plesiosaurs enabled efficient and effective locomotion.
Proceedings of the Royal Society B: Biological Sciences,
Vol. 284,
Issue. 1861,
p.
20170951.
Leung, Jordan M.
Wong, Jaime G.
Weymouth, Gabriel D.
and
Rival, David E.
2018.
Modeling Transverse Gusts Using Pitching, Plunging, and Surging Airfoil Motions.
AIAA Journal,
Vol. 56,
Issue. 8,
p.
3271.
Kurt, Melike
and
Moored, Keith
2018.
Unsteady Performance of Finite-Span Pitching Propulsors in Side-by-Side Arrangements.
Kurt, Melike
and
Moored, Keith W
2018.
Flow interactions of two- and three-dimensional networked bio-inspired control elements in an in-line arrangement.
Bioinspiration & Biomimetics,
Vol. 13,
Issue. 4,
p.
045002.
Zhao, Zhijie
and
Dou, Lei
2019.
Effects of the structural relationships between the fish body and caudal fin on the propulsive performance of fish.
Ocean Engineering,
Vol. 186,
Issue. ,
p.
106117.
Moriche, Manuel
Gonzalo, Alejandro
Flores, Oscar
and
Garcia-Villalba, Manuel
2019.
Fast transverse maneuvers at low Reynolds numbers.
Shanmugam, A. R.
and
Sohn, C. H.
2019.
Numerical investigation on thrust production and unsteady mechanisms of three-dimensional oscillating wing.
Journal of Mechanical Science and Technology,
Vol. 33,
Issue. 12,
p.
5889.
Brooks, Seth A.
and
Green, Melissa A.
2019.
Experimental Study of Body-Fin Interaction and Vortex Dynamics Generated by a Two Degree-Of-Freedom Fish Model.
Biomimetics,
Vol. 4,
Issue. 4,
p.
67.
Viswanath, Kamal
Sharma, Alisha
Gabbita, Saketh
Geder, Jason
Ramamurti, Ravi
and
Pruessner, Marius
2019.
Evaluation of Surrogate Models for Multi-fin Flapping Propulsion Systems.
p.
1.
Lin, Xingjian
Wu, Jie
Zhang, Tongwei
and
Yang, Liming
2019.
Phase difference effect on collective locomotion of two tandem autopropelled flapping foils.
Physical Review Fluids,
Vol. 4,
Issue. 5,
Ortega-Casanova, Joaquin
and
Fernandez-Feria, Ramon
2019.
Maximum propulsive efficiency of two pitching and plunging plates in tandem at low Reynolds number.
International Journal of Numerical Methods for Heat & Fluid Flow,
Vol. 29,
Issue. 11,
p.
4013.
Alaminos-Quesada, Javier
and
Fernandez-Feria, Ramón
2020.
Aerodynamics of Heaving and Pitching Foils in Tandem from Linear Potential Theory.
AIAA Journal,
Vol. 58,
Issue. 1,
p.
37.
Lagopoulos, N. S.
Weymouth, G. D.
and
Ganapathisubramani, B.
2020.
Deflected wake interaction of tandem flapping foils.
Journal of Fluid Mechanics,
Vol. 903,
Issue. ,
Lin, Xingjian
Wu, Jie
Zhang, Tongwei
and
Yang, Liming
2020.
Self-organization of multiple self-propelling flapping foils: energy saving and increased speed.
Journal of Fluid Mechanics,
Vol. 884,
Issue. ,
Wu, Xia
Zhang, Xiantao
Tian, Xinliang
Li, Xin
and
Lu, Wenyue
2020.
A review on fluid dynamics of flapping foils.
Ocean Engineering,
Vol. 195,
Issue. ,
p.
106712.
Şimşek, Emre
Freeman, Benjamin
Şentürk, Utku
and
Hemmati, Arman
2020.
Effect of In-Line Tandem Configuration on Performance and Scaling of Pitching Hydrofoils.
AIAA Journal,
Vol. 58,
Issue. 11,
p.
4620.
Moriche, M
Raiola, M
Discetti, S
Ianiro, A
Flores, O
and
García-Villalba, M
2020.
Assessing aerodynamic force estimation with experiments and simulations of flapping-airfoil flows on the verge of three-dimensionality.
Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering,
Vol. 234,
Issue. 2,
p.
428.
Kurt, Melike
Eslam Panah, Azar
and
Moored, Keith W.
2020.
Flow Interactions Between Low Aspect Ratio Hydrofoils in In-line and Staggered Arrangements.
Biomimetics,
Vol. 5,
Issue. 2,
p.
13.
Arranz, G.
Flores, O.
and
García-Villalba, M.
2020.
Direct and Large Eddy Simulation XII.
Vol. 27,
Issue. ,
p.
297.
Zurman-Nasution, A. N.
Ganapathisubramani, B.
and
Weymouth, G. D.
2020.
Influence of three-dimensionality on propulsive flapping.
Journal of Fluid Mechanics,
Vol. 886,
Issue. ,
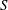 $S$ ) and phasing (
$S$ ) and phasing ( 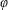 $\unicode[STIX]{x1D711}$ ) to be investigated over a range of non-dimensional frequencies (or Strouhal number,
$\unicode[STIX]{x1D711}$ ) to be investigated over a range of non-dimensional frequencies (or Strouhal number, 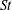 $St$ ). Results indicate that the hind foil can produce from no thrust to twice the thrust of a single foil depending on its spacing and phasing with respect to the fore foil, which is consistent with previous studies that were carried out over a limited parameter space. Examination of instantaneous flow fields indicates that high thrust occurs when the hind foil weaves between the vortices that have been shed by the fore foil, and low thrust occurs when the hind foil intercepts these vortices. Contours of high thrust and minimal thrust appear as inclined bands in the
$St$ ). Results indicate that the hind foil can produce from no thrust to twice the thrust of a single foil depending on its spacing and phasing with respect to the fore foil, which is consistent with previous studies that were carried out over a limited parameter space. Examination of instantaneous flow fields indicates that high thrust occurs when the hind foil weaves between the vortices that have been shed by the fore foil, and low thrust occurs when the hind foil intercepts these vortices. Contours of high thrust and minimal thrust appear as inclined bands in the 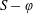 $S-\unicode[STIX]{x1D711}$ parameter space and this behaviour is apparent over the entire range of Strouhal numbers considered
$S-\unicode[STIX]{x1D711}$ parameter space and this behaviour is apparent over the entire range of Strouhal numbers considered 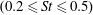 $(0.2\leqslant St\leqslant 0.5)$ . A novel quasi-steady model that utilises kinematics of a virtual hind foil together with data obtained from simulations of a single flapping foil shows that performance augmentation is primarily determined through modification of the instantaneous angle of attack of the hind foil by the vortex street established by the fore foil. This simple model provides estimates of thrust and efficiency for the hind foil, which is consistent with data obtained through full simulations. The limitations of the virtual hind foil method and its physical significance is also discussed.
$(0.2\leqslant St\leqslant 0.5)$ . A novel quasi-steady model that utilises kinematics of a virtual hind foil together with data obtained from simulations of a single flapping foil shows that performance augmentation is primarily determined through modification of the instantaneous angle of attack of the hind foil by the vortex street established by the fore foil. This simple model provides estimates of thrust and efficiency for the hind foil, which is consistent with data obtained through full simulations. The limitations of the virtual hind foil method and its physical significance is also discussed.