Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-29T13:01:17.042Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbing vortex packets in a turbulent boundary layer

Published online by Cambridge University Press:  29 April 2014

Shaokai Zheng  and
Ellen K. Longmire
Shaokai Zheng
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Ellen K. Longmire*
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
*
†Email address for correspondence: longmire@umn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A zero pressure gradient turbulent boundary layer of 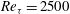$\textit {Re}_{\tau }=2500$ was perturbed by a single spanwise array of finite cylinders mounted on the bounding surface and extending through the logarithmic region. The cylinder height was 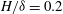$H/\delta =0.2$ (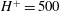$H^{+}=500$), where 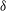$\delta $ is the boundary layer thickness, with an aspect ratio (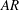$AR$) (height/diameter) of four. Streamwise–spanwise (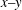$x\text {--}y$) planes of the flow were examined by particle image velocimetry (PIV) up to 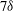$7\delta $ downstream at a wall-normal location of 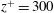$z^{+}=300$ for cylinder array spacings ranging from 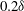$0.2\delta $ to 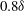$0.8\delta $. Average streamwise velocity fields showed a splitting, then merging pattern of cylinder wakes which occurred further downstream as the cylinder spacing increased. Based on measurements at the furthest downstream location, both the spanwise variation of average streamwise velocity and the Fourier content in the instantaneous fields suggested that the case with 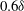$0.6\delta $ cylinder spacing, which matched the dominant spanwise scale in the unperturbed flow, yielded the most persistent downstream flow organization. A flying PIV method was implemented to track specific packet structures over a range 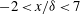$-2<x/\delta <7$ with respect to the cylinder array, corresponding to a time scale of 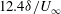$12.4\delta /U_{\infty }$. Packets approaching the 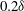$0.2\delta $ spacing array first lost their organization but then regained it a distance 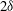$2\delta $ downstream, suggesting that a persistent outer layer organization propagated inwards into the log region. For arrays with larger spanwise spacing, approaching packets were generally redirected into the spanwise location midway between cylinders and sometimes enhanced.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulence control
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 368 - 398
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adrian, R. J. 2007 Hairpin vortex organization in wall turbulence. Phys. Fluids 19 (4), 041301.Google Scholar
Adrian, R. J. & Liu, Z. C. 2002 Observation of vortex packets in direct numerical simulation of fully turbulent channel flow. J. Visual.-Japan 5 (1), 9–19.Google Scholar
Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Atkinson, C., Chumakov, S., Bermejo-Moreno, I. & Soria, J. 2012 Lagrangian evolution of the invariants of the velocity gradient tensor in a turbulent boundary layer. Phys. Fluids 24 (10), 1–14.Google Scholar
Belcher, S. E., Jerram, N. & Hunt, J. C. R. 2003 Adjustment of a turbulent boundary layer to a canopy of roughness elements. J. Fluid Mech. 488, 369–398.Google Scholar
Castro, I. P., Cheng, H. & Reynolds, R. 2006 Turbulence over urban-type roughness: deductions from wind-tunnel measurements. Boundary-Layer Meteorol. 118 (1), 109–131.Google Scholar
Christensen, K. T. & Adrian, R. J. 2001 Statistical evidence of hairpin vortex packets in wall turbulence. J. Fluid Mech. 431, 433–443.CrossRefGoogle Scholar
Coceal, O., Dobre, A., Thomas, T. G. & Belcher, S. E. 2007 Structure of turbulent flow over regular arrays of cubical roughness. J. Fluid Mech. 589, 375–409.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011a Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 1. Vortex packets. J. Fluid Mech. 673, 180–217.Google Scholar
Dennis, D. J. C. & Nickels, T. B. 2011b Experimental measurement of large-scale three-dimensional structures in a turbulent boundary layer. Part 2. Long structures. J. Fluid Mech. 673, 218–244.Google Scholar
Dillon-Gibbons, C. J., Wong, C. Y., Chen, L. & Soria, J.2007 Cylinder wake - boundary layer interaction in the near field. In Proceedings of 16th Australasian Fluid Mechanics Conference, Gold Coast, Australia (ed. P. Jacobs, P. McIntyre, M. Cleary, D. Buttsworth, D. Mee, C. Rose, R. Morgan & C. Lemckert), pp. 1475–1480. School of Engineering, The University of Queensland.Google Scholar
Elsinga, G. E., Adrian, R. J., van Oudheusden, B. W. & Scarano, F. 2010 Three-dimensional vortex organization in a high-Reynolds-number supersonic turbulent boundary layer. J. Fluid Mech. 644, 35–60.Google Scholar
Elsinga, G. E., Kuik, D. J., van Oudheusden, B. W. & Scarano, F.2007 Investigation of the three-dimensional coherent structures in a turbulent boundary layer with tomographic-PIV. In Proceedings of 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, AIAA.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Evolution and lifetimes of flow topology in a turbulent boundary layer. Phys. Fluids 22 (1), 1–9.CrossRefGoogle Scholar
Elsinga, G. E., Poelma, C., Schröder, A., Geisler, R., Scarano, F. & Westerweel, J. 2012 Tracking of vortices in a turbulent boundary layer. J. Fluid Mech. 697, 273–295.Google Scholar
Ganapathisubramani, B., Hutchins, N., Hambleton, W. T., Longmire, E. K. & Marusic, I. 2005 Investigation of large-scale coherence in a turbulent boundary layer using two-point correlations. J. Fluid Mech. 524, 57–80.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2003 Characteristics of vortex packets in turbulent boundary layers. J. Fluid Mech. 478, 35–46.Google Scholar
Ganapathisubramani, B., Longmire, E. K. & Marusic, I. 2006 Experimental investigation of vortex properties in a turbulent boundary layer. Phys. Fluids 18 (5), 1–14.Google Scholar
Gao, Q.2011 Evolution of eddies and packets in turbulent boundary layers. PhD thesis, University of Minnesota Twin Cities.Google Scholar
Gao, Q., Ortiz-Dueñas, C. & Longmire, E. K. 2013 Evolution of coherent structures in turbulent boundary layers based on moving tomographic PIV. Exp. Fluids 54 (12), 1–16.Google Scholar
Guala, M., Tomkins, C. D., Christensen, K. T. & Adrian, R. J. 2012 Vortex organization in a turbulent boundary layer overlying sparse roughness elements. J. Hydraul Res. 50 (5), 465–481.Google Scholar
Hain, R., Kähler, C. J. & Michaelis, D. 2008 Tomographic and time resolved PIV measurements on a finite cylinder mounted on a flat plate. Exp. Fluids 45, 715–724.Google Scholar
Hutchins, N., Ganapathisubramani, B. & Marusic, I.2005b Spanwise periodicity and the existence of very large scale coherence in turbulent boundary layers. In Proceedings of Turbulence and Shear Flow Phenomena IV, Williamsburg, VA, USA. TSFP.Google Scholar
Hutchins, N., Hambleton, W. T. & Marusic, I. 2005a Inclined cross-stream stereo particle image velocimetry measurements in turbulent boundary layers. J. Fluid Mech. 541, 21–54.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.Google Scholar
Ikeda, T. & Durbin, P. A. 2007 Direct simulations of a rough-wall channel flow. J. Fluid Mech. 571, 235–263.Google Scholar
Jacobi, I. & McKeon, B. J. 2011 New perspectives on the impulsive roughness-perturbation of a turbulent boundary layer. J. Fluid Mech. 677, 179–203.Google Scholar
Jiménez, J. 2004 Turbulent flows over rough walls. Annu. Rev. Fluid Mech. 36 (1), 173–196.Google Scholar
Lee, J. H. & Sung, H. J. 2011 Very-large-scale motions in a turbulent boundary layer. J. Fluid Mech. 673, 80–120.Google Scholar
LeHew, J. A., Guala, M. & McKeon, B. J. 2013 Time-resolved measurements of coherent structures in the turbulent boundary layer. Exp. Fluids 54 (4), 1–16.Google Scholar
Longmire, E. K., Gao, Q., Ryan, M. D. & Ortiz-Dueñas, C.2011 Examination of turbulent boundary layers by volumetric velocimetry. In Proceedings of 9th International Symposium on Particle Image Velocimetry, Kobe, Japan. International Symposium on Particle Image Velocimetry.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009 Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.Google Scholar
Orlandi, P., Leonardi, S. & Antonia, R. A. 2006 Turbulent channel flow with either transverse or longitudinal roughness elements on one wall. J. Fluid Mech. 561, 279–305.Google Scholar
Ortiz-Dueñas, C., Ryan, M. D. & Longmire, E. K.2011 Modification of turbulent boundary layer structure using immersed wall-mounted cylinders. In Proceedings of Turbulence and Shear Flow Phenomena VII, Ottawa, Canada. TSFP.CrossRefGoogle Scholar
Park, C. W. & Lee, S. J. 2002 Flow structure around a finite circular cylinder embedded in various atmospheric boundary layers. Fluid Dyn. Res. 30 (4), 197–215.Google Scholar
Park, C. W. & Lee, S. J. 2003 Flow structure around two finite circular cylinders located in an atmospheric boundary layer: side-by-side arrangement. J. Fluids Struct. 17 (8), 1043–1058.Google Scholar
Pujals, G., Cossu, C. & Depardon, S. 2010 Forcing large-scale coherent streaks in a zero-pressure-gradient turbulent boundary layer. J. Turbul. 11 (25), 1–13.Google Scholar
Ryan, M. D.2011 Planar and volumetric measurements downstream of cylinders immersed in a turbulent boundary layer. Master’s thesis, University of Minnesota Twin Cities.Google Scholar
Ryan, M. D., Ortiz-Dueñas, C. & Longmire, E. K. 2011 Effects of simple wall-mounted cylinder arrangements on a turbulent boundary layer. AIAA J. 49 (10), 2210–2220.Google Scholar
Sakamoto, H. & Arie, M. 1983 Vortex shedding from a rectangular prism and a circular-cylinder placed vertically in a turbulent boundary-layer. J. Fluid Mech. 126, 147–165.Google Scholar
Schofield, W. H. & Logan, E.1988 Viscous flow around two and three-dimensional wall mounted obstacles. In Proceedings of 1st AIAA, ASME, SIAM, and APS, National Fluid Dynamics Congress, Cincinnati, OH, USA, pp. 1742–1748. AIAA.Google Scholar
Simpson, R. L. 2001 Junction flows. Annu. Rev. Fluid Mech. 33, 415–443.Google Scholar
Sumner, D., Heseltine, J. L. & Dansereau, O. J. P. 2004 Wake structure of a finite circular cylinder of small aspect ratio. Exp. Fluids 37 (5), 720–730.Google Scholar
Tomkins, C. D.2001 The structure of turbulence over smooth and rough walls. PhD thesis, University of Illinois at Urbana–Champaign.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Wang, H. F., Zhou, Y., Chan, C. & Lam, K. 2006 Effect of initial conditions on interaction between a boundary layer and a wall-mounted finite-length-cylinder wake. Phys. Fluids 18 (6), 1–12.Google Scholar
Wark, C. E., Naguib, A. M. & Nagib, H. M. 1990 Effect of plate manipulators on coherent structures in a turbulent boundary-layer. AIAA J. 28 (11), 1877–1884.Google Scholar
Wark, C. E., Naguib, A. M. & Robinson, S. K.1991 Scaling of spanwise length scales in a turbulent boundary layer. In Proceedings of 29th AIAA Aerospace Sciences Meeting, Reno, NV, USA. AIAA.Google Scholar
Westerweel, J. 1994 Efficient detection of spurious vectors in particle image velocimetry data. Exp. Fluids 16, 236–247.CrossRefGoogle Scholar
Westerweel, J., Dabiri, D. & Gharib, M. 1997 The effect of a discrete window offset on the accuracy of cross-correlation analysis of digital PIV recordings. Exp. Fluids 23 (1), 20–28.Google Scholar
Wieneke, B. 2005 Stereo-PIV using self-calibration on particle images. Exp. Fluids 39, 267–280.Google Scholar
Williamson, C. H. K. 1996 Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.Google Scholar
Wu, Y. & Christensen, K. T. 2010 Spatial structure of a turbulent boundary layer with irregular surface roughness. J. Fluid Mech. 655, 380–418.Google Scholar
Zheng, S.2013 Perturbing spanwise modes in turbulent boundary layers. Master’s thesis, University of Minnesota Twin Cities.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar