Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T10:51:58.619Z Has data issue: false hasContentIssue false
  • English
  • Français

A physical conjecture for the dipolar–multipolar dynamo transition

Published online by Cambridge University Press:  15 July 2019

B. R. McDermott Open the ORCID record for B. R. McDermott [Opens in a new window]  and
P. A. Davidson Open the ORCID record for P. A. Davidson [Opens in a new window]
B. R. McDermott
Affiliation:
Department of Engineering, Cambridge University, CambridgeCB2 1PZ, UK
P. A. Davidson*
Affiliation:
Department of Engineering, Cambridge University, CambridgeCB2 1PZ, UK
*
†Email address for correspondence: pad3@eng.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

In numerical simulations of planetary dynamos there is an abrupt transition in the dynamics of both the velocity and magnetic fields at a ‘local’ Rossby number of 0.1. For smaller Rossby numbers there are helical columnar structures aligned with the rotation axis, which efficiently maintain a dipolar field. However, when the thermal forcing is increased, these columns break down and the field becomes multi-polar. Similarly, in rotating turbulence experiments and simulations there is a sharp transition at a Rossby number of 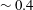${\sim}0.4$. Again, helical axial columnar structures are found for lower Rossby numbers, and there is strong evidence that these columns are created by inertial waves, at least on short time scales. We perform direct numerical simulations of the flow induced by a layer of buoyant anomalies subject to strong rotation, inspired by the equatorially biased heat flux in convective planetary dynamos. We assess the role of inertial waves in generating columnar structures. At high rotation rates (or weak forcing) we find columnar flow structures that segregate helicity either side of the buoyant layer, whose axial length scale increases linearly, as predicted by the theory of low-frequency inertial waves. As the rotation rate is weakened and the magnitude of the buoyant perturbations is increased, we identify a portion of the flow which is more strongly three-dimensional. We show that the flow in this region is turbulent, and has a Rossby number above a critical value 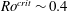$Ro^{crit}\sim 0.4$, consistent with previous findings in rotating turbulence. We suggest that the discrepancy between the transition value found here (and in rotating turbulence experiments), and that seen in the numerical dynamos (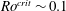$Ro^{crit}\sim 0.1$), is a result of a different choice of the length scale used to define the local $Ro$. We show that when a proxy for the flow length scale perpendicular to the rotation axis is used in this definition, the numerical dynamo transition lies at 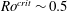$Ro^{crit}\sim 0.5$. Based on this we hypothesise that inertial waves, continually launched by buoyant anomalies, sustain the columnar structures in dynamo simulations, and that the transition documented in these simulations is due to the inability of inertial waves to propagate for 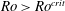$Ro>Ro^{crit}$.

JFM classification

Geophysical and Geological Flows: Geodynamo Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 874 , 10 September 2019 , pp. 995 - 1020
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baqui, Y. B. & Davidson, P. A. 2015 A phenomenological theory of rotating turbulence. Phys. Fluids 27 (2), 025107.10.1063/1.4907671Google Scholar
Bardsley, O. P. & Davidson, P. A. 2016 Inertial–Alfvén waves as columnar helices in planetary cores. J. Fluid Mech. 805, R2.10.1017/jfm.2016.577Google Scholar
Bardsley, O. P. & Davidson, P. A. 2017 The dispersion of magnetic-Coriolis waves in planetary cores. Geophys. J. Intl 210 (1), 18–26.10.1093/gji/ggx143Google Scholar
Bouffard, M., Labrosse, S., Choblet, G., Fournier, A., Aubert, J. & Tackley, P. J. 2017 A particle-in-cell method for studying double-diffusive convection in the liquid layers of planetary interiors. Comput. Phys. 346, 552–571.Google Scholar
Bracewell, R. N. 1986 The Fourier Transform and its Applications, 2nd edn. McGraw-Hill.Google Scholar
Busse, F. H. 1975 A model of the geodynamo. Geophys. J. Intl 42 (2), 437–459.Google Scholar
Christensen, U. R. & Aubert, J. 2006 Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Intl 166 (1), 97–114.10.1111/j.1365-246X.2006.03009.xGoogle Scholar
Dallas, V. & Tobias, S. M. 2016 Forcing-dependent dynamics and emergence of helicity in rotating turbulence. J. Fluid Mech. 798, 682–695.10.1017/jfm.2016.341Google Scholar
Davidson, P. A. 2013 Turbulence in Rotating, Stratified and Electrically Conducting Fluids. Cambridge University Press.10.1017/CBO9781139208673Google Scholar
Davidson, P. A. 2014 The dynamics and scaling laws of planetary dynamos driven by inertial waves. Geophys. J. Intl 198 (3), 1832–1847.10.1093/gji/ggu220Google Scholar
Davidson, P. A. 2016 Dynamos driven by helical waves: scaling laws for numerical dynamos and for the planets. Geophys. J. Intl 207 (2), 680–690.Google Scholar
Davidson, P. A. & Ranjan, A. 2015 Planetary dynamos driven by helical waves – II. Geophys. J. Intl 202 (3), 1646–1662.Google Scholar
Davidson, P. A. & Ranjan, A. 2018 Are planetary dynamos driven by helical waves? J. Plasma Phys. 84 (3), 735840304.Google Scholar
Davidson, P. A., Staplehurst, P. J. & Dalziel, S. B. 2006 On the evolution of eddies in a rapidly rotating system. J. Fluid Mech. 557, 135–144.10.1017/S0022112006009827Google Scholar
Dormy, E., Oruba, L. & Petitdemange, L. 2018 Three branches of dynamo action. Fluid Dyn. Res. 50 (1), 011415.Google Scholar
Driscoll, P. & Olson, P. 2009 Effects of buoyancy and rotation on the polarity reversal frequency of gravitationally driven numerical dynamos. Geophys. J. Intl 178 (3), 1337–1350.Google Scholar
Garcia, F., Oruba, L. & Dormy, E. 2017 Equatorial symmetry breaking and the loss of dipolarity in rapidly rotating dynamos. Geophys. Astrophys. Fluid Dyn. 111 (5), 380–393.10.1080/03091929.2017.1347785Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Gubbins, D. 2001 The Rayleigh number for convection in the Earth’s core. Phys. Earth Planet. Inter. 128 (1-4), 3–12.Google Scholar
Hide, R., Ibbetson, A. & Lighthill, M. J. 1968 On slow transverse flow past obstacles in a rapidly rotating fluid. J. Fluid Mech. 32 (2), 251–272.10.1017/S0022112068000704Google Scholar
Jackson, A., Jonkers, A. R. T. & Walker, M. R. 2000 Four centuries of geomagnetic secular variation from historical records. Phil. Trans. R. Soc. Lond. A 358 (1768), 957–990.Google Scholar
Kageyama, A., Miyagoshi, T. & Sato, T. 2008 Formation of current coils in geodynamo simulations. Nature 454 (7208), 1106–1109.Google Scholar
Kutzner, C. & Christensen, U. R. 2002 From stable dipolar towards reversing numerical dynamos. Phys. Earth Planet. Inter. 131 (1), 29–45.Google Scholar
Lighthill, M. J. 1970 The theory of trailing Taylor columns. Proc. Camb. Phil. Soc. 68 (2), 485–491.10.1017/S0305004100046296Google Scholar
Mininni, P. D., Alexakis, A. & Pouquet, A. 2009 Scale interactions and scaling laws in rotating flows at moderate Rossby numbers and large Reynolds numbers. Phys. Fluids 21 (1), 015108.10.1063/1.3064122Google Scholar
Mininni, P. D. & Pouquet, A. 2009a Finite dissipation and intermittency in magnetohydrodynamics. Phys. Rev. E 80 (2), 025401.Google Scholar
Mininni, P. D. & Pouquet, A. 2009b Helicity cascades in rotating turbulence. Phys. Rev. E 79 (2), 026304.Google Scholar
Olson, P. & Christensen, U. R. 2006 Dipole moment scaling for convection-driven planetary dynamos. Earth Planet. Sci. Lett. 250 (3-4), 561–571.Google Scholar
Olson, P., Christensen, U. R. & Glatzmaier, G. A. 1999 Numerical modeling of the geodynamo: mechanisms of field generation and equilibration. J. Geophys. Res. 104 (B5), 10383–10404.10.1029/1999JB900013Google Scholar
Oruba, L. & Dormy, E. 2014 Transition between viscous dipolar and inertial multipolar dynamos. Geophys. Res. Lett. 41 (20), 7115–7120.10.1002/2014GL062069Google Scholar
Ranjan, A. & Davidson, P. A. 2014 Evolution of a turbulent cloud under rotation. J. Fluid Mech. 756, 488–509.10.1017/jfm.2014.457Google Scholar
Ranjan, A., Davidson, P. A., Christensen, U. R. & Wicht, J. 2018 Internally driven inertial waves in geodynamo simulations. Geophys. J. Intl 213 (2), 1281–1295.Google Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76 (9), 096801.Google Scholar
Sahoo, G., Perlekar, P. & Pandit, R. 2011 Systematics of the magnetic-Prandtl-number dependence of homogeneous, isotropic magnetohydrodynamic turbulence. New J. Phys. 13 (1), 013036.Google Scholar
Sakuraba, A. & Roberts, P. H. 2009 Generation of a strong magnetic field using uniform heat flux at the surface of the core. Nat. Geosci. 2 (11), 802–805.Google Scholar
Sano, M., Wu, X. Z. & Libchaber, A. 1989 Turbulence in helium-gas free convection. Phys. Rev. A 40 (11), 6421–6430.10.1103/PhysRevA.40.6421Google Scholar
Schaeffer, N., Jault, D., Nataf, H.-C. & Fournier, A. 2017 Turbulent geodynamo simulations: a leap towards Earth’s core. Geophys. J. Intl 211 (1), 1–29.Google Scholar
Sheyko, A., Finlay, C. C. & Jackson, A. 2016 Magnetic reversals from planetary dynamo waves. Nature 539 (7630), 551–554.10.1038/nature19842Google Scholar
Soderlund, K. M., King, E. M. & Aurnou, J. M. 2012 The influence of magnetic fields in planetary dynamo models. Earth Planet. Sci. Lett. 333, 9–20.Google Scholar
Soderlund, K. M., King, E. M. & Aurnou, J. M. 2014 Corrigendum to ‘the influence of magnetic fields in planetary dynamo models’ [Earth Planet. Sci. Lett. 333–334 (2012) 9–20]. Earth Planet. Sci. Lett. 392, 121–123.Google Scholar
Sreenivasan, B. & Davidson, P. A. 2008 On the formation of cyclones and anticyclones in a rotating fluid. Phys. Fluids 20 (8), 085104.10.1063/1.2966400Google Scholar
Sreenivasan, B. & Jones, C. A. 2011 Helicity generation and subcritical behaviour in rapidly rotating dynamos. J. Fluid Mech. 688, 5–30.Google Scholar
Staplehurst, P. J., Davidson, P. A. & Dalziel, S. B. 2008 Structure formation in homogeneous freely decaying rotating turbulence. J. Fluid Mech. 598, 81–105.Google Scholar
Sumita, I. & Olson, P. 2000 Laboratory experiments on high Rayleigh number thermal convection in a rapidly rotating hemispherical shell. Phys. Earth Planet. Inter. 117 (1-4), 153–170.10.1016/S0031-9201(99)00094-1Google Scholar
Yarom, E. & Sharon, E. 2014 Experimental observation of steady inertial wave turbulence in deep rotating flows. Nat. Phys. 10 (7), 510–514.Google Scholar
Yeung, P. K. & Zhou, Y. 1998 Numerical study of rotating turbulence with external forcing. Phys. Fluids 10 (11), 2895–2909.Google Scholar