Article contents
Pilot-wave dynamics in a rotating frame: the onset of orbital instability
Published online by Cambridge University Press: 10 October 2023
Abstract
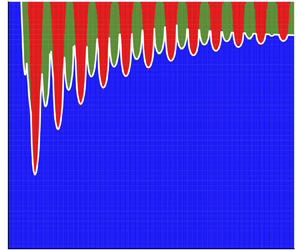
We report the results of a theoretical investigation of the stability of a hydrodynamic analogue of Landau levels, specifically circular orbits arising when a millimetric droplet self-propels along the surface of a vibrating, rotating liquid bath. Our study elucidates the form of the stability diagram characterising the critical memory at which circular orbits destabilise, and the form of instability. Particular attention is given to rationalising observations reported in prior experimental works, including the prevalence of resonant wobbling instabilities, in which the instability frequency is approximately twice the orbital frequency. We also explore the physical mechanism responsible for the onset of instability. Specifically, we compare the efficacy of different heuristic arguments proposed in prior studies, including propositions that the most unstable orbits arise when their radii correspond to the zeros of Bessel functions or when their associated wave intensity is extremised. We establish a new relation between orbital stability and the mean wave field, which supersedes existing heuristic arguments and suggests a rationale for the alternate wobbling and monotonic instabilities arising at onset as the orbital radius is increased progressively.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 6
- Cited by


