Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-14T07:04:37.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Plume emission statistics in turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  28 April 2015

Erwin P. van der Poel ,
Roberto Verzicco ,
Siegfried Grossmann  and
Detlef Lohse
Erwin P. van der Poel*
Affiliation:
Physics of Fluids group, Department of Science and Technology, Mesa+ Institute and J.M. Burgers Centre of Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
Roberto Verzicco
Affiliation:
Physics of Fluids group, Department of Science and Technology, Mesa+ Institute and J.M. Burgers Centre of Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands Dipartimento di Ingegneria Industriale, University of Rome ‘Tor Vergata’, Via del Politecnico 1, Roma 00133, Italy
Siegfried Grossmann
Affiliation:
Fachbereich Physik, Philipps-Universität Marburg, Renthof 6, D-35032 Marburg, Germany
Detlef Lohse
Affiliation:
Physics of Fluids group, Department of Science and Technology, Mesa+ Institute and J.M. Burgers Centre of Fluid Dynamics, University of Twente, PO Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: e.p.vanderpoel@utwente.nl
Get access Rights & Permissions [Opens in a new window]

Abstract

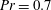Direct numerical simulations (DNS) of turbulent thermal convection in a $\mathit{Pr}=0.7$ fluid up to $\mathit{Ra}=10^{12}$ are used to study the statistics of thermal plumes. At various vertical locations in a cylindrical set-up with aspect ratio 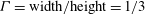${\it\Gamma}=\text{width}/\text{height}=1/3$, plumes are identified and their properties extracted. It is found that plumes are much less likely to be emitted from plate regions with large wind shear. Close to the plates, the plumes have a unimodal log–normal distribution, whereas at more central locations the distribution becomes weakly bimodal, which can be traced back to clustering of the plumes and influence of the large-scale circulation. The number of hot plumes decreases with height. The width of the plumes scales with 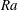$\mathit{Ra}$ approximately as 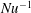$\mathit{Nu}^{-1}$, indicating that it is determined by the thermal boundary layer thickness.

JFM classification

Convection: Plumes/thermals Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 772 , 10 June 2015 , pp. 5 - 15
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70, 4067–4070.CrossRefGoogle ScholarPubMed
Bosbach, J., Weiss, S. & Ahlers, G. 2012 Plume fragmentation by bulk interactions in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 054501.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X. Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Ching, E. S. C., Guo, H., Shang, X. D., Tong, P. & Xia, K.-Q. 2004 Extraction of plumes in turbulent thermal convection. Phys. Rev. Lett. 93, 124501.Google Scholar
Eckhardt, B., Grossmann, S. & Lohse, D. 2007 Torque scaling in turbulent Taylor–Couette flow between independently rotating cylinders. J. Fluid Mech. 581, 221–250.Google Scholar
Emran, M. S. & Schumacher, J. 2012 Conditional statistics of thermal dissipation rate in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 108.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement induced heat transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.Google Scholar
Hunt, J. C. R., Vrieling, A. J., Nieuwstadt, F. T. M. & Fernando, H. J. S. 2003 The influence of the thermal diffusivity of the lower boundary on eddy motion in convection. J. Fluid Mech. 491, 183–205.CrossRefGoogle Scholar
Kaczorowski, M. & Wagner, C. 2009 Analysis of the thermal plumes in turbulent Rayleigh–Bénard convection based on well-resolved numerical simulations. J. Fluid Mech. 618, 89–112.Google Scholar
Kadanoff, L. P. 2001 Turbulent heat flow: structures and scaling. Phys. Today 54 (8), 34–39.Google Scholar
Kraichnan, R. H. 1962 Turbulent thermal convection at arbritrary Prandtl number. Phys. Fluids 5, 1374–1389.CrossRefGoogle Scholar
Lohse, D. & Xia, K. Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.Google Scholar
Ostilla-Mónico, R., van der Poel, E. P., Verzicco, R., Grossmann, S. & Lohse, D. 2014 Boundary layer dynamics at the transition between the classical and the ultimate regime of Taylor–Couette flow. Phys. Fluids 26, 015114.Google Scholar
Parodi, A., von Hardenberg, J., Passoni, G., Provenzale, A. & Spiegel, E. A. 2004 Clustering of plumes in turbulent convection. Phys. Rev. Lett. 92, 194503.Google Scholar
Puthenveettil, B. A. & Arakeri, J. H. 2005 Plume structure in high-Rayleigh-number convection. J. Fluid Mech. 542, 217–249.Google Scholar
Sano, M., Wu, X. Z. & Libchaber, A. 1989 Turbulence in helium-gas free convection. Phys. Rev. A 40, 6421–6430.Google Scholar
Shishkina, O. & Wagner, C. 2008 Analysis of sheet like thermal plumes in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 599, 383–404.CrossRefGoogle Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh number convection. Phys. Rev. A 42, 3650–3653.Google Scholar
Siggia, E. D. 1994 High Rayleigh number convection. Annu. Rev. Fluid Mech. 26, 137–168.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011 Prandtl number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid Mech. 688, 31–43.CrossRefGoogle Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulence convection in water. Phys. Rev. E 47, R2253–R2256.Google Scholar
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.Google Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.Google Scholar
Xi, H. D., Lam, S. & Xia, K.-Q. 2004 From laminar plumes to organized flows: the onset of large-scale circulation in turbulent thermal convection. J. Fluid Mech. 503, 47–56.CrossRefGoogle Scholar
Zhou, Q., Sun, C. & Xia, K.-Q. 2007 Morphological evolution of thermal plumes in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 074501.Google Scholar
Zhou, Q. & Xia, K.-Q. 2010 Physical and geometrical properties of thermal plumes in turbulent Rayleigh–Bénard convection. New J. Phys. 12, 075006.Google Scholar