Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T08:31:18.307Z Has data issue: false hasContentIssue false
  • English
  • Français

Prediction of compressible turbulent boundary layer via a symmetry-based length model

Published online by Cambridge University Press:  22 October 2018

Zhen-Su She Open the ORCID record for Zhen-Su She [Opens in a new window] ,
Hong-Yue Zou ,
Meng-Juan Xiao ,
Xi Chen  and
Fazle Hussain Open the ORCID record for Fazle Hussain [Opens in a new window]
Zhen-Su She*
Affiliation:
State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics, College of Engineering, Peking University, Beijing, 100871, China
Hong-Yue Zou
Affiliation:
State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics, College of Engineering, Peking University, Beijing, 100871, China
Meng-Juan Xiao
Affiliation:
State Key Laboratory for Turbulence and Complex Systems and Department of Mechanics, College of Engineering, Peking University, Beijing, 100871, China
Xi Chen
Affiliation:
Department of Mechanical Engineering, Texas Tech University, TX 79409-1021, USA
Fazle Hussain
Affiliation:
Department of Mechanical Engineering, Texas Tech University, TX 79409-1021, USA
*
†Email address for correspondence: she@pku.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

A recently developed symmetry-based theory is extended to derive an algebraic model for compressible turbulent boundary layers (CTBL) – predicting mean profiles of velocity, temperature and density – valid from incompressible to hypersonic flow regimes, thus achieving a Mach number (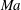$Ma$) invariant description. The theory leads to a multi-layer analytic form of a stress length function which yields a closure of the mean momentum equation. A generalized Reynolds analogy is then employed to predict the turbulent heat transfer. The mean profiles and the friction coefficient are compared with direct numerical simulations of CTBL for a range of 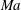$Ma$ from 0 (e.g. incompressible) to 6.0 (e.g. hypersonic), with an accuracy notably superior to popular current models such as Baldwin–Lomax and Spalart–Allmaras models. Further analysis shows that the modification is due to an improved eddy viscosity function compared to competing models. The results confirm the validity of our 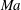$Ma$-invariant stress length function and suggest the path for developing turbulent boundary layer models which incorporate the multi-layer structure.

JFM classification

Compressible Flows: Compressible boundary layers Turbulent Flows: Compressible turbulence Turbulent Flows: Turbulence modelling
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 857 , 25 December 2018 , pp. 449 - 468
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baldwin, B. S. & Lomax, H. 1978 Thin-layer approximation and algebraic model for separated turbulent flows. AIAA J., 78-257.Google Scholar
Bradshaw, P. 1977 Compressible turbulent shear layers. Annu. Rev. Fluid Mech. 9, 33–52.Google Scholar
Brun, C., Boiarciuc, M. P., Haberkorn, M. & Comte, P. 2008 Large eddy simulation of compressible channel flow. Theor. Comput. Fluid Dyn. 22 (3–4), 189–212.Google Scholar
Catris, S. & Aupoix, B. 2000 Density corrections for turbulence models. Aerosp. Sci. Technol. 4 (1), 1–11.Google Scholar
Chen, X., Hussain, F. & She, Z. S. 2016a Bulk flow scaling for turbulent channel and pipe flows. Europhys. Lett. 115 (34001).Google Scholar
Chen, X., Hussain, F. & She, Z. S. 2016b Predictions of canonical wall-bounded turbulent flows via a modified k-𝜔 equation. J. Turbul. 18 (1), 1–35.Google Scholar
Chen, X., Hussain, F. & She, Z. S. 2018 Quantifying wall turbulence via a symmetry approach. Part 2. Reynolds stresses. J. Fluid Mech. 850, 401–438.Google Scholar
Chen, X. & She, Z. S. 2016 Analytic prediction for planar turbulent boundary layers. Sci. China Phys. Mech. 59 (11:114711).Google Scholar
Chen, X., Wei, B. B., Hussain, F. & She, Z. S. 2016c Anomalous dissipation and kinetic-energy distribution in pipes at very high Reynolds numbers. Phys. Rev. E 93 (1), 011102.Google Scholar
Deck, S., Duveau, P., D’Espiney, P. & Guillen, P. 2002 Development and application of Spalart–Callmaras one equation turbulence model to three-dimensional supersonic complex configurations. Aerosp. Sci. Technol. 6 (3), 171–183.Google Scholar
Dong, M. & Li, X. L. 2011 Problems of the conventional BL model as applied to super/hypersonic turbulent boundary layers and its improvements. Sci. China Phys. Mech. 54 (10), 1889–1898.Google Scholar
Dong, M. & Zhou, H. 2010 The improvement of turbulence modelling for the aerothermal computation of hypersonic turbulent boundary layers. Sci. China Phys. Mech. 53 (2), 369–379.Google Scholar
van Driest, E. R. 1951 Turbulent boundary layer in compressible fluids. J. Aeronaut. Sci. 18 (3), 145–160.Google Scholar
van Driest, E. R. 1956 On turbulent flow near a wall. J. Aeronaut. Sci. 23 (11), 1007–1011.Google Scholar
Duan, L.2011 DNS of hypersonic turbulent boundary layers. PhD thesis, Princeton University.Google Scholar
Duan, L., Beekman, I. & Martin, M. P. 2010 Direct numerical simulation of hypersonic turbulent boundary layers. Part 2. Effect of wall temperature. J. Fluid Mech. 655, 419–445.Google Scholar
Gatski, T. B. & Bonnet, J. P. 2013 Compressibility, Turbulence and High Speed Flow. Academic Press.Google Scholar
Gatski, T. B. & Erlebacher, G.2002 Numerical simulation of a spatially evolving supersonic turbulent boundary layer. NASA/TM-2002-211934.Google Scholar
Hadjadj, A., Ben-Nasr, O., Shadloo, M. S. & Chaudhuri, A. 2015 Effect of wall temperature in supersonic turbulent boundary layers: a numerical study. Intl J. Heat Mass Transfer 81 (81), 426–438.Google Scholar
Huang, P. G., Bradshaw, P. & Coakley, T. J. 1994 Turbulence models for compressible boundary layers. AIAA J. 32 (4), 735–740.Google Scholar
Huang, P. G., Coleman, G. N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.Google Scholar
von Karman, T. 1930 Mechanische ähnlichkeit und turbulenz, nachr. ges. wiss. göttingen. Proc. 3. Int. Cong. Appl. Mech. 58–76, 322–346.Google Scholar
Li, X. L., Fu, D. X. & Ma, Y. W. 2006 Direct numerical simulation of a spatially evolving supersonic turbulent boundary layer at Ma = 6. Chin. Phys. Lett. 23 (6), 1519.Google Scholar
Li, X. L., Ma, Y. W. & Fu, D. X. 2001 DNS and scaling law analysis of compressible turbulent channel flow. Sci. China A: Maths 44 (5), 645–654.Google Scholar
Morkovin, M. V. 1962 Effects of compressibility on turbulent flows. In Mecanique de la Turbulence (ed. Favre, A. J.), pp. 367–380. CNRS, Paris.Google Scholar
Nagib, H. M., Monkewitz, P. A., Mascotelli, L., Fiorini, T., Bellani, G., Zheng, X. & Talamelli, A.2017 Karman ‘constant’ revisited and contrasted to log-layer Karman constant at ciclope. 10th International Symposium on Turbulence and Shear Flow Phenomena, Chicago, USA.Google Scholar
Pirozzoli, S., Grasso, F. & Gatski, T. B. 2004 Direct numerical simulation and analysis of a spatially evolving supersonic turbulent boundary layer at Ma = 2. 25. Phys. Fluids 16, 530–545.Google Scholar
Prandtl, L. 1925 Bericht uber untersuchungen zur ausgebildeten turbulenz. Z. Angew. Math. Mech. 5, 136–139.Google Scholar
Roy, C. J. & Blottner, F. G. 2006 Review and assessment of turbulence models for hypersonic flows. Prog. Aerosp. Sci. 42, 469–530.Google Scholar
Rumsey, C. L. 2010 Compressibility considerations for k-omega turbulence models in hypersonic boundary-layer applications. J. Spacecr. Rockets 47 (1).Google Scholar
Schlatter, P., Li, Q., Brethouwer, G., Johansson, A. V. & Henningson, D. S. 2010 Simulations of spatially evolving turbulent boundary layers up to Re 𝜃 = 4300. Intl J. Heat Fluid Flow 31 (3), 251–261.Google Scholar
Shadloo, M. S., Hadjadj, A. & Hussain, F. 2015 Statistical behavior of supersonic turbulent boundary layers with heat transfer at M ∞ = 2 mathcontainer loading mathjax. Intl J. Heat Fluid Flow 53, 113–134.Google Scholar
She, Z. S., Chen, X. & Hussain, F. 2017 Quantifying wall turbulence via a symmetry approach: a Lie group theory. J. Fluid Mech. 827, 322–356.Google Scholar
She, Z. S., Chen, X., Wu, Y. & Hussain, F. 2010 New perspective in statistical modeling of wall-bounded turbulence. Acta Mech. Sin. 26 (6), 847–861.Google Scholar
She, Z. S., Wu, Y., Chen, X. & Hussain, F. 2012 A multi-state description of roughness effects in turbulent pipe flow. New J. Phys. 14 (9), 093054.Google Scholar
Slotnick, J., Khodadoust, A., Alonso, J., Darmofal, D., Gropp, W., Lurie, E. & Mavriplis, D.2014 CFD vision 2030 study: a path to revolutionary computational aerosciences. NASA/CR-2014-218178.Google Scholar
Smits, A. J. & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer.Google Scholar
Spalart, P. 2006 Turbulence are we getting smarter. In Fluid Dynamics Award Lecture, 36th Fluid Dynamics Conference and Exhibit, San Francisco, CA 5 (8), pp. 5–8.Google Scholar
Spalart, P. & Allmaras, S. 1992 A one-equation turbulence model for aerodynamic flows. In 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, p. 439.Google Scholar
Trettel, A. & Larsson, J. 2016 Mean velocity scaling for compressible wall turbulence with heat transfer. Phys. Fluids 28 (2), 026102.Google Scholar
Vallikivi, M., Hultmark, M. & Smits, A. J. 2015 Turbulent boundary layer statistics at very high Reynolds number. J. Fluid Mech. 779, 371–389.Google Scholar
Walz, A. 1966 Stromungs-und Temperaturgrenzschichten, Braun (translation in Boundary Layers of Flow and Temperature, MIT Press, 1969).Google Scholar
Wilcox, D. C. 2006 Turbulence modeling for CFD. DCW industries La Canada.Google Scholar
Wu, B.2016 Symmetry and invariant mean velocity in compressible turbulent boundary layer. PhD thesis. Peking University.Google Scholar
Wu, B., Bi, W. T., Hussain, F. & She, Z. S. 2017 On the invariant mean velocity profile for compressible turbulent boundary layers. J. Turbul. 18 (2), 186–202.Google Scholar
Xiao, M. J. & She, Z. S. 2016 A new algebraic transition model based on stress length function. Bull. Am. Phys. Soc. 61, H29.002.Google Scholar
Xiao, M. J. & She, Z. S. 2017 A new algebraic turbulence model for accurate description of airfoil flows. Bull. Am. Phys. Soc. 62, Q29.011.Google Scholar
Zhang, Y. S., Bi, W. T., Hussain, F., Li, X. L. & She, Z. S. 2012 Mach-number-invariant mean-velocity profile of compressible turbulent boundary layers. Phys. Rev. Lett. 109, 054502.Google Scholar
Zhang, Y. S., Bi, W. T., Hussain, F. & She, Z. S. 2014 A generalized Reynolds analogy for compressible wall-bounded turbulent flows. J. Fluid Mech. 739, 392–420.Google Scholar