1. Introduction
In one of his seminal works, Lord Rayleigh (Reference Rayleigh1879) showed that a free spherical drop held by surface tension will oscillate about its equilibrium shape with characteristic frequency
and mode shape ![]() $Y_k^{\ell }$ given by the spherical harmonics of degree
$Y_k^{\ell }$ given by the spherical harmonics of degree ![]() $k$ and order
$k$ and order ![]() $\ell$, in what has now become one of the canonical problems in drop dynamics. Here
$\ell$, in what has now become one of the canonical problems in drop dynamics. Here ![]() $\varrho, \sigma, R$ are the density, surface tension and drop radius, respectively. The Rayleigh spectrum (1.1) has stood the test of time having been verified in both terrestrial (Trinh & Wang Reference Trinh and Wang1982) and microgravity (Wang, Anilkumar & Lee Reference Wang, Anilkumar and Lee1996) conditions. Recent interest in drop oscillations has focused on the role substrate contact has on the frequency spectrum for a variety of wetting conditions (Chebel, Risso & Masbernat Reference Chebel, Risso and Masbernat2011; Sharp, Farmer & Kelly Reference Sharp, Farmer and Kelly2011; Sharp Reference Sharp2012; Sakakeeny et al. Reference Sakakeeny, Deshpande, Deb, Alvarado and Ling2021). Such drop wetting interactions are typified in the problem of sessile-drop oscillations. Our interest is in the symmetry decomposition of the Rayleigh spectrum and how it relates to the sessile-drop spectrum.
$\varrho, \sigma, R$ are the density, surface tension and drop radius, respectively. The Rayleigh spectrum (1.1) has stood the test of time having been verified in both terrestrial (Trinh & Wang Reference Trinh and Wang1982) and microgravity (Wang, Anilkumar & Lee Reference Wang, Anilkumar and Lee1996) conditions. Recent interest in drop oscillations has focused on the role substrate contact has on the frequency spectrum for a variety of wetting conditions (Chebel, Risso & Masbernat Reference Chebel, Risso and Masbernat2011; Sharp, Farmer & Kelly Reference Sharp, Farmer and Kelly2011; Sharp Reference Sharp2012; Sakakeeny et al. Reference Sakakeeny, Deshpande, Deb, Alvarado and Ling2021). Such drop wetting interactions are typified in the problem of sessile-drop oscillations. Our interest is in the symmetry decomposition of the Rayleigh spectrum and how it relates to the sessile-drop spectrum.
Bostwick & Steen (Reference Bostwick and Steen2014) have computed the frequency spectrum for the sessile drop on a flat substrate showing how it depends upon the static contact-angle ![]() $\alpha$ and contact-line (CL) mobility resistance parameter
$\alpha$ and contact-line (CL) mobility resistance parameter ![]() $\varLambda$ associated with the ‘Hocking condition’ (Davis Reference Davis1980; Hocking Reference Hocking1987). Limiting cases correspond to freely moving
$\varLambda$ associated with the ‘Hocking condition’ (Davis Reference Davis1980; Hocking Reference Hocking1987). Limiting cases correspond to freely moving ![]() $\varLambda =0$ and pinned
$\varLambda =0$ and pinned ![]() $\varLambda =\infty$ CLs with intermediate cases
$\varLambda =\infty$ CLs with intermediate cases ![]() $\varLambda \neq 0,\infty$ corresponding to stick-slip behaviours (Shaikeea et al. Reference Shaikeea, Basu, Tyagi, Sharma, Hans and Bansal2017). We note an analytical-based solution method has recently been proposed by Sharma & Wilson (Reference Sharma and Wilson2021) for pinned drops. The predictions of Bostwick & Steen (Reference Bostwick and Steen2014) have been verified for drops with pinned CLs (
$\varLambda \neq 0,\infty$ corresponding to stick-slip behaviours (Shaikeea et al. Reference Shaikeea, Basu, Tyagi, Sharma, Hans and Bansal2017). We note an analytical-based solution method has recently been proposed by Sharma & Wilson (Reference Sharma and Wilson2021) for pinned drops. The predictions of Bostwick & Steen (Reference Bostwick and Steen2014) have been verified for drops with pinned CLs (![]() $\varLambda =\infty$) by Chang et al. (Reference Chang, Bostwick, Steen and Daniel2013, Reference Chang, Bostwick, Daniel and Steen2015) over a range of
$\varLambda =\infty$) by Chang et al. (Reference Chang, Bostwick, Steen and Daniel2013, Reference Chang, Bostwick, Daniel and Steen2015) over a range of ![]() $\alpha$. The structure of the spectrum is rich and includes predictions such as splitting of the Rayleigh drop degeneracy, spectral reordering and mode mixing, all of which have been verified experimentally. Notably, Steen, Chang & Bostwick (Reference Steen, Chang and Bostwick2019) have introduced an organizational structure for the sessile-drop spectrum introducing the ‘periodic table of droplet motions’. Their modal classification system is inherited from the Rayleigh drop and restricts mode numbers
$\alpha$. The structure of the spectrum is rich and includes predictions such as splitting of the Rayleigh drop degeneracy, spectral reordering and mode mixing, all of which have been verified experimentally. Notably, Steen, Chang & Bostwick (Reference Steen, Chang and Bostwick2019) have introduced an organizational structure for the sessile-drop spectrum introducing the ‘periodic table of droplet motions’. Their modal classification system is inherited from the Rayleigh drop and restricts mode numbers ![]() $k+\ell =\mathbb {Z}^{+}_{even}$, as required to enforce the no-penetration condition at the solid support.
$k+\ell =\mathbb {Z}^{+}_{even}$, as required to enforce the no-penetration condition at the solid support.
The Rayleigh drop modes for the full sphere are given by the spherical harmonics and defined by the mode number pair ![]() $[k,\ell ]$ with
$[k,\ell ]$ with ![]() $\ell \leqslant k$. Note the spectrum (1.1) is degenerate with respect to azimuthal mode number
$\ell \leqslant k$. Note the spectrum (1.1) is degenerate with respect to azimuthal mode number ![]() $l$. Figure 1 plots the Rayleigh modes with (
$l$. Figure 1 plots the Rayleigh modes with (![]() $a$)
$a$) ![]() $k+\ell =\mathbb {Z}^{+}_{even}$ and (
$k+\ell =\mathbb {Z}^{+}_{even}$ and (![]() $b$)
$b$) ![]() $k+\ell =\mathbb {Z}^{+}_{odd}$ and their corresponding symmetry extension about the equatorial plane that defines the hemispherical
$k+\ell =\mathbb {Z}^{+}_{odd}$ and their corresponding symmetry extension about the equatorial plane that defines the hemispherical ![]() $\alpha =90^{\circ }$ drop. For the case
$\alpha =90^{\circ }$ drop. For the case ![]() $k+\ell =\mathbb {Z}^{+}_{even}$, the flow field naturally satisfies the no-flux (or no-penetration) condition on the solid support and has a CL that freely moves with fixed CA and the sessile-drop modes for this case
$k+\ell =\mathbb {Z}^{+}_{even}$, the flow field naturally satisfies the no-flux (or no-penetration) condition on the solid support and has a CL that freely moves with fixed CA and the sessile-drop modes for this case ![]() $(\alpha =90^{\circ },\varLambda =0)$ are precisely the Rayleigh modes, as required by symmetry. At this point, it is clear why Steen et al. (Reference Steen, Chang and Bostwick2019) introduced this classification scheme for a sessile drop on a solid support. Interestingly, pinning the CL for a hemispherical drop
$(\alpha =90^{\circ },\varLambda =0)$ are precisely the Rayleigh modes, as required by symmetry. At this point, it is clear why Steen et al. (Reference Steen, Chang and Bostwick2019) introduced this classification scheme for a sessile drop on a solid support. Interestingly, pinning the CL for a hemispherical drop ![]() $\alpha =90^{\circ }$ breaks the azimuthal degeneracy of the Rayleigh spectrum (Chang et al. Reference Chang, Bostwick, Steen and Daniel2013; Bostwick & Steen Reference Bostwick and Steen2014) and for
$\alpha =90^{\circ }$ breaks the azimuthal degeneracy of the Rayleigh spectrum (Chang et al. Reference Chang, Bostwick, Steen and Daniel2013; Bostwick & Steen Reference Bostwick and Steen2014) and for ![]() $\alpha \neq 90^{\circ }, \varLambda \neq 0$ modal ordering can become complex. The
$\alpha \neq 90^{\circ }, \varLambda \neq 0$ modal ordering can become complex. The ![]() $k+\ell =\mathbb {Z}^{+}_{odd}$ symmetry extension results in a flow field with non-zero flux across the solid support and a pinned CL. This situation can be idealized as a sessile drop connected to a fluid reservoir. In this paper, we compute the sessile-drop spectrum for the previously undiscovered
$k+\ell =\mathbb {Z}^{+}_{odd}$ symmetry extension results in a flow field with non-zero flux across the solid support and a pinned CL. This situation can be idealized as a sessile drop connected to a fluid reservoir. In this paper, we compute the sessile-drop spectrum for the previously undiscovered ![]() $k+\ell =\mathbb {Z}^{+}_{odd}$ modes.
$k+\ell =\mathbb {Z}^{+}_{odd}$ modes.

Figure 1. Symmetry decomposition of the Rayleigh drop modes ![]() $[k,\ell ]$ into sessile-drop modes with (
$[k,\ell ]$ into sessile-drop modes with (![]() $a$) even and (
$a$) even and (![]() $b$) odd symmetry about the horizontal midplane for
$b$) odd symmetry about the horizontal midplane for ![]() $\alpha =90^{\circ }$. The
$\alpha =90^{\circ }$. The ![]() $k+\ell =\mathbb {Z}^{+}_{even}$ modes have a contact-line that moves with fixed contact-angle and flow field that naturally satisfies a no-penetration condition on the symmetry plane, whereas the
$k+\ell =\mathbb {Z}^{+}_{even}$ modes have a contact-line that moves with fixed contact-angle and flow field that naturally satisfies a no-penetration condition on the symmetry plane, whereas the ![]() $k+\ell =\mathbb {Z}^{+}_{odd}$ modes have a pinned contact-line with non-zero flux condition on the symmetry plane.
$k+\ell =\mathbb {Z}^{+}_{odd}$ modes have a pinned contact-line with non-zero flux condition on the symmetry plane.
In drop-on-demand inkjet printing (Basaran, Gao & Bhat Reference Basaran, Gao and Bhat2013; Lohse Reference Lohse2022), the shape of the meniscus connected to the printhead can be idealized as a ‘sessile drop connected to a fluid reservoir’ where liquid is transferred from the reservoir by any number of mechanisms into the sessile drop causing pinch-off of the primary drop which deposits on the target. This is also seen in the dripping-to-jetting transition from an orifice (Richards, Beris & Lenhoff Reference Richards, Beris and Lenhoff1995; Utada et al. Reference Utada, Fernandez-Nieves, Stone and Weitz2007), sometimes referred to as a capillary fountain (Schulkes Reference Schulkes1994). The primary differences between the sessile-drop configurations shown in figure 1 are the physics that are enforced. For a sessile drop on a substrate, fluid incompressibility dictates that volume is conserved and any allowable disturbance must also respect volume conservation. In contrast, for a sessile drop connected to a fluid reservoir, volume need not be conserved because of the non-trivial flux from the reservoir. These disturbances are typically referred to as volume and pressure disturbances, respectively (Bostwick & Steen Reference Bostwick and Steen2015). In this work, we focus on these pressure modes for the sessile drop by introducing a lumped-parameter model that relates the reservoir pressure to the drop volume change through an empirical parameter ![]() $\chi$, which is the inverse of the acoustic compliance (Kim et al. Reference Kim, Kim, Shin, Park, Lee, Kang, Shin and Kim2011). Such lumped-parameter models are used to model the physical and electrical coupling of drop-on-demand piezoelectric inkjet printing (Gallas et al. Reference Gallas, Holman, Nishida, Carroll, Sheplak and Cattafesta2003; Kim et al. Reference Kim, Lee, Kim, Kang and Park2014). In our problem, the frequency spectrum depends upon the parameters (
$\chi$, which is the inverse of the acoustic compliance (Kim et al. Reference Kim, Kim, Shin, Park, Lee, Kang, Shin and Kim2011). Such lumped-parameter models are used to model the physical and electrical coupling of drop-on-demand piezoelectric inkjet printing (Gallas et al. Reference Gallas, Holman, Nishida, Carroll, Sheplak and Cattafesta2003; Kim et al. Reference Kim, Lee, Kim, Kang and Park2014). In our problem, the frequency spectrum depends upon the parameters (![]() $\alpha,\varLambda,\chi$).
$\alpha,\varLambda,\chi$).
2. Mathematical formulation
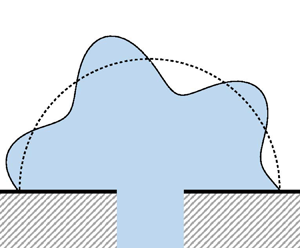
Consider the sessile drop connected to a fluid reservoir shown in figure 2 with equilibrium interface defined as
using arclength-like ![]() $s \in [0,\alpha ]$ and azimuthal angle
$s \in [0,\alpha ]$ and azimuthal angle ![]() $\varphi \in [0,2{\rm \pi} ]$ as generalized surface coordinates. The interface is given a small perturbation
$\varphi \in [0,2{\rm \pi} ]$ as generalized surface coordinates. The interface is given a small perturbation ![]() $\eta (s,\varphi,t)$ that induces a capillary-driven flow
$\eta (s,\varphi,t)$ that induces a capillary-driven flow ![]() $\boldsymbol {v}=\boldsymbol {\nabla } \psi$ defined by the velocity potential
$\boldsymbol {v}=\boldsymbol {\nabla } \psi$ defined by the velocity potential ![]() $\psi$ which satisfies Laplace's equation on the domain
$\psi$ which satisfies Laplace's equation on the domain ![]() $D$ and a kinematic condition on the free surface
$D$ and a kinematic condition on the free surface ![]() $\partial D^{f}$,
$\partial D^{f}$,
The pressure in the drop domain,
is the sum of the linearized Bernoulli pressure and the reservoir pressure ![]() $p_{{reservoir}}$ which we relate to the volume change
$p_{{reservoir}}$ which we relate to the volume change ![]() $\Delta V$ through an empirical parameter
$\Delta V$ through an empirical parameter ![]() $\bar {\chi }$,
$\bar {\chi }$,
 \begin{equation} p_{{reservoir}}=\bar{\chi} \Delta V = \bar{\chi} \int_0^{2{\rm \pi}}\int_{\cos(\alpha)}^{1} R^{2} \eta \,{{\rm d}\kern0.06em x}\,{\rm d}\varphi, \end{equation}
\begin{equation} p_{{reservoir}}=\bar{\chi} \Delta V = \bar{\chi} \int_0^{2{\rm \pi}}\int_{\cos(\alpha)}^{1} R^{2} \eta \,{{\rm d}\kern0.06em x}\,{\rm d}\varphi, \end{equation}
with ![]() ${{\rm d}\kern0.06em x}={\rm d}\cos (s)$. The pressure at the free surface
${{\rm d}\kern0.06em x}={\rm d}\cos (s)$. The pressure at the free surface ![]() $\partial D^{f}$ is given by the linearized Young–Laplace equation,
$\partial D^{f}$ is given by the linearized Young–Laplace equation,
where the right-hand side is the mean curvature of the surface with the first term accounting for radial disturbances and the other two terms accounting for meridional and azimuthal disturbances. For reference, more details are provided in Myshkis et al. (Reference Myshkis, Babskii, Slobozhanin and Tyuptsov1987) for an arbitrary surface. Lastly, we assume a CL condition for ![]() $\eta$ that either (i) freely moves with fixed angle
$\eta$ that either (i) freely moves with fixed angle ![]() $\alpha$ or (ii) is pinned. We do not consider the more general CL speed condition with associated Davis CL dissipation (Bostwick & Steen Reference Bostwick and Steen2014, Reference Bostwick and Steen2016).
$\alpha$ or (ii) is pinned. We do not consider the more general CL speed condition with associated Davis CL dissipation (Bostwick & Steen Reference Bostwick and Steen2014, Reference Bostwick and Steen2016).

Figure 2. Definition sketch showing the (![]() $a$) equilibrium sessile drop with contact-angle
$a$) equilibrium sessile drop with contact-angle ![]() $\alpha$ given by the Young–Dupré equation and (
$\alpha$ given by the Young–Dupré equation and (![]() $b$) disturbed shape in 2-D polar view.
$b$) disturbed shape in 2-D polar view.
2.1. Reduction to operator equation
Dimensionless variables are introduced,
 \begin{align} \rho^{*}=\rho/r, \quad \eta^{*}=\eta/r, \quad t^{*}=t\sqrt{\frac{\sigma}{\varrho r^{3}}},\quad \psi^{*}=\psi \sqrt{\frac{\varrho}{\sigma r}},\quad p^{*}=p\left(\frac{r}{\sigma}\right),\quad \lambda=\omega \sqrt{\frac{\varrho r^{3}}{\sigma }}, \end{align}
\begin{align} \rho^{*}=\rho/r, \quad \eta^{*}=\eta/r, \quad t^{*}=t\sqrt{\frac{\sigma}{\varrho r^{3}}},\quad \psi^{*}=\psi \sqrt{\frac{\varrho}{\sigma r}},\quad p^{*}=p\left(\frac{r}{\sigma}\right),\quad \lambda=\omega \sqrt{\frac{\varrho r^{3}}{\sigma }}, \end{align}and normal modes
written in spherical coordinates ![]() $(\rho,\theta,\varphi )$ and parameterized by dimensionless frequency
$(\rho,\theta,\varphi )$ and parameterized by dimensionless frequency ![]() $\lambda$ and azimuthal mode number
$\lambda$ and azimuthal mode number ![]() $\ell$ are applied to the governing equations. A boundary integral approach is then applied in which the problem is mapped to the free surface (Bostwick & Steen Reference Bostwick and Steen2014),
$\ell$ are applied to the governing equations. A boundary integral approach is then applied in which the problem is mapped to the free surface (Bostwick & Steen Reference Bostwick and Steen2014),
 \begin{align} -\frac{\lambda ^{2}}{\sin^{2}\alpha} \xi-\frac{2{\rm \pi} \chi}{\sin^{4}\alpha} \delta_{\ell,0} \int_{\cos(\alpha)}^{1} \frac{\partial \xi}{\partial n} {{\rm d}x}=\left(2-\frac{\ell^{2}}{\sin^{2}(s)}\right)\frac{\partial \xi}{\partial n}+ \cot(s) \left( \frac{\partial \xi}{\partial n}\right)^{\prime} +\left(\frac{\partial \xi}{\partial n} \right)^{\prime\prime} , \end{align}
\begin{align} -\frac{\lambda ^{2}}{\sin^{2}\alpha} \xi-\frac{2{\rm \pi} \chi}{\sin^{4}\alpha} \delta_{\ell,0} \int_{\cos(\alpha)}^{1} \frac{\partial \xi}{\partial n} {{\rm d}x}=\left(2-\frac{\ell^{2}}{\sin^{2}(s)}\right)\frac{\partial \xi}{\partial n}+ \cot(s) \left( \frac{\partial \xi}{\partial n}\right)^{\prime} +\left(\frac{\partial \xi}{\partial n} \right)^{\prime\prime} , \end{align}
where ![]() $\chi =\bar {\chi } r^{4}\sigma$,
$\chi =\bar {\chi } r^{4}\sigma$, ![]() $'={\rm d}/{\rm d}s$ and
$'={\rm d}/{\rm d}s$ and ![]() $\delta _{\ell,0}$ is the Kronecker delta with
$\delta _{\ell,0}$ is the Kronecker delta with ![]() $\delta _{0,0}=1$,
$\delta _{0,0}=1$, ![]() $\delta _{\ell \neq 0,0}=0$.
$\delta _{\ell \neq 0,0}=0$.
Equation (2.8) is an integrodifferential eigenvalue problem in the scaled frequency ![]() $\lambda$ for the harmonic function
$\lambda$ for the harmonic function ![]() $\xi$, which can be recast in linear operator form,
$\xi$, which can be recast in linear operator form,
with ![]() $\hat {\lambda }\equiv \lambda /\sin \alpha$,
$\hat {\lambda }\equiv \lambda /\sin \alpha$,
and
The Green's function ![]() $G(x,y;\ell )$ is defined as
$G(x,y;\ell )$ is defined as
 \begin{equation} G(x,y;\ell) = \left\{
\begin{array}{@{}ll} \displaystyle\dfrac{1}{1-y^{2}}
\dfrac{U(x;\ell)V(y;\ell)}{W(y;\ell)}, & b< y< x<1 \\
\displaystyle\dfrac{1}{1-y^{2}}
\dfrac{U(y;\ell)V(x;\ell)}{W(y;\ell)}, & b< x< y<1 ,
\end{array} \right. \end{equation}
\begin{equation} G(x,y;\ell) = \left\{
\begin{array}{@{}ll} \displaystyle\dfrac{1}{1-y^{2}}
\dfrac{U(x;\ell)V(y;\ell)}{W(y;\ell)}, & b< y< x<1 \\
\displaystyle\dfrac{1}{1-y^{2}}
\dfrac{U(y;\ell)V(x;\ell)}{W(y;\ell)}, & b< x< y<1 ,
\end{array} \right. \end{equation}
where ![]() $x \equiv \cos (s)$ and
$x \equiv \cos (s)$ and ![]() $b \equiv \cos (\alpha )$,
$b \equiv \cos (\alpha )$, ![]() $U$ and
$U$ and ![]() $V$ are the homogeneous solutions of the curvature operator
$V$ are the homogeneous solutions of the curvature operator ![]() $K$ that satisfy the left-hand and right-hand boundary conditions, respectively,
$K$ that satisfy the left-hand and right-hand boundary conditions, respectively,
and ![]() $W$ is the Wronskian of the solutions
$W$ is the Wronskian of the solutions ![]() $U$ and
$U$ and ![]() $V$. Here
$V$. Here
 \begin{align} \left.\begin{gathered} \displaystyle y_{1}(x;0)=P_{1}(x), \quad y_{2}(x;0)=Q_{1}(x),\quad y_{1}(x;1)=P_{1}^{1}(x),\quad y_{2}(x;1)=Q_{1}^{1}(x),\\ \displaystyle y_{1}(x;\ell\geqslant 2)=(x+\ell)\left(\frac{1-x}{1+x}\right)^{\ell/2}, \quad y_{2}(x;\ell\geqslant 2)=\frac{x-\ell}{2\ell(\ell^{2}-1)}\left(\frac{1+x}{1-x}\right)^{\ell/2}, \end{gathered}\right\} \end{align}
\begin{align} \left.\begin{gathered} \displaystyle y_{1}(x;0)=P_{1}(x), \quad y_{2}(x;0)=Q_{1}(x),\quad y_{1}(x;1)=P_{1}^{1}(x),\quad y_{2}(x;1)=Q_{1}^{1}(x),\\ \displaystyle y_{1}(x;\ell\geqslant 2)=(x+\ell)\left(\frac{1-x}{1+x}\right)^{\ell/2}, \quad y_{2}(x;\ell\geqslant 2)=\frac{x-\ell}{2\ell(\ell^{2}-1)}\left(\frac{1+x}{1-x}\right)^{\ell/2}, \end{gathered}\right\} \end{align}
where ![]() $P_k^{\ell }$ and
$P_k^{\ell }$ and ![]() $Q_k^{\ell }$ are the associated Legendre functions of degree
$Q_k^{\ell }$ are the associated Legendre functions of degree ![]() $k$ and order
$k$ and order ![]() $\ell$ and the parameters
$\ell$ and the parameters ![]() $\tau _{1}$ and
$\tau _{1}$ and ![]() $\tau _{2}$ are related to the CL boundary conditions;
$\tau _{2}$ are related to the CL boundary conditions;
for the pinned CL disturbance (superscript ![]() $p$) and
$p$) and
for the fixed angle disturbance, sometimes referred to as the free disturbance (superscript ![]() $f$).
$f$).
2.2. Rayleigh–Ritz method
We use a Rayleigh–Ritz procedure to compute the spectrum of (2.9) by assuming a solution series
 \begin{equation} \xi=\sum_{j=1}^{N}a_{j}\xi_{j}^{(\ell)},\end{equation}
\begin{equation} \xi=\sum_{j=1}^{N}a_{j}\xi_{j}^{(\ell)},\end{equation}
constructed from basis functions ![]() $\xi _{j}^{(\ell )}$ and applying inner products to generate a set of linear algebraic equations
$\xi _{j}^{(\ell )}$ and applying inner products to generate a set of linear algebraic equations
 \begin{equation} \sum_{j=1}^{N}(m_{ij}^{(\ell)}-\hat{\lambda}^{2} k_{ij}^{(\ell)})a_{j}=0,\end{equation}
\begin{equation} \sum_{j=1}^{N}(m_{ij}^{(\ell)}-\hat{\lambda}^{2} k_{ij}^{(\ell)})a_{j}=0,\end{equation}with
 $$\begin{gather} m_{ij}^{(\ell)}=\int_{b}^{1}\left(\frac{\partial \xi_{i}^{(\ell)}}{\partial n} +\frac{2{\rm \pi} \chi}{\sin^{4}\alpha} \delta_{\ell,0} \int_{b}^{1} G(x,y;\ell) \int_{b}^{1} \frac{\partial \xi_i^{(\ell)}}{\partial n} (z)\,{\rm d}z\right)\xi_{j}^{(\ell)}\,{{\rm d}\kern0.06em x} \,{{\rm d} y}, \end{gather}$$
$$\begin{gather} m_{ij}^{(\ell)}=\int_{b}^{1}\left(\frac{\partial \xi_{i}^{(\ell)}}{\partial n} +\frac{2{\rm \pi} \chi}{\sin^{4}\alpha} \delta_{\ell,0} \int_{b}^{1} G(x,y;\ell) \int_{b}^{1} \frac{\partial \xi_i^{(\ell)}}{\partial n} (z)\,{\rm d}z\right)\xi_{j}^{(\ell)}\,{{\rm d}\kern0.06em x} \,{{\rm d} y}, \end{gather}$$Allowable solutions of (2.8) must necessarily satisfy Laplace's equation and allow for a non-trivial flux across the drop/reservoir boundary. This can be accomplished through judicious choice of basis functions
where ![]() $j+\ell =\mathbb {Z}^{+}_{odd}$.
$j+\ell =\mathbb {Z}^{+}_{odd}$.
The eigenfrequencies ![]() $\lambda _{k,\ell }$ have been calculated using a truncation of
$\lambda _{k,\ell }$ have been calculated using a truncation of ![]() $N=10$ basis functions in the solution series (2.16) for both free and pinned disturbance. The eigenfunction
$N=10$ basis functions in the solution series (2.16) for both free and pinned disturbance. The eigenfunction ![]() $\xi _{k,\ell }$ associated with the eigenfrequencies
$\xi _{k,\ell }$ associated with the eigenfrequencies ![]() $\lambda _{k,\ell }$ and corresponding eigenvector
$\lambda _{k,\ell }$ and corresponding eigenvector ![]() $a_{j}^{(k,\ell )}$ is given by
$a_{j}^{(k,\ell )}$ is given by
 \begin{equation} \xi_{k,\ell}(x)=\sum_{j=1}^{N}a_{j}^{(k,\ell)}\xi_{j}^{(\ell)}(x).\end{equation}
\begin{equation} \xi_{k,\ell}(x)=\sum_{j=1}^{N}a_{j}^{(k,\ell)}\xi_{j}^{(\ell)}(x).\end{equation}3. Results
Mode shapes can be classified using spherical harmonic terminology into zonal (![]() $\ell =0$), rocking (
$\ell =0$), rocking (![]() $\ell =1$) and tesseral (
$\ell =1$) and tesseral (![]() $k\neq \ell$,
$k\neq \ell$, ![]() $\ell \neq 0,1$) modes with
$\ell \neq 0,1$) modes with ![]() $k+\ell =\mathbb {Z}^{+}_{odd}$ (MacRobert Reference MacRobert1967). Typical mode shapes with associated fields (streamlines and pressure) are shown in figure 3. In what follows, we show how the frequency spectrum depends upon
$k+\ell =\mathbb {Z}^{+}_{odd}$ (MacRobert Reference MacRobert1967). Typical mode shapes with associated fields (streamlines and pressure) are shown in figure 3. In what follows, we show how the frequency spectrum depends upon ![]() $\alpha,\chi$ and the CL conditions. The motions are typically oscillatory
$\alpha,\chi$ and the CL conditions. The motions are typically oscillatory ![]() $\lambda ^{2} >0$, but some modes display instability
$\lambda ^{2} >0$, but some modes display instability ![]() $\lambda ^{2}<0$ characterized by instability growth rate
$\lambda ^{2}<0$ characterized by instability growth rate ![]() $-\textrm {Im}[\lambda ]$. Lastly, we note that only the zonal
$-\textrm {Im}[\lambda ]$. Lastly, we note that only the zonal ![]() $\ell =0$ modes depend upon
$\ell =0$ modes depend upon ![]() $\chi$ or allow for non-trivial volume exchange between the drop and reservoir. For
$\chi$ or allow for non-trivial volume exchange between the drop and reservoir. For ![]() $\ell \neq 0$, there is a non-uniform fluid flux across the drop/reservoir boundary in the azimuthal coordinate that necessarily averages out to produce a zero net volume flux between the drop and reservoir.
$\ell \neq 0$, there is a non-uniform fluid flux across the drop/reservoir boundary in the azimuthal coordinate that necessarily averages out to produce a zero net volume flux between the drop and reservoir.

Figure 3. Mode shape ![]() $[k,\ell ]$ classification plotting the interface shape in 2-D polar view (a–c) and 3-D top view (d–f) with associated fields ((g–i), streamlines and pressure contours) for typical (a,d,g) zonal
$[k,\ell ]$ classification plotting the interface shape in 2-D polar view (a–c) and 3-D top view (d–f) with associated fields ((g–i), streamlines and pressure contours) for typical (a,d,g) zonal ![]() $[7,0]$, (b,e,h) rocking
$[7,0]$, (b,e,h) rocking ![]() $[4,1]$ and (c, f,i) tesseral
$[4,1]$ and (c, f,i) tesseral ![]() $[3,2]$ modes.
$[3,2]$ modes.
3.1. Zonal  $\ell =0$ modes
$\ell =0$ modes
Figure 4(a) plots the zonal frequencies ![]() $\lambda _{k,0}$ against the contact-angle
$\lambda _{k,0}$ against the contact-angle ![]() $\alpha$ for
$\alpha$ for ![]() $\chi =0$. This is the most stable situation. For the limiting case of the hemispherical drop (
$\chi =0$. This is the most stable situation. For the limiting case of the hemispherical drop (![]() $\alpha =90^{\circ }$), the pinned modes are precisely the Rayleigh modes (1.1), as expected. The
$\alpha =90^{\circ }$), the pinned modes are precisely the Rayleigh modes (1.1), as expected. The ![]() $[1,0]$ pinned mode has zero frequency and this is related to translational invariance which according to Noether's theorem requires a first integral of motion, as reflected in the zero-frequency motion. Deviations in either
$[1,0]$ pinned mode has zero frequency and this is related to translational invariance which according to Noether's theorem requires a first integral of motion, as reflected in the zero-frequency motion. Deviations in either ![]() $\alpha$ or
$\alpha$ or ![]() $\chi$ break this symmetry and result in non-zero frequency. This mode is a cousin of the ‘walking instability’
$\chi$ break this symmetry and result in non-zero frequency. This mode is a cousin of the ‘walking instability’ ![]() $[1,1]$ mode for the sessile drop (Bostwick & Steen Reference Bostwick and Steen2014). Here we note the pinned (
$[1,1]$ mode for the sessile drop (Bostwick & Steen Reference Bostwick and Steen2014). Here we note the pinned (![]() $\mathcal {P}$) frequencies are always larger than the free (
$\mathcal {P}$) frequencies are always larger than the free (![]() $\mathcal {F}$) frequencies for fixed mode number
$\mathcal {F}$) frequencies for fixed mode number ![]() $[k,0]$. Most modes are stable and exhibit oscillations, with the exception of the
$[k,0]$. Most modes are stable and exhibit oscillations, with the exception of the ![]() $[1,0]$ mode which is unstable for all
$[1,0]$ mode which is unstable for all ![]() $\alpha$ for free disturbances and unstable for super-hemispherical
$\alpha$ for free disturbances and unstable for super-hemispherical ![]() $\alpha >90^{\circ }$ base-states for pinned disturbances. The latter stability limit is related to the pressure turning point in the pressure–volume curve for a pinned sessile drop (Bostwick & Steen Reference Bostwick and Steen2015, figure 1c). Increasing
$\alpha >90^{\circ }$ base-states for pinned disturbances. The latter stability limit is related to the pressure turning point in the pressure–volume curve for a pinned sessile drop (Bostwick & Steen Reference Bostwick and Steen2015, figure 1c). Increasing ![]() $\chi >0$ further destabilizes the
$\chi >0$ further destabilizes the ![]() $[1,0]$ mode, but has little effect on the higher order
$[1,0]$ mode, but has little effect on the higher order ![]() $[k\geqslant 3,0]$ frequencies, as shown in figure 4(b). This is because the
$[k\geqslant 3,0]$ frequencies, as shown in figure 4(b). This is because the ![]() $[1,0]$ mode is primarily responsible for volume change through vertical centre-of-mass motion.
$[1,0]$ mode is primarily responsible for volume change through vertical centre-of-mass motion.

Figure 4. Zonal mode (![]() $l=0$) frequency
$l=0$) frequency ![]() $\lambda$ against (
$\lambda$ against (![]() $a$) contact-angle
$a$) contact-angle ![]() $\alpha$ for
$\alpha$ for ![]() $\chi =0$ and (
$\chi =0$ and (![]() $b$)
$b$) ![]() $\chi$ for
$\chi$ for ![]() $\alpha =110^{\circ }$. Here
$\alpha =110^{\circ }$. Here ![]() $\textrm {Im}[\lambda ]=0$ except for the
$\textrm {Im}[\lambda ]=0$ except for the ![]() $[1,0]$ free mode and
$[1,0]$ free mode and ![]() $[1,0]$ pinned mode for
$[1,0]$ pinned mode for ![]() $\alpha >90^{\circ }$.
$\alpha >90^{\circ }$.
The instability growth rate ![]() $-\textrm {Im}[\lambda _{1,0}]$ for the
$-\textrm {Im}[\lambda _{1,0}]$ for the ![]() $[1,0]$ mode increases monotonically with
$[1,0]$ mode increases monotonically with ![]() $\chi$, as shown in figure 5(a). The free
$\chi$, as shown in figure 5(a). The free ![]() $[1,0]$ mode is unstable for all (
$[1,0]$ mode is unstable for all (![]() $\alpha,\chi$), whereas for the pinned
$\alpha,\chi$), whereas for the pinned ![]() $[1,0]$ mode there is a more complicated dependence. For fixed
$[1,0]$ mode there is a more complicated dependence. For fixed ![]() $\chi$, there is a range of unstable
$\chi$, there is a range of unstable ![]() $\alpha$, as shown in figure 5(b). Here the instability growth rate increases as one moves away from the stability limit
$\alpha$, as shown in figure 5(b). Here the instability growth rate increases as one moves away from the stability limit ![]() $\textrm {Im}[\lambda ]=0$ into the unstable region. Figure 5(c) plots the stability diagram for the pinned
$\textrm {Im}[\lambda ]=0$ into the unstable region. Figure 5(c) plots the stability diagram for the pinned ![]() $[1,0]$ mode in the
$[1,0]$ mode in the ![]() $\chi \times \alpha$ parameter space.
$\chi \times \alpha$ parameter space.

Figure 5. The unstable ![]() $[1,0]$ mode. Instability growth rate
$[1,0]$ mode. Instability growth rate ![]() $-\textrm {Im}[\lambda ]$ against (
$-\textrm {Im}[\lambda ]$ against (![]() $a$)
$a$) ![]() $\chi$ for
$\chi$ for ![]() $\alpha =110^{\circ }$ and (
$\alpha =110^{\circ }$ and (![]() $b$) contact-angle
$b$) contact-angle ![]() $\alpha$ for
$\alpha$ for ![]() $\chi =0.1,1$. (
$\chi =0.1,1$. (![]() $c$) Stability diagram in the
$c$) Stability diagram in the ![]() $\chi \times \alpha$ parameter space separates stable from unstable regions for pinned drops with instability shape inset. Note that free drops are unstable for all
$\chi \times \alpha$ parameter space separates stable from unstable regions for pinned drops with instability shape inset. Note that free drops are unstable for all ![]() $(\alpha,\chi )$.
$(\alpha,\chi )$.
3.2. Rocking  $\ell =1$ modes
$\ell =1$ modes
Figure 6(a) plots the rocking mode ![]() $\ell =1$ frequencies against contact-angle
$\ell =1$ frequencies against contact-angle ![]() $\alpha$, all of which decrease monotonically with increasing
$\alpha$, all of which decrease monotonically with increasing ![]() $\alpha$. Recall that all
$\alpha$. Recall that all ![]() $\ell \neq 0$ modes are independent of
$\ell \neq 0$ modes are independent of ![]() $\chi$. The
$\chi$. The ![]() $[2,1]$ free mode exhibits instability to super-hemispherical
$[2,1]$ free mode exhibits instability to super-hemispherical ![]() $\alpha >90^{\circ }$ base-states, as shown in figure 6(b). Figure 6(c) shows the instability mode shape, which correlates with horizontal centre-of-mass motion, similar to the
$\alpha >90^{\circ }$ base-states, as shown in figure 6(b). Figure 6(c) shows the instability mode shape, which correlates with horizontal centre-of-mass motion, similar to the ![]() $[1,1]$ walking instability mode for the sessile drop (Bostwick & Steen Reference Bostwick and Steen2014). The instability mechanism is similar and results from a decrease in both liquid/gas and liquid/solid interfacial areas (equivalently energies), giving rise to this motion.
$[1,1]$ walking instability mode for the sessile drop (Bostwick & Steen Reference Bostwick and Steen2014). The instability mechanism is similar and results from a decrease in both liquid/gas and liquid/solid interfacial areas (equivalently energies), giving rise to this motion.

Figure 6. Rocking modes (![]() $l=1$). (
$l=1$). (![]() $a$) Frequency
$a$) Frequency ![]() $\lambda$ against contact-angle
$\lambda$ against contact-angle ![]() $\alpha$ contrasting pinned and free modes, with
$\alpha$ contrasting pinned and free modes, with ![]() $\textrm {Im}[\lambda ]=0$ except for the unstable
$\textrm {Im}[\lambda ]=0$ except for the unstable ![]() $[2,1]$ free mode with
$[2,1]$ free mode with ![]() $\alpha >90^{\circ }$. (
$\alpha >90^{\circ }$. (![]() $b$) Instability growth rate
$b$) Instability growth rate ![]() $-\textrm {Im}[\lambda ]$ for the
$-\textrm {Im}[\lambda ]$ for the ![]() $[2,1]$ free mode against contact-angle
$[2,1]$ free mode against contact-angle ![]() $\alpha$ and (
$\alpha$ and (![]() $c$) typical unstable mode shape for
$c$) typical unstable mode shape for ![]() $\alpha =110^{\circ }$.
$\alpha =110^{\circ }$.
3.3. Azimuthal  $\ell \neq 0,1$ modes
$\ell \neq 0,1$ modes
Figures 7 and 8 show how the azimuthal modes break the hemispherical base-state degeneracy for pinned and free disturbances, respectively. Recall for ![]() $\ell \neq 0$, there is no volume exchange between the drop and reservoir, i.e. no effect of
$\ell \neq 0$, there is no volume exchange between the drop and reservoir, i.e. no effect of ![]() $\chi$ on the frequencies. Pinned drops respect the Rayleigh mode degeneracy for hemispherical
$\chi$ on the frequencies. Pinned drops respect the Rayleigh mode degeneracy for hemispherical ![]() $\alpha =90^{\circ }$ base-state, as required by symmetry extension. The pinned mode degeneracy is broken for
$\alpha =90^{\circ }$ base-state, as required by symmetry extension. The pinned mode degeneracy is broken for ![]() $\alpha \neq 90^{\circ }$. Here for fixed polar mode number
$\alpha \neq 90^{\circ }$. Here for fixed polar mode number ![]() $k$, frequencies split lower (higher) for sub-hemispherical
$k$, frequencies split lower (higher) for sub-hemispherical ![]() $\alpha <90^{\circ }$ (super-hemispherical
$\alpha <90^{\circ }$ (super-hemispherical ![]() $\alpha >90^{\circ }$) base-states with increasing azimuthal mode number
$\alpha >90^{\circ }$) base-states with increasing azimuthal mode number ![]() $\ell$. The degeneracy centre for the free modes shifts to lower
$\ell$. The degeneracy centre for the free modes shifts to lower ![]() $\alpha$ which also depends upon
$\alpha$ which also depends upon ![]() $k$, as shown in figure 8. For all modes, pinned and free, the frequency decreases monotonically with increasing
$k$, as shown in figure 8. For all modes, pinned and free, the frequency decreases monotonically with increasing ![]() $\alpha$ because of the higher inertia (volume) which biases towards lower frequency. The slope of the respective curve for fixed
$\alpha$ because of the higher inertia (volume) which biases towards lower frequency. The slope of the respective curve for fixed ![]() $k$ decreases with increasing
$k$ decreases with increasing ![]() $\ell$ and this is related to the predominantly horizontal motions for such modes which are less impacted by base-state volume. This phenomenon is discussed in more detail in Bostwick & Steen (Reference Bostwick and Steen2014, § 7.3).
$\ell$ and this is related to the predominantly horizontal motions for such modes which are less impacted by base-state volume. This phenomenon is discussed in more detail in Bostwick & Steen (Reference Bostwick and Steen2014, § 7.3).

Figure 7. Oscillation frequency ![]() $\lambda$ for the pinned modes against contact-angle
$\lambda$ for the pinned modes against contact-angle ![]() $\alpha$, as it depends upon azimuthal mode number
$\alpha$, as it depends upon azimuthal mode number ![]() $\ell$, for polar mode number
$\ell$, for polar mode number ![]() $(a)$
$(a)$ ![]() $k=3$, (
$k=3$, (![]() $b$)
$b$) ![]() $k=4$, (
$k=4$, (![]() $c$)
$c$) ![]() $k=5$, (
$k=5$, (![]() $d$)
$d$) ![]() $k=6$, (
$k=6$, (![]() $e$)
$e$) ![]() $k=7$ and (
$k=7$ and (![]() $f$)
$f$) ![]() $k=8$. Here
$k=8$. Here ![]() $\chi =0$.
$\chi =0$.

Figure 8. Oscillation frequency ![]() $\lambda$ for the free modes against contact-angle
$\lambda$ for the free modes against contact-angle ![]() $\alpha$, as it depends upon azimuthal mode number
$\alpha$, as it depends upon azimuthal mode number ![]() $\ell$, for polar mode number
$\ell$, for polar mode number ![]() $(a)$
$(a)$ ![]() $k=3$, (
$k=3$, (![]() $b$)
$b$) ![]() $k=4$, (
$k=4$, (![]() $c$)
$c$) ![]() $k=5$, (
$k=5$, (![]() $d$)
$d$) ![]() $k=6$, (
$k=6$, (![]() $e$)
$e$) ![]() $k=7$ and (
$k=7$ and (![]() $f$)
$f$) ![]() $k=8$. Here
$k=8$. Here ![]() $\chi =0$.
$\chi =0$.
4. Concluding remarks
In this work, we have computed the frequency spectrum for the pressure modes of the sessile drop connected to a fluid reservoir, as they depend upon the contact-angle ![]() $\alpha$ and an empirical parameter
$\alpha$ and an empirical parameter ![]() $\chi$ relating the reservoir pressure to volume exchanged. The motions are characterized by the mode number pair
$\chi$ relating the reservoir pressure to volume exchanged. The motions are characterized by the mode number pair ![]() $[k,\ell ]$ and are related to the Rayleigh drop modes through odd symmetry extension with
$[k,\ell ]$ and are related to the Rayleigh drop modes through odd symmetry extension with ![]() $k+\ell =\mathbb {Z}^{+}_{odd}$ required to prescribe a non-trivial flux across the drop/reservoir boundary. Prior work on sessile-drop oscillations on a rigid substrate have predicted the
$k+\ell =\mathbb {Z}^{+}_{odd}$ required to prescribe a non-trivial flux across the drop/reservoir boundary. Prior work on sessile-drop oscillations on a rigid substrate have predicted the ![]() $k+\ell =\mathbb {Z}^{+}_{even}$ modes related to the Rayleigh drop modes through even symmetry extension, as required by the no-penetration condition on the solid substrate (Bostwick & Steen Reference Bostwick and Steen2014). When combined, these two results provide a comprehensive symmetry decomposition of the Rayleigh drop modes with relationship to sessile-drop motions.
$k+\ell =\mathbb {Z}^{+}_{even}$ modes related to the Rayleigh drop modes through even symmetry extension, as required by the no-penetration condition on the solid substrate (Bostwick & Steen Reference Bostwick and Steen2014). When combined, these two results provide a comprehensive symmetry decomposition of the Rayleigh drop modes with relationship to sessile-drop motions.
We note that our analysis was restricted to inviscid fluids and flat substrates. Viscous effects can be expected to enter this problem through the Ohnesorge number ![]() ${Oh}\equiv \mu /\sqrt {\varrho \sigma R}$ with
${Oh}\equiv \mu /\sqrt {\varrho \sigma R}$ with ![]() $\mu$ the fluid viscosity. For millimetre-sized water drops,
$\mu$ the fluid viscosity. For millimetre-sized water drops, ![]() ${Oh}\approx 0.002$ and the effect of viscosity on the frequency is negligible. In inkjet printing, typical nozzle diameters are
${Oh}\approx 0.002$ and the effect of viscosity on the frequency is negligible. In inkjet printing, typical nozzle diameters are ![]() $10\unicode{x2013}100\ \mathrm {\mu }{\rm m}$ corresponding to
$10\unicode{x2013}100\ \mathrm {\mu }{\rm m}$ corresponding to ![]() ${Oh}\approx 0.01\unicode{x2013}0.03$ implying a stronger viscous effect. Our prior work on forced oscillations of sessile drops suggests that this range of
${Oh}\approx 0.01\unicode{x2013}0.03$ implying a stronger viscous effect. Our prior work on forced oscillations of sessile drops suggests that this range of ![]() ${Oh}$ would still correspond to underdamped oscillations with minimal effect on the frequency, at least for the lower order modes (Bostwick & Steen Reference Bostwick and Steen2016). Lastly, we study the case of a sessile drop on a flat substrate, which differs from other prior works including the spherical bowl (concave) support of Strani & Sabetta (Reference Strani and Sabetta1984). Future studies could address the role of substrate curvature and viscosity.
${Oh}$ would still correspond to underdamped oscillations with minimal effect on the frequency, at least for the lower order modes (Bostwick & Steen Reference Bostwick and Steen2016). Lastly, we study the case of a sessile drop on a flat substrate, which differs from other prior works including the spherical bowl (concave) support of Strani & Sabetta (Reference Strani and Sabetta1984). Future studies could address the role of substrate curvature and viscosity.
The majority of motions predicted here are oscillatory, with the exception of the ![]() $[1,0]$ and
$[1,0]$ and ![]() $[2,1]$ modes, each of which exhibits instability over a specific range of contact-angles that are related to the CL boundary conditions, pinned or free. The axisymmetric
$[2,1]$ modes, each of which exhibits instability over a specific range of contact-angles that are related to the CL boundary conditions, pinned or free. The axisymmetric ![]() $[1,0]$ mode is related to vertical centre-of-mass motion and the drop pinch-off seen in inkjet processes. We note the recent observation of non-axisymmetric effects in the inkjet printing process (Van Der Meulen et al. Reference Van Der Meulen, Reinten, Wijshoff, Versluis, Lohse and Steen2020). This opens up exciting possibilities for spatially resolved printing involving the pinch-off of multiple primary drops from a single print head and requiring control of surface pattern formation that precedes atomization (Vukasinovic, Smith & Glezer Reference Vukasinovic, Smith and Glezer2007). Alternative methods of surface patterning utilize thin films (Deblais et al. Reference Deblais, Harich, Colin and Kellay2016). Our simple lumped-parameter model of the drop/reservoir interactions does not predict such instabilities, as could be expected, but our model could be extended to account for more complex pressure interactions between the drop and fluid reservoir that could potentially lead to the prediction of these asymmetric instabilities. Lastly, we mention that for the engineering application of reliably generating surface patterns that it may be more computationally tractable to utilize reservoir computing (Fernando & Sojakka Reference Fernando and Sojakka2003) than our analytical-based method, which is focused on the fundamental physics.
$[1,0]$ mode is related to vertical centre-of-mass motion and the drop pinch-off seen in inkjet processes. We note the recent observation of non-axisymmetric effects in the inkjet printing process (Van Der Meulen et al. Reference Van Der Meulen, Reinten, Wijshoff, Versluis, Lohse and Steen2020). This opens up exciting possibilities for spatially resolved printing involving the pinch-off of multiple primary drops from a single print head and requiring control of surface pattern formation that precedes atomization (Vukasinovic, Smith & Glezer Reference Vukasinovic, Smith and Glezer2007). Alternative methods of surface patterning utilize thin films (Deblais et al. Reference Deblais, Harich, Colin and Kellay2016). Our simple lumped-parameter model of the drop/reservoir interactions does not predict such instabilities, as could be expected, but our model could be extended to account for more complex pressure interactions between the drop and fluid reservoir that could potentially lead to the prediction of these asymmetric instabilities. Lastly, we mention that for the engineering application of reliably generating surface patterns that it may be more computationally tractable to utilize reservoir computing (Fernando & Sojakka Reference Fernando and Sojakka2003) than our analytical-based method, which is focused on the fundamental physics.
Funding
J.B.B. acknowledges support from NSF Grant CMMI-1935590.
Declaration of interests
The authors report no conflict of interest.