Published online by Cambridge University Press: 09 January 2015
High-Reynolds number gravity currents (GC) in a horizontal channel with circular/semicircular side walls are investigated by comparing experimental data and shallow-water (SW) theoretical results. We focus attention on a Boussinesq system (salt water in fresh water): the denser fluid, occupying part of the depth or the full depth of the ambient fluid which fills the remaining part of the channel, is initially at rest in a lock separated by a gate from the downstream channel. Upon the rapid removal of the gate (‘dam break’), the denser ‘current’ begins propagating into the downstream channel, while a significant adjustment motion propagates upstream in the lock as a bore or rarefaction wave. Using an experimental channel provided by a tube of 19 cm diameter and up to 615 cm length, which could be filled to various levels, we investigated both full-depth and part-depth releases, considered the various stages of inertial-buoyancy propagation (in particular, the initial ‘slumping’ with constant speed, and the transition to the late self-similar propagation with time to the power  $3/4$), and detected the transition to the viscous-buoyancy regime. A first series of tests is focused on the motion in the lock while a second series of tests is focused on the evolution of the downstream current. The speed of propagation of the current in the slumping stage is overpredicted by the theory, by about the same amount (typically 15 %) as observed in the classical flat bottom case. The length of transition to viscous regime turns out to be
$3/4$), and detected the transition to the viscous-buoyancy regime. A first series of tests is focused on the motion in the lock while a second series of tests is focused on the evolution of the downstream current. The speed of propagation of the current in the slumping stage is overpredicted by the theory, by about the same amount (typically 15 %) as observed in the classical flat bottom case. The length of transition to viscous regime turns out to be  ${\sim}[\mathit{Re}_{0}(h_{0}/x_{0})]^{{\it\alpha}}$ (
${\sim}[\mathit{Re}_{0}(h_{0}/x_{0})]^{{\it\alpha}}$ ( $\mathit{Re}_{0}=(g^{\prime }h_{0})^{1/2}h_{0}/{\it\nu}_{c}$ is the initial Reynolds number,
$\mathit{Re}_{0}=(g^{\prime }h_{0})^{1/2}h_{0}/{\it\nu}_{c}$ is the initial Reynolds number, 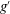 $g^{\prime }$ is the reduced gravity,
$g^{\prime }$ is the reduced gravity,  ${\it\nu}_{c}$ is the kinematic viscosity of the denser fluid,
${\it\nu}_{c}$ is the kinematic viscosity of the denser fluid,  $h_{0}$ and
$h_{0}$ and  $x_{0}$ are the height of the denser current and the length of the lock, respectively), with the theoretical
$x_{0}$ are the height of the denser current and the length of the lock, respectively), with the theoretical  ${\it\alpha}=3/8$ and experimental
${\it\alpha}=3/8$ and experimental  ${\it\alpha}\approx 0.27$.
${\it\alpha}\approx 0.27$.