Published online by Cambridge University Press: 31 July 2014
We investigate the motion of high-Reynolds-number gravity currents (GCs) in a horizontal channel of V-shaped cross-section combining lock-exchange experiments and a theoretical model. While all previously published experiments in V-shaped channels were performed with the special configuration of the full-depth lock, we present the first part-depth experiment results. A fixed volume of saline, that was initially of length 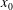 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x_0$ and height
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}x_0$ and height 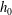 $h_0$ in a lock and embedded in water of height
$h_0$ in a lock and embedded in water of height  $H_0$ in a long tank, was released from rest and the propagation was recorded over a distance of typically
$H_0$ in a long tank, was released from rest and the propagation was recorded over a distance of typically 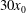 $ 30 x_0$ . In all of the tested cases the current displays a slumping stage of constant speed
$ 30 x_0$ . In all of the tested cases the current displays a slumping stage of constant speed 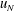 $u_N$ over a significant distance
$u_N$ over a significant distance 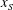 $x_S$ , followed by a self-similar stage up to the distance
$x_S$ , followed by a self-similar stage up to the distance 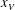 $x_V$ , where transition to the viscous regime occurs. The new data and insights of this study elucidate the influence of the height ratio
$x_V$ , where transition to the viscous regime occurs. The new data and insights of this study elucidate the influence of the height ratio 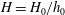 $H = H_0/h_0$ and of the initial Reynolds number
$H = H_0/h_0$ and of the initial Reynolds number 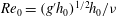 ${\mathit{Re}}_0 = (g^{\prime }h_0)^{{{1/2}}} h_0/ \nu $ , on the motion of the triangular GC;
${\mathit{Re}}_0 = (g^{\prime }h_0)^{{{1/2}}} h_0/ \nu $ , on the motion of the triangular GC; 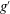 $g^{\prime }$ and
$g^{\prime }$ and  $\nu $ are the reduced gravity and kinematic viscosity coefficient, respectively. We demonstrate that the speed of propagation
$\nu $ are the reduced gravity and kinematic viscosity coefficient, respectively. We demonstrate that the speed of propagation 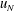 $u_N$ scaled with
$u_N$ scaled with 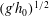 $(g^{\prime } h_0)^{{{1/2}}}$ increases with
$(g^{\prime } h_0)^{{{1/2}}}$ increases with 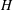 $H$ , while
$H$ , while 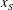 $x_S$ decreases with
$x_S$ decreases with  $H$ , and
$H$ , and 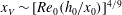 $x_V \sim [{\mathit{Re}}_0(h_0/x_0)]^{{4/9}}$ . The initial propagation in the triangle is 50 % more rapid than in a standard flat-bottom channel under similar conditions. Comparisons with theoretical predictions show good qualitative agreements and fair quantitative agreement; the major discrepancy is an overpredicted
$x_V \sim [{\mathit{Re}}_0(h_0/x_0)]^{{4/9}}$ . The initial propagation in the triangle is 50 % more rapid than in a standard flat-bottom channel under similar conditions. Comparisons with theoretical predictions show good qualitative agreements and fair quantitative agreement; the major discrepancy is an overpredicted 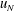 $u_N$ , similar to that observed in the standard flat bottom case.
$u_N$ , similar to that observed in the standard flat bottom case.