Hostname: page-component-66644f4456-q629f Total loading time: 0 Render date: 2025-02-12T12:46:28.879Z Has data issue: true hasContentIssue false
  • English
  • Français

Proper orthogonal decomposition analysis and modelling of large-scale flow reorientations in a cubic Rayleigh–Bénard cell

Published online by Cambridge University Press:  24 October 2019

Laurent Soucasse Open the ORCID record for Laurent Soucasse [Opens in a new window] ,
Bérengère Podvin Open the ORCID record for Bérengère Podvin [Opens in a new window] ,
Philippe Rivière  and
Anouar Soufiani
Laurent Soucasse*
Affiliation:
Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 8-10 rue Joliot Curie, 91192 Gif-sur-Yvette, France
Bérengère Podvin
Affiliation:
LIMSI, CNRS, Université Paris-Saclay, Bât 507, rue du Belvédère, Campus Universitaire, 91405 Orsay, France
Philippe Rivière
Affiliation:
Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 8-10 rue Joliot Curie, 91192 Gif-sur-Yvette, France
Anouar Soufiani
Affiliation:
Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 8-10 rue Joliot Curie, 91192 Gif-sur-Yvette, France
*
†Email address for correspondence: laurent.soucasse@centralesupelec.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the large-scale flow reorientations of Rayleigh–Bénard convection in a cubic cell using proper orthogonal decomposition (POD) analysis and modelling. A direct numerical simulation is performed for air at a Rayleigh number of 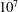$10^{7}$ and shows that the flow is characterized by four quasi-stable states, corresponding to a large-scale circulation lying in one of the two diagonal planes of the cube with a clockwise or anticlockwise motion, with occasional brief reorientations. Proper orthogonal decomposition is applied to the joint velocity and temperature fields of an enriched database which captures the statistical symmetries of the flow. We found that each quasi-stable state consists of a superposition of four spatial modes representing three types of structures: (i) a mean-flow mode consisting of two stacked counter-rotating torus-like structures; (ii) two large-scale two-dimensional rolls (pair of degenerated modes) which form large-scale diagonal rolls when combined together; and (iii) an eight-roll mode that transports fluid from one corner to the other and strengthens the circulation along the diagonal. In addition, we identified three other modes that play a role in the reorientation process: two boundary-layer modes (pair of degenerated modes) that connect the core region with the horizontal boundary layers and one mode associated with corner rolls. The symmetries of the different POD modes are discussed, as well as their temporal dynamics. A description of the reorientation process in terms of POD modes is provided and compared with other modal approaches available in the literature. Finally, Galerkin projection is used to derive a POD-based reduced-order model. Unresolved modes are accounted for in the model by an extra dissipation term and the addition of noise. A seven-mode model is able to reproduce the low-frequency dynamics of the large-scale reorientations as well as the high-frequency dynamics associated with the large-scale circulation rotation. Linear stability analysis and sensitivity analysis confirm the role of the boundary-layer modes and the corner-rolls mode in the reorientation process.

JFM classification

Nonlinear Dynamical Systems: Low-dimensional models
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 23 - 50
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bai, K., Ji, D. & Brown, E. 2016 Ability of a low-dimensional model to predict geometry-dependent dynamics of large-scale coherent structures in turbulence. Phys. Rev. E 93, 023117.Google Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependece of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.Google Scholar
Benzi, R. & Verzicco, R. 2008 Numerical simulations of flow reversal in Rayleigh–Bénard convection. Europhys. Lett. 81 (6), 64008.Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.Google Scholar
Brown, E. & Ahlers, G. 2007 Large-scale circulation model for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 134501.Google Scholar
Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Reorientation of the large-scale circulation in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 95, 084503.Google Scholar
Castillo-Castellanos, A., Sergent, A. & Rossi, M. 2016 Reversal cycle in square Rayleigh–Bénard cells in turbulent regime. J. Fluid Mech. 808, 614–640.Google Scholar
Chandra, M. & Verma, M. K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83, 067303.Google Scholar
Chandra, M. & Verma, M. K. 2013 Flow reversals in turbulent convection via vortex reconnections. Phys. Rev. Lett. 110, 114503.Google Scholar
Foroozani, N., Niemela, J. J., Armenio, V. & Sreenivasan, K. R. 2017 Reorientations of the large-scale flow in turbulent convection in a cube. Phys. Rev. E 95, 033107.Google Scholar
Giannakis, D., Kolchinskaya, A., Krasnov, D. & Schumacher, J. 2018 Koopman analysis of the long-term evolution in a turbulent convection cell. J. Fluid Mech. 847, 735–767.Google Scholar
Holmes, P., Lumley, J. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams and convergence zones in turbulent flows. In Center for Turbulence Research, Proceedings of the Summer Program.Google Scholar
Mishra, P. K., Verman, A. K. & ESwaran, V. 2011 Dynamics of reorientations and reversals of large-scale flow in Rayleigh–Bénard convection. J. Fluid Mech. 668, 480–499.Google Scholar
Moin, P. & Moser, R. D. 1989 Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 200, 471–509.Google Scholar
Podvin, B. & Le Quéré, P. 2001 Low-order models for the flow in a differentially heated cavity. Phys. Fluids 13 (11), 3204–3214.Google Scholar
Podvin, B. & Sergent, A. 2012 Proper orthogonal decomposition investigation of turbulent Rayleigh–Bénard convection in a rectangular cavity. Phys. Fluids 24, 105106.Google Scholar
Podvin, B. & Sergent, A. 2015 A large-scale investigation of wind reversal in a square Rayleigh–Bénard cell. J. Fluid Mech. 766, 172–201.Google Scholar
Podvin, B. & Sergent, A. 2017 Precursor for wind reversal in a square Rayleigh–Bénard cell. Phys. Rev. E 95, 013112.Google Scholar
Puigjaner, D., Herrero, J., Simo, C. & Giralt, F. 2008 Bifurcation analysis of steady Rayleigh–Bénard convection in a cubical cavity with conducting sidewalls. J. Fluid Mech. 598, 393–427.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamic of coherent structures. Part I: coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Sreenivasan, K. R., Bershadski, A. & Niemela, J. J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65, 056306.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.Google Scholar
Vasiliev, A., Frick, P., Kumar, A., Stepanov, R., Sukhanovskii, A. & Verma, M. K. 2019 Transient flows and reorientations of large-scale convection in a cubic cell. Intl Commun. Heat Mass Transfer 108, 104319.Google Scholar
Vasiliev, A., Sukhanovskii, A., Frick, P., Budnikov, A., Fomichev, V., Bolshukhin, M. & Romanov, R. 2016 High Rayleigh number convection in a cubic cell with adiabatic sidewalls. Intl J. Heat Mass Transfer 102, 201–212.Google Scholar
Verdoold, J., Tummers, M. J. & Hanjalić, K. 2009 Prime modes of fluid circulation in large-aspect-ratio turbulent Rayleigh–Bénard convection. Phys. Rev. E 80, 037301.Google Scholar
Xin, S., Chergui, J. & Le Quéré, P. 2010 3D spectral parallel multi-domain computing for natural convection flows. In Parallel Computational Fluid Dynamics 2008 (ed. Tromeur-Dervout, D., Brenner, G., Emerson, D. R. & Erhel, J.), Lecture Notes in Computational Science and Engineering, vol. 74, pp. 163–171. Springer.Google Scholar
Xin, S. & Le Quéré, P. 2002 An extended Chebyshev pseudo-spectral benchmark for the 8:1 differentially heated cavity. Intl J. Heat Mass Transfer 40, 981–998.Google Scholar
Supplementary material: File

Soucasse et al. supplementary material

Soucasse et al. supplementary material

Download Soucasse et al. supplementary material(File)
File 136.7 KB