Article contents
Radius ratio dependency of the instability of fully compressible convection in rapidly rotating spherical shells
Published online by Cambridge University Press: 02 September 2021
Abstract
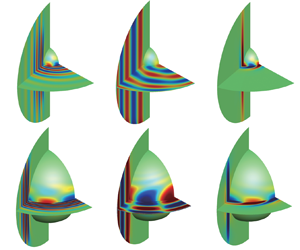
Based on the fully compressible Navier–Stokes equations, the linear stability of thermal convection in rapidly rotating spherical shells of various radius ratios  $\eta$ is studied for a wide range of Taylor number
$\eta$ is studied for a wide range of Taylor number  $Ta$, Prandtl number
$Ta$, Prandtl number  $Pr$ and the number of density scale height
$Pr$ and the number of density scale height  $N_\rho$. Besides the classical inertial mode and columnar mode, which are widely studied by the Boussinesq approximation and anelastic approximation, the quasi-geostrophic compressible mode is also identified in a wide range of
$N_\rho$. Besides the classical inertial mode and columnar mode, which are widely studied by the Boussinesq approximation and anelastic approximation, the quasi-geostrophic compressible mode is also identified in a wide range of  $N_\rho$ and
$N_\rho$ and  $Pr$ for all
$Pr$ for all  $\eta$ considered, and this mode mainly occurs in the convection with relatively small
$\eta$ considered, and this mode mainly occurs in the convection with relatively small  $Pr$ and large
$Pr$ and large  $N_\rho$. The instability processes are classified into five categories. In general, for the specified wavenumber
$N_\rho$. The instability processes are classified into five categories. In general, for the specified wavenumber  $m$, the parameter space (
$m$, the parameter space ( $Pr, N_\rho$) of the fifth category, in which the base state loses stability via the quasi-geostrophic compressible mode and remains unstable, shrinks as
$Pr, N_\rho$) of the fifth category, in which the base state loses stability via the quasi-geostrophic compressible mode and remains unstable, shrinks as  $\eta$ increases. The asymptotic scaling behaviours of the critical Rayleigh numbers
$\eta$ increases. The asymptotic scaling behaviours of the critical Rayleigh numbers  $Ra_c$ and corresponding wavenumbers
$Ra_c$ and corresponding wavenumbers  $m_c$ to
$m_c$ to  $Ta$ are found at different
$Ta$ are found at different  $\eta$ for the same instability mode. As
$\eta$ for the same instability mode. As  $\eta$ increases, the flow stability is strengthened. Furthermore, the linearized perturbation equations and Reynolds–Orr equation are employed to quantitatively analyse the mechanical mechanisms and flow instability mechanisms of different modes. In the quasi-geostrophic compressible mode, the time-derivative term of disturbance density in the continuity equation and the diffusion term of disturbance temperature in the energy equation are found to be critical, while in the columnar and inertial modes, they can generally be ignored. Because the time-derivative term of the disturbance density in the continuity equation cannot be ignored, the anelastic approximation fails to capture the instability mode in the small-
$\eta$ increases, the flow stability is strengthened. Furthermore, the linearized perturbation equations and Reynolds–Orr equation are employed to quantitatively analyse the mechanical mechanisms and flow instability mechanisms of different modes. In the quasi-geostrophic compressible mode, the time-derivative term of disturbance density in the continuity equation and the diffusion term of disturbance temperature in the energy equation are found to be critical, while in the columnar and inertial modes, they can generally be ignored. Because the time-derivative term of the disturbance density in the continuity equation cannot be ignored, the anelastic approximation fails to capture the instability mode in the small- $Pr$ and large-
$Pr$ and large- $N_\rho$ system, where convection onset is dominated by the quasi-geostrophic compressible mode. However, all the modes are primarily governed by the balance between the Coriolis force and the pressure gradient, based on the momentum equation. Physically, the most important difference between the quasi-geostrophic compressible mode and the columnar mode is the role played by the disturbance pressure. The disturbance pressure performs negative work for the former mode, which appears to stabilize the flow, while it destabilizes the flow for the latter mode. As
$N_\rho$ system, where convection onset is dominated by the quasi-geostrophic compressible mode. However, all the modes are primarily governed by the balance between the Coriolis force and the pressure gradient, based on the momentum equation. Physically, the most important difference between the quasi-geostrophic compressible mode and the columnar mode is the role played by the disturbance pressure. The disturbance pressure performs negative work for the former mode, which appears to stabilize the flow, while it destabilizes the flow for the latter mode. As  $\eta$ increases, in the former mode the relative work performed by the disturbance pressure increases and in the latter mode decreases.
$\eta$ increases, in the former mode the relative work performed by the disturbance pressure increases and in the latter mode decreases.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 1
- Cited by


