Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T06:41:32.309Z Has data issue: false hasContentIssue false
  • English
  • Français

Range of validity of an extended WKB theory for atmospheric gravity waves: one-dimensional and two-dimensional case

Published online by Cambridge University Press:  19 July 2013

Felix Rieper ,
U. Achatz  and
R. Klein
Felix Rieper*
Affiliation:
Institut für Atmosphäre und Umwelt, Goethe Universität, D-60438 Frankfurt am Main, Germany
U. Achatz
Affiliation:
Institut für Atmosphäre und Umwelt, Goethe Universität, D-60438 Frankfurt am Main, Germany
R. Klein
Affiliation:
Institut für Mathematik, Freie Universität, 14195 Berlin, Germany
*
†Present address: Deutscher Wetterdienst, 63067 Offenbach, Germany. Email address for correspondence: felix.rieper@dwd.de
Get access Rights & Permissions [Opens in a new window]

Abstract

A computational model of the pseudo-incompressible equations is used to probe the range of validity of an extended Wentzel–Kramers–Brillouin theory (XWKB), previously derived through a distinguished limit of a multiple-scale asymptotic analysis of the Euler or pseudo-incompressible equations of motion, for gravity-wave packets at large amplitudes. The governing parameter of this analysis had been the scale-separation ratio $\varepsilon $ between the gravity wave and both the large-scale potential-temperature stratification and the large-scale wave-induced mean flow. A novel feature of the theory had been the non-resonant forcing of higher harmonics of an initial wave packet, predominantly by the large-scale gradients in the gravity-wave fluxes. In the test cases considered a gravity-wave packet is propagating upwards in a uniformly stratified atmosphere. Large-scale winds are induced by the wave packet, and possibly exert a feedback on the latter. In the limit 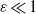$\varepsilon \ll 1$ all predictions of the theory can be validated. The larger $\varepsilon $ is the more the transfer of wave energy to the mean flow is underestimated by the theory. The numerical results quantify this behaviour but also show that, qualitatively, XWKB remains valid even when the gravity-wave wavelength approaches the spatial scale of the wave-packet amplitude. This includes the prevalence of first and second harmonics and the smallness of harmonics with wave number higher than two. Furthermore, XWKB predicts for the vertical momentum balance an additional leading-order buoyancy term in Euler and pseudo-incompressible theory, compared with the anelastic theory. Numerical tests show that this term is relatively large with up to 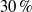$30\hspace{0.167em} \% $ of the total balance. The practical relevance of this deviation remains to be assessed in future work.

JFM classification

Geophysical and Geological Flows: Atmospheric flows Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Stratified flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 330 - 363
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Achatz, U. 2005 On the role of optimal perturbations in the instability of monochromatic gravity waves. Phys. Fluids 17, 094107.Google Scholar
Achatz, U. 2007 Modal and nonmodal perturbations of monochromatic high-frequency gravity waves: primary nonlinear dynamics. J. Atmos. Sci. 64, 1977–1994.Google Scholar
Achatz, U., Klein, R. & Senf, F. 2010 Gravity waves, scale asymptotics, and the pseudo-incompressible equations. J. Fluid Mech. 663, 120–147.Google Scholar
Alexander, M. J. & Dunkerton, T. J. 1999 A spectral parameterization of mean-flow forcing due to breaking gravity waves. J. Atmos. Sci. 56, 4167–4182.Google Scholar
Alexander, M. J., Geller, M., McLandress, C., Polavarapu, S., Preusse, P., Sassi, F., Sato, K., Eckermann, S., Ern, M., Hertzog, A., Kawatani, Y., Pulido, M., Shaw, T. A., Sigmond, M., Vincent, R. & Watanabe, S. 2010 Recent developments in gravity-wave effects in climate models and the global distribution of gravity-wave momentum flux from observations and models. Q. J. R. Meteorol. Soc. 136, 1103–1124.CrossRefGoogle Scholar
Bretherton, F. P. 1966 The propagation of groups of internal gravity waves in a shear flow. Q. J. R. Meteorol. Soc. 92, 466–480.Google Scholar
Caillol, P. & Zeitlin, V. 2000 Kinetic equations and stationary energy spectra of weakly nonlinear internal gravity waves. Dyn. Atmos. Oceans 32 (2), 81–112.Google Scholar
Dosser, H. V. & Sutherland, B. R. 2011 Anelastic internal wave packet evolution and stability. J. Atmos. Sci. 68 (12), 2844–2859.Google Scholar
Dunkerton, T. J. 1981 Wave transience in a compressible atmosphere. Part I: transient internal wave, mean-flow interaction. J. Atmos. Sci. 38 (2), 281–297.Google Scholar
Dunkerton, T. J. 1982 Wave transience in a compressible atmosphere. Part III: the saturation of internal gravity waves in the mesophere. J. Atmos. Sci. 39 (5), 1042–1051.Google Scholar
Dunkerton, T. J. 1984 Inertia–gravity waves in the stratosphere. J. Atmos. Sci. 41 (23), 3396–3404.Google Scholar
Dunkerton, T. J. 1987 Effect of nonlinear instability on gravity-wave momentum transport. J. Atmos. Sci. 44 (21), 3188–3209.Google Scholar
Durran, D. R. 1989 Improving the anelastic approximation. J. Atmos. Sci. 46, 1453–1461.Google Scholar
Durran, D. R. 1999 Numerical Methods for Wave Equations in Geophysical Fluid Dynamics. Springer.Google Scholar
Fritts, D. C. & Alexander, M. J. 2003 Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 41 (1), 1003.Google Scholar
Fritts, D. C., Vadas, S. L., Wan, K. & Werne, J. A. 2006 Mean and variable forcing of the middle atmosphere by gravity waves. J. Atmos. Sol.-Terr. Phys. 68, 247–265.Google Scholar
Grimshaw, R. 1975a Internal gravity waves: critical layer absorption in a rotating fluid. J. Fluid Mech. 70, 287–304.Google Scholar
Grimshaw, R. 1975b Nonlinear internal gravity waves in a rotating fluid. J. Fluid Mech. 71, 497–512.Google Scholar
Hines, C. O. 1997 Doppler spread parameterization of gravity-wave momentum deposition in the middle atmosphere. Part 1. Basic formulation. J. Atmos. Sol.-Terr. Phys. 59, 371–386.Google Scholar
Holton, J. R. 1982 The role of gravity wave induced drag and diffusion in the momentum budget of the mesosphere. J. Atmos. Sci. 39, 791–799.Google Scholar
Kemm, F. 2010 A comparative study of TVD-limiters—well-known limiters and an introduction of new ones. Intl J. Numer. Meth. Fluids 67 (4), 404–440.Google Scholar
Kim, Y.-J., Eckermann, S. D. & Chun, H.-Y. 2003 An overview of the past, present and future of gravity-wave drag parametrization for numerical climate and weather prediction models. Atmos.-Ocean 41, 65–98.Google Scholar
Klein, R. 2009 Asymptotics, structure, and integration of sound-proof atmospheric flow equations. Theor. Comput. Fluid Dyn. 23, 161–195.Google Scholar
Klein, R. 2010 Scale-dependent models for atmospheric flows. Annu. Rev. Fluid Mech. 42, 249–274.Google Scholar
Klein, R. 2011 On the regime of validity of sound-proof model equations for atmospheric flows. ESMWF Workshop on Non-hydrostatic Modelling, 8–10 November 2010.Google Scholar
Lindzen, R. S. 1981 Turbulence and stress owing to gravity wave and tidal breakdown. J. Geophys. Res. 86, 9707–9714.Google Scholar
Lipps, F. & Hemler, R. 1982 A scale analysis of deep moist convection and some related numerical calculations. J. Atmos. Sci. 29, 2192–2210.Google Scholar
Lombard, P. N. & Riley, J. R. 1996 Instability and breakdown of internal gravity waves. I. Linear stability analysis. Phys. Fluids 8, 3271–3287.Google Scholar
Lvov, Y. V., Polzin, K. L. & Yokoyama, N. 2012 Resonant and near-resonant internal wave interactions. J. Phys. Oceanogr. 42 (5), 669–691.Google Scholar
McComas, C. H. & Bretherton, F. P. 1977 Resonant interaction of oceanic internal waves. J. Geophys. Res. 82, 1397–1412.Google Scholar
Medvedev, A. S. & Klaassen, G. P. 1995 Vertical evolution of gravity wave spectra and the parameterization of associated gravity wave drag. J. Geophys. Res. 100, 25841–25853.Google Scholar
Müller, P. 1976 On the diffusion of momentum and mass by internal gravity waves. J. Fluid Mech. 77, 789–823.Google Scholar
Rieper, F., Hickel, S. & Achatz, U. 2013 A conservative integration of the pseudo-incompressible equations with implicit turbulence parameterization. Mon. Weath. Rev. 141, 861–886.Google Scholar
Smolarkiewicz, P. K. & Szmelter, J. 2011 A nonhydrostatic unstructured-mesh soundproof model for simulation of internal gravity waves. Acta Geophys. 59 (6), 1109–1134.Google Scholar
Sutherland, B. R. 2006 Weakly nonlinear internal gravity wavepackets. J. Fluid Mech. 569, 249–258.Google Scholar
Sutherland, B. R. 2010 Internal Gravity Waves. Cambridge University Press.Google Scholar
Toro, E. F. 1999 Riemann Solvers and Numerical Methods for Fluid Dynamics, A Practical Introduction, 2nd edn. Springer.Google Scholar