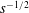1 Introduction
In this paper we consider a steady flow of a rarefied gas induced around a rotating sphere in an unbounded domain. The problem is one of the most fundamental external flow problems in fluid mechanics and in rarefied gas dynamics, whose practical applications can be sought in aerosol sciences and/or in vacuum engineering. In this paper, we revisit this classical problem (Loyalka Reference Loyalka1992) and carry out precise numerical analysis on the basis of the ellipsoidal statistical model of the Boltzmann equation (the ES model) and the Maxwell diffuse–specular boundary condition.
Our motivation for the present study is twofold. The first is related to the Magnus effect in a rarefied gas. That is, when there is a flow over a rotating sphere, the sphere experiences a lift known as the Magnus force (see e.g. Rubinow & Keller Reference Rubinow and Keller1961). Our interest is to understand and clarify the Magnus force acting on a rotating sphere in a slow rarefied gas flow, for which the present analysis plays an important role. This will be treated in a forthcoming paper.
The second motivation on which we will focus in the present paper is based on recent theoretical works (Takata & Taguchi Reference Takata and Taguchi2017; Takata et al.
Reference Takata, Yoshida, Noguchi and Taguchi2016b
) on singular behaviours of macroscopic quantities of rarefied gases (or the moments of the velocity distribution function (VDF)). In rarefied gases, there are two main mechanisms underlying the determination of the behaviour of the gas, namely the molecular (ballistic) transport and collisions (scattering). The effect of the ballistic transport is most highlighted when the gas is in contact with a convex body or boundary. In general, there is a mismatch of the incoming and outgoing data of the unknown (i.e. VDF) on a point on the boundary for the molecular velocity tangent to the boundary, if the boundary is convex or flat. In the case where the boundary is convex, this mismatch, or the discontinuity in VDF, propagates into the gas along the characteristics of the transport equation, causing a singularity in the behaviour of the macroscopic quantities on the boundary (Takata & Taguchi Reference Takata and Taguchi2017). More precisely, the normal derivative of the macroscopic quantities diverges in approaching the boundary with diverging rate
![]() $s^{-1/n}$
, where
$s^{-1/n}$
, where
![]() $s$
is the normal distance from the boundary and
$s$
is the normal distance from the boundary and
![]() $n$
(
$n$
(
![]() $n\geqslant 2$
) is the degree of the dominant terms of the polynomial that locally approximates the boundary.
$n\geqslant 2$
) is the degree of the dominant terms of the polynomial that locally approximates the boundary.
A spherical body is a typical convex body and the flow around a rotating sphere is subject to this singular behaviour. However, this aspect has not been considered in previous studies. A further investigation is still necessary in order to clarify the detailed flow features, including not only the flow velocity and the shear stress, but also the heat flow in the gas. In this paper, we will do this numerically. In particular, we will show that the most rapidly diverging term in the macroscopic quantities is proportional to the magnitude of the jump discontinuity of the VDF on the boundary. This complements previous work (Takata & Taguchi Reference Takata and Taguchi2017) and clearly demonstrates the connection between the jump magnitude and the predicted singularity. The Maxwell boundary condition plays an ingenious role for this purpose. We also note that the present issue has a close connection to the S layer (Sone Reference Sone1973; Sone & Takata Reference Sone and Takata1992) in the situation where the Knudsen number is small.
Incidentally, when the boundary is of a smooth concave shape or plane, the characteristics tangent to the boundary do not enter the gas region. In these cases, a weaker singularity was shown to occur (Takata & Funagane Reference Takata and Funagane2011; Takata & Taguchi Reference Takata and Taguchi2017), that is, the normal derivative of the macroscopic quantities diverges in approaching the boundary with diverging rate
![]() $\ln s$
.
$\ln s$
.
The rest of the paper is organised as follows. After the formulation (§ 2), the reduction of the problem is carried out in § 3. Section 4 summarises analytical results for the cases of large and small Knudsen numbers. Section 5 shows the numerical results, followed by discussions (§ 6). Conclusions are drawn in § 7.
2 Formulation
2.1 Problem and basic assumptions
Let us consider a monatomic ideal gas around a sphere with radius
![]() $L$
rotating about a fixed axis passing through the centre with constant angular velocity
$L$
rotating about a fixed axis passing through the centre with constant angular velocity
![]() $\unicode[STIX]{x1D6FA}^{\ast }$
. We introduce the space rectangular coordinate system
$\unicode[STIX]{x1D6FA}^{\ast }$
. We introduce the space rectangular coordinate system
![]() $Lx_{i}$
(or
$Lx_{i}$
(or
![]() $L\boldsymbol{x}$
) in such a way that the origin is located at the centre of the sphere and that the
$L\boldsymbol{x}$
) in such a way that the origin is located at the centre of the sphere and that the
![]() $x_{1}$
axis is taken to be the axis of revolution of the sphere. At far distance from the sphere, the state of the gas is the resting equilibrium state with density
$x_{1}$
axis is taken to be the axis of revolution of the sphere. At far distance from the sphere, the state of the gas is the resting equilibrium state with density
![]() $\unicode[STIX]{x1D70C}_{\infty }$
and temperature
$\unicode[STIX]{x1D70C}_{\infty }$
and temperature
![]() $T_{\infty }$
. The (uniform) temperature of the sphere is supposed to be the same as that of the gas at infinity. We investigate the steady behaviour of the gas induced around the sphere, under the following basic assumptions.
$T_{\infty }$
. The (uniform) temperature of the sphere is supposed to be the same as that of the gas at infinity. We investigate the steady behaviour of the gas induced around the sphere, under the following basic assumptions.
(i) The behaviour of the gas is described by the ellipsoidal statistical model (Holway Reference Holway1966; Andries et al. Reference Andries, Tallec, Perlat and Perthame2000), which we call the ES model, of the Boltzmann equation.
(ii) The gas molecules are reflected on the sphere surface according to the Maxwell diffuse–specular boundary condition (Sone Reference Sone2007).
(iii) The angular velocity of the sphere is sufficiently small, i.e.
 $|\unicode[STIX]{x1D6FA}^{\ast }|L/(2RT_{\infty })^{1/2}\ll 1$
, and the equation and boundary condition can be linearised around the reference equilibrium state at rest. Here,
$|\unicode[STIX]{x1D6FA}^{\ast }|L/(2RT_{\infty })^{1/2}\ll 1$
, and the equation and boundary condition can be linearised around the reference equilibrium state at rest. Here,
 $R$
is the specific gas constant (i.e. the Boltzmann constant divided by the mass of a molecule).
$R$
is the specific gas constant (i.e. the Boltzmann constant divided by the mass of a molecule).
We further assume that the state of the sphere surface is homogeneous and therefore the accommodation coefficient of the surface, denoted by
![]() $\unicode[STIX]{x1D6FC}$
, is a constant independent of the position on the surface. In the present study, we assume that the temperature of the sphere is uniform and is the same as that of the gas at infinity. A justification of this assumption is given in appendix A.
$\unicode[STIX]{x1D6FC}$
, is a constant independent of the position on the surface. In the present study, we assume that the temperature of the sphere is uniform and is the same as that of the gas at infinity. A justification of this assumption is given in appendix A.
2.2 Basic equations
Let us introduce the molecular velocity
![]() $(2RT_{\infty })^{1/2}\unicode[STIX]{x1D701}_{i}$
(or
$(2RT_{\infty })^{1/2}\unicode[STIX]{x1D701}_{i}$
(or
![]() $(2RT_{\infty })^{1/2}\unicode[STIX]{x1D73B}$
) and the VDF of the gas molecules
$(2RT_{\infty })^{1/2}\unicode[STIX]{x1D73B}$
) and the VDF of the gas molecules
![]() $\unicode[STIX]{x1D70C}_{\infty }(2RT_{\infty })^{-3/2}(1+\unicode[STIX]{x1D719}(\boldsymbol{x},\unicode[STIX]{x1D73B}))E$
, where
$\unicode[STIX]{x1D70C}_{\infty }(2RT_{\infty })^{-3/2}(1+\unicode[STIX]{x1D719}(\boldsymbol{x},\unicode[STIX]{x1D73B}))E$
, where
![]() $E=E(\unicode[STIX]{x1D701}_{i})=\unicode[STIX]{x03C0}^{-3/2}\exp (-\unicode[STIX]{x1D701}_{j}^{2})$
. We also denote by
$E=E(\unicode[STIX]{x1D701}_{i})=\unicode[STIX]{x03C0}^{-3/2}\exp (-\unicode[STIX]{x1D701}_{j}^{2})$
. We also denote by
![]() $\unicode[STIX]{x1D70C}_{\infty }(1+\unicode[STIX]{x1D714}(\boldsymbol{x}))$
the density, by
$\unicode[STIX]{x1D70C}_{\infty }(1+\unicode[STIX]{x1D714}(\boldsymbol{x}))$
the density, by
![]() $(2RT_{\infty })^{1/2}u_{i}(\boldsymbol{x})$
the flow velocity, by
$(2RT_{\infty })^{1/2}u_{i}(\boldsymbol{x})$
the flow velocity, by
![]() $T_{\infty }(1+\unicode[STIX]{x1D70F}(\boldsymbol{x}))$
the temperature, by
$T_{\infty }(1+\unicode[STIX]{x1D70F}(\boldsymbol{x}))$
the temperature, by
![]() $p_{\infty }(1+P(\boldsymbol{x}))$
the pressures, by
$p_{\infty }(1+P(\boldsymbol{x}))$
the pressures, by
![]() $p_{\infty }(\unicode[STIX]{x1D6FF}_{ij}+P_{ij}(\boldsymbol{x}))$
the stress tensor and by
$p_{\infty }(\unicode[STIX]{x1D6FF}_{ij}+P_{ij}(\boldsymbol{x}))$
the stress tensor and by
![]() $p_{\infty }(2RT_{\infty })^{1/2}Q_{i}(\boldsymbol{x})$
the heat-flow vector of the gas. Here,
$p_{\infty }(2RT_{\infty })^{1/2}Q_{i}(\boldsymbol{x})$
the heat-flow vector of the gas. Here,
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta and
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta and
![]() $p_{\infty }=R\unicode[STIX]{x1D70C}_{\infty }T_{\infty }$
. In the following, we also use the spherical coordinate system
$p_{\infty }=R\unicode[STIX]{x1D70C}_{\infty }T_{\infty }$
. In the following, we also use the spherical coordinate system
![]() $(Lr,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
with its polar direction directed to the
$(Lr,\unicode[STIX]{x1D703},\unicode[STIX]{x1D711})$
with its polar direction directed to the
![]() $x_{1}$
axis. The corresponding components of the molecular velocity are denoted by
$x_{1}$
axis. The corresponding components of the molecular velocity are denoted by
![]() $(2RT_{\infty })^{1/2}(\unicode[STIX]{x1D701}_{r},\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}})$
. A similar convention will be used throughout the paper for vectors and tensors (e.g.
$(2RT_{\infty })^{1/2}(\unicode[STIX]{x1D701}_{r},\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D703}},\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}})$
. A similar convention will be used throughout the paper for vectors and tensors (e.g.
![]() $(u_{r},u_{\unicode[STIX]{x1D703}},u_{\unicode[STIX]{x1D711}})$
etc.).
$(u_{r},u_{\unicode[STIX]{x1D703}},u_{\unicode[STIX]{x1D711}})$
etc.).
The linearised ES equation for the present steady problem reads
where
![]() ${\mathcal{L}}^{ES}$
is the linearised collision operator for the ES model with the so-called relaxation parameter
${\mathcal{L}}^{ES}$
is the linearised collision operator for the ES model with the so-called relaxation parameter
![]() $\unicode[STIX]{x1D708}\in [-1/2,1)$
,
$\unicode[STIX]{x1D708}\in [-1/2,1)$
,
and
![]() $k$
is defined by
$k$
is defined by
Here,
![]() $Kn$
is the Knudsen number with
$Kn$
is the Knudsen number with
![]() $\ell _{\infty }$
being the mean free path of the gas molecules in the equilibrium state at rest with temperature
$\ell _{\infty }$
being the mean free path of the gas molecules in the equilibrium state at rest with temperature
![]() $T_{\infty }$
and density
$T_{\infty }$
and density
![]() $\unicode[STIX]{x1D70C}_{\infty }$
, and
$\unicode[STIX]{x1D70C}_{\infty }$
, and
![]() $A_{c}$
is a constant such that
$A_{c}$
is a constant such that
![]() $A_{c}\unicode[STIX]{x1D70C}_{\infty }$
is the collision frequency at the reference state. In (2.4),
$A_{c}\unicode[STIX]{x1D70C}_{\infty }$
is the collision frequency at the reference state. In (2.4),
![]() $\text{d}\unicode[STIX]{x1D73B}=\text{d}\unicode[STIX]{x1D701}_{1}\,\text{d}\unicode[STIX]{x1D701}_{2}\,\text{d}\unicode[STIX]{x1D701}_{3}$
and the domain of integration is the whole space of
$\text{d}\unicode[STIX]{x1D73B}=\text{d}\unicode[STIX]{x1D701}_{1}\,\text{d}\unicode[STIX]{x1D701}_{2}\,\text{d}\unicode[STIX]{x1D701}_{3}$
and the domain of integration is the whole space of
![]() $\unicode[STIX]{x1D73B}$
.
$\unicode[STIX]{x1D73B}$
.
The Maxwell diffuse–specular boundary condition (or the Maxwell condition for short) on the sphere is written as
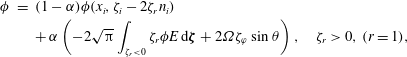 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719} & = & \displaystyle (1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D719}(x_{i},\unicode[STIX]{x1D701}_{i}-2\unicode[STIX]{x1D701}_{r}n_{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}\left(-2\sqrt{\unicode[STIX]{x03C0}}\int _{\unicode[STIX]{x1D701}_{r}<0}\unicode[STIX]{x1D701}_{r}\unicode[STIX]{x1D719}E\,\text{d}\unicode[STIX]{x1D73B}+2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}\right),\quad \unicode[STIX]{x1D701}_{r}>0,\,(r=1),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719} & = & \displaystyle (1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D719}(x_{i},\unicode[STIX]{x1D701}_{i}-2\unicode[STIX]{x1D701}_{r}n_{i})\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FC}\left(-2\sqrt{\unicode[STIX]{x03C0}}\int _{\unicode[STIX]{x1D701}_{r}<0}\unicode[STIX]{x1D701}_{r}\unicode[STIX]{x1D719}E\,\text{d}\unicode[STIX]{x1D73B}+2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}\right),\quad \unicode[STIX]{x1D701}_{r}>0,\,(r=1),\end{eqnarray}$$
where
![]() $n_{i}$
is the unit normal vector on the surface of the sphere pointed to the gas,
$n_{i}$
is the unit normal vector on the surface of the sphere pointed to the gas,
![]() $\unicode[STIX]{x1D701}_{r}=\unicode[STIX]{x1D701}_{i}n_{i}$
,
$\unicode[STIX]{x1D701}_{r}=\unicode[STIX]{x1D701}_{i}n_{i}$
,
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}^{\ast }L/(2RT_{\infty })^{1/2}$
and
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}^{\ast }L/(2RT_{\infty })^{1/2}$
and
![]() $\unicode[STIX]{x1D6FC}\in [0,1]$
is the accommodation coefficient. When
$\unicode[STIX]{x1D6FC}\in [0,1]$
is the accommodation coefficient. When
![]() $\unicode[STIX]{x1D6FC}=1$
, the specular reflection part of the condition (2.6) is absent and the condition is known as the diffuse reflection condition. The Maxwell boundary condition is a model, originally introduced by Maxwell, in which the molecules arriving at the boundary are reflected diffusely with probability
$\unicode[STIX]{x1D6FC}=1$
, the specular reflection part of the condition (2.6) is absent and the condition is known as the diffuse reflection condition. The Maxwell boundary condition is a model, originally introduced by Maxwell, in which the molecules arriving at the boundary are reflected diffusely with probability
![]() $\unicode[STIX]{x1D6FC}$
and specularly with probability
$\unicode[STIX]{x1D6FC}$
and specularly with probability
![]() $1-\unicode[STIX]{x1D6FC}$
. This model is the well-known gas–surface interaction model which can represent in a simplest way the non-perfect accommodation with the boundary of the reflected molecules. The simple combination of diffuse and specular reflections plays a key role in the subsequent discussions because it allows us to control the magnitude of the discontinuity in the VDF on the boundary by changing the parameter
$1-\unicode[STIX]{x1D6FC}$
. This model is the well-known gas–surface interaction model which can represent in a simplest way the non-perfect accommodation with the boundary of the reflected molecules. The simple combination of diffuse and specular reflections plays a key role in the subsequent discussions because it allows us to control the magnitude of the discontinuity in the VDF on the boundary by changing the parameter
![]() $\unicode[STIX]{x1D6FC}$
(the specular part produces no discontinuity on the boundary). Other models such as the Cercignani–Lampis model (Cercignani Reference Cercignani1988) do not represent the specular boundary and therefore are inadequate for the present purpose of quantifying the relation between the discontinuity and the diverging term in the macroscopic quantities. It is also expected that, though the Maxwell condition is unable to reproduce some physical details of actual molecular scatterings, a global property like the torque acting on the sphere is well represented by this model.
$\unicode[STIX]{x1D6FC}$
(the specular part produces no discontinuity on the boundary). Other models such as the Cercignani–Lampis model (Cercignani Reference Cercignani1988) do not represent the specular boundary and therefore are inadequate for the present purpose of quantifying the relation between the discontinuity and the diverging term in the macroscopic quantities. It is also expected that, though the Maxwell condition is unable to reproduce some physical details of actual molecular scatterings, a global property like the torque acting on the sphere is well represented by this model.
On the other hand, the state of the gas approaches the equilibrium state at rest with density
![]() $\unicode[STIX]{x1D70C}_{\infty }$
and temperature
$\unicode[STIX]{x1D70C}_{\infty }$
and temperature
![]() $T_{\infty }$
(and pressure
$T_{\infty }$
(and pressure
![]() $p_{\infty }$
) at infinity. Therefore, we have
$p_{\infty }$
) at infinity. Therefore, we have
The pressure and the heat-flow vector are defined by
If we set
![]() $\unicode[STIX]{x1D708}=0$
in the (linearised) ES collision operator (2.2), we obtain the well-known linearised BGK collision operator (Bhatnagar, Gross & Krook Reference Bhatnagar, Gross and Krook1954; Welander Reference Welander1954; Sone Reference Sone2007):
$\unicode[STIX]{x1D708}=0$
in the (linearised) ES collision operator (2.2), we obtain the well-known linearised BGK collision operator (Bhatnagar, Gross & Krook Reference Bhatnagar, Gross and Krook1954; Welander Reference Welander1954; Sone Reference Sone2007):
where
![]() $\unicode[STIX]{x1D714}$
,
$\unicode[STIX]{x1D714}$
,
![]() $u_{i}$
and
$u_{i}$
and
![]() $\unicode[STIX]{x1D70F}$
are still defined in (2.3).
$\unicode[STIX]{x1D70F}$
are still defined in (2.3).
When the state of the gas is close to the local equilibrium, the ES model yields the following viscosity
![]() $\unicode[STIX]{x1D707}_{\infty }$
and thermal conductivity
$\unicode[STIX]{x1D707}_{\infty }$
and thermal conductivity
![]() $\unicode[STIX]{x1D706}_{\infty }$
in the reference state:
$\unicode[STIX]{x1D706}_{\infty }$
in the reference state:
Consequently, the corresponding Prandtl number for the ES model, defined by the ratio of the kinematic viscosity to the thermal diffusivity, is given by
which is monotonically increasing in
![]() $\unicode[STIX]{x1D708}\in [-1/2,1)$
. The Prandtl number for a monatomic gas is close to
$\unicode[STIX]{x1D708}\in [-1/2,1)$
. The Prandtl number for a monatomic gas is close to
![]() $2/3$
both experimentally and theoretically (it is exactly
$2/3$
both experimentally and theoretically (it is exactly
![]() $2/3$
for pseudo-Maxwell molecules). As seen from (2.13), the ES model yields
$2/3$
for pseudo-Maxwell molecules). As seen from (2.13), the ES model yields
![]() $Pr=2/3$
by specifying the value
$Pr=2/3$
by specifying the value
![]() $\unicode[STIX]{x1D708}=-1/2$
. This means that the ES model has an ability to match both the viscosity and the thermal conductivity simultaneously to experimental data for monatomic gases, while tuning the mean free path. However, this favourable property is less important in the present linearised problem, because, as shown below (§ 2.3), the temperature of the gas is uniform and therefore the thermal conduction is irrelevant (note that the heat flux does not vanish in the gas though the temperature is uniform). Also, for the reason explained at the end of § 5,
$\unicode[STIX]{x1D708}=-1/2$
. This means that the ES model has an ability to match both the viscosity and the thermal conductivity simultaneously to experimental data for monatomic gases, while tuning the mean free path. However, this favourable property is less important in the present linearised problem, because, as shown below (§ 2.3), the temperature of the gas is uniform and therefore the thermal conduction is irrelevant (note that the heat flux does not vanish in the gas though the temperature is uniform). Also, for the reason explained at the end of § 5,
![]() $\unicode[STIX]{x1D708}$
(or
$\unicode[STIX]{x1D708}$
(or
![]() $Pr$
) is considered as a free parameter and will not be specialised to
$Pr$
) is considered as a free parameter and will not be specialised to
![]() $\unicode[STIX]{x1D708}=-1/2$
(or
$\unicode[STIX]{x1D708}=-1/2$
(or
![]() $Pr=2/3$
) in this study.
$Pr=2/3$
) in this study.
In the original (nonlinear) ES model, the Boltzmann collision term is replaced by a relaxation operator, which is computationally more tractable. It can be viewed as an extension of the BGK model (for which
![]() $\unicode[STIX]{x1D708}=0$
), and has an advantage over other similar models in that the Boltzmann H theorem has been proved for
$\unicode[STIX]{x1D708}=0$
), and has an advantage over other similar models in that the Boltzmann H theorem has been proved for
![]() $-1/2\leqslant \unicode[STIX]{x1D708}<1$
(Andries et al.
Reference Andries, Tallec, Perlat and Perthame2000). The modification of the original Boltzmann collision operator may lose some details of the two-body collision mechanics involved in the original collision kernel but retains the important basic properties. Moreover, it has been shown in various flow problems that the adjustment of the mean free path in terms of viscosity or thermal conductivity in accordance with the problem and the quantity under consideration is required to have quantitatively a good agreement between the BGK model and the Boltzmann equation. Various extensions of the ES model have also been proposed in the context of gas mixtures (Brull Reference Brull2015) and polyatomic gases (Andries et al.
Reference Andries, Tallec, Perlat and Perthame2000).
$-1/2\leqslant \unicode[STIX]{x1D708}<1$
(Andries et al.
Reference Andries, Tallec, Perlat and Perthame2000). The modification of the original Boltzmann collision operator may lose some details of the two-body collision mechanics involved in the original collision kernel but retains the important basic properties. Moreover, it has been shown in various flow problems that the adjustment of the mean free path in terms of viscosity or thermal conductivity in accordance with the problem and the quantity under consideration is required to have quantitatively a good agreement between the BGK model and the Boltzmann equation. Various extensions of the ES model have also been proposed in the context of gas mixtures (Brull Reference Brull2015) and polyatomic gases (Andries et al.
Reference Andries, Tallec, Perlat and Perthame2000).
2.3 Similarity solution
The following similarity solution is compatible for the present problem:
where
![]() $\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{i}^{2})^{1/2}=(\unicode[STIX]{x1D701}_{r}^{2}+\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D703}}^{2}+\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}^{2})^{1/2}$
. With this similarity solution, the problem is reduced to the following spatially one-dimensional problem for
$\unicode[STIX]{x1D701}=(\unicode[STIX]{x1D701}_{i}^{2})^{1/2}=(\unicode[STIX]{x1D701}_{r}^{2}+\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D703}}^{2}+\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}^{2})^{1/2}$
. With this similarity solution, the problem is reduced to the following spatially one-dimensional problem for
![]() $\unicode[STIX]{x1D719}_{S}$
:
$\unicode[STIX]{x1D719}_{S}$
:
where
Substituting (2.14) into (2.3) and (2.8), we find that the macroscopic quantities take the following forms:
Corresponding to (2.9), we have
Multiplying (2.1) by
![]() $\unicode[STIX]{x1D701}_{i}E$
and integrating the result with respect to
$\unicode[STIX]{x1D701}_{i}E$
and integrating the result with respect to
![]() $\unicode[STIX]{x1D73B}$
yield
$\unicode[STIX]{x1D73B}$
yield
![]() $\unicode[STIX]{x2202}P_{ij}/\unicode[STIX]{x2202}x_{j}=0$
, from which one can show that
$\unicode[STIX]{x2202}P_{ij}/\unicode[STIX]{x2202}x_{j}=0$
, from which one can show that
![]() $\text{d}(r^{3}\widetilde{P}_{r\unicode[STIX]{x1D711}})/\text{d}r=0$
, or equivalently
$\text{d}(r^{3}\widetilde{P}_{r\unicode[STIX]{x1D711}})/\text{d}r=0$
, or equivalently
Therefore,
![]() $r^{3}\widetilde{P}_{r\unicode[STIX]{x1D711}}$
is a conserved quantity of the problem. In § 3, this property plays a crucial role in finding a conversion relation between the ES and BGK models (see also, e.g. Cercignani Reference Cercignani1988; Takata, Hattori & Hasebe Reference Takata, Hattori and Hasebe2016a
, and references therein).
$r^{3}\widetilde{P}_{r\unicode[STIX]{x1D711}}$
is a conserved quantity of the problem. In § 3, this property plays a crucial role in finding a conversion relation between the ES and BGK models (see also, e.g. Cercignani Reference Cercignani1988; Takata, Hattori & Hasebe Reference Takata, Hattori and Hasebe2016a
, and references therein).
If we denote by
![]() $p_{\infty }L^{3}(M,0,0)$
the moment of force (torque) acting on the sphere,
$p_{\infty }L^{3}(M,0,0)$
the moment of force (torque) acting on the sphere,
![]() $M$
is given by
$M$
is given by
where
![]() $\unicode[STIX]{x1D716}_{ijk}$
is the Eddington epsilon and
$\unicode[STIX]{x1D716}_{ijk}$
is the Eddington epsilon and
![]() $\text{d}S$
is the surface element on the sphere. By the use of (2.20b
), it is further simplified to
$\text{d}S$
is the surface element on the sphere. By the use of (2.20b
), it is further simplified to
Thus, if we express
![]() $M$
as
$M$
as
![]() $h_{M}=h_{M}(k,Pr,\unicode[STIX]{x1D6FC})$
is given by
$h_{M}=h_{M}(k,Pr,\unicode[STIX]{x1D6FC})$
is given by
where (2.24) has been used for the second equality. Note that dimensionless torque
![]() $h_{M}$
depends not only on
$h_{M}$
depends not only on
![]() $k$
and
$k$
and
![]() $Pr$
(or
$Pr$
(or
![]() $\unicode[STIX]{x1D708}$
), but also on
$\unicode[STIX]{x1D708}$
), but also on
![]() $\unicode[STIX]{x1D6FC}$
through the boundary condition; hence, the functional dependency is
$\unicode[STIX]{x1D6FC}$
through the boundary condition; hence, the functional dependency is
![]() $h_{M}=h_{M}(k,Pr,\unicode[STIX]{x1D6FC})$
. One of our interests is to construct
$h_{M}=h_{M}(k,Pr,\unicode[STIX]{x1D6FC})$
. One of our interests is to construct
![]() $h_{M}(k,Pr,\unicode[STIX]{x1D6FC})$
for the ES model for a wide range of the parameter space.
$h_{M}(k,Pr,\unicode[STIX]{x1D6FC})$
for the ES model for a wide range of the parameter space.
No net force acts on the sphere in the present problem.
In our formulation, the problem has been linearised about the reference equilibrium state at rest under the condition of slow rotation, i.e.
![]() $|\unicode[STIX]{x1D6FA}|=|\unicode[STIX]{x1D6FA}^{\ast }|L/(2RT_{\infty })^{1/2}\ll 1$
. Since the domain is unbounded, it is important to determine the range of
$|\unicode[STIX]{x1D6FA}|=|\unicode[STIX]{x1D6FA}^{\ast }|L/(2RT_{\infty })^{1/2}\ll 1$
. Since the domain is unbounded, it is important to determine the range of
![]() $r$
in which the linearisation is valid. In this problem, the perturbed VDF
$r$
in which the linearisation is valid. In this problem, the perturbed VDF
![]() $\unicode[STIX]{x1D719}$
decays like
$\unicode[STIX]{x1D719}$
decays like
![]() $r^{-2}$
as
$r^{-2}$
as
![]() $r\rightarrow \infty$
when
$r\rightarrow \infty$
when
![]() $k<\infty$
. Consequently, the nonlinear term remains smaller than the transport term (i.e. the left-hand side of (2.1)) as
$k<\infty$
. Consequently, the nonlinear term remains smaller than the transport term (i.e. the left-hand side of (2.1)) as
![]() $r$
is increased, implying that the linearisation is valid uniformly in the whole gas region. The situation is therefore different from that of a slow uniform flow past a sphere, for which a matched expansion approach is required to treat the nonlinear effect in the region far from the sphere (Taguchi Reference Taguchi2015; Taguchi & Suzuki Reference Taguchi and Suzuki2017).
$r$
is increased, implying that the linearisation is valid uniformly in the whole gas region. The situation is therefore different from that of a slow uniform flow past a sphere, for which a matched expansion approach is required to treat the nonlinear effect in the region far from the sphere (Taguchi Reference Taguchi2015; Taguchi & Suzuki Reference Taguchi and Suzuki2017).
3 Relation between the solutions for the ES model and the BGK model
The problem contains three parameters:
![]() $k$
,
$k$
,
![]() $Pr$
(or
$Pr$
(or
![]() $\unicode[STIX]{x1D708}$
) and
$\unicode[STIX]{x1D708}$
) and
![]() $\unicode[STIX]{x1D6FC}$
. Hence, the necessary amount of computations is quite large. Fortunately, in the case of the ES model, one can express the solution for arbitrary
$\unicode[STIX]{x1D6FC}$
. Hence, the necessary amount of computations is quite large. Fortunately, in the case of the ES model, one can express the solution for arbitrary
![]() $\unicode[STIX]{x1D708}$
in terms of the solution for
$\unicode[STIX]{x1D708}$
in terms of the solution for
![]() $\unicode[STIX]{x1D708}=0$
(the BGK model), thereby reducing the amount of computations. In this section, for the sake of discrimination, we denote the solution of the boundary-value problem (2.15)–(2.17) based on the ES model and that based on the BGK model by
$\unicode[STIX]{x1D708}=0$
(the BGK model), thereby reducing the amount of computations. In this section, for the sake of discrimination, we denote the solution of the boundary-value problem (2.15)–(2.17) based on the ES model and that based on the BGK model by
![]() $\unicode[STIX]{x1D719}_{S}^{ES}$
and
$\unicode[STIX]{x1D719}_{S}^{ES}$
and
![]() $\unicode[STIX]{x1D719}_{S}^{BGK}$
, respectively (i.e.
$\unicode[STIX]{x1D719}_{S}^{BGK}$
, respectively (i.e.
![]() $\unicode[STIX]{x1D719}_{S}^{BGK}=\unicode[STIX]{x1D719}_{S}^{ES}|_{\unicode[STIX]{x1D708}=0}$
). Likewise, the corresponding macroscopic quantities are distinguished using the superscript ‘ES’ or ‘BGK’.
$\unicode[STIX]{x1D719}_{S}^{BGK}=\unicode[STIX]{x1D719}_{S}^{ES}|_{\unicode[STIX]{x1D708}=0}$
). Likewise, the corresponding macroscopic quantities are distinguished using the superscript ‘ES’ or ‘BGK’.
Supposing that
![]() $\unicode[STIX]{x1D719}_{S}^{BGK}$
is known, we seek
$\unicode[STIX]{x1D719}_{S}^{BGK}$
is known, we seek
![]() $\unicode[STIX]{x1D719}_{S}^{ES}$
in the form
$\unicode[STIX]{x1D719}_{S}^{ES}$
in the form
where
![]() $a$
is a function of
$a$
is a function of
![]() $r$
and
$r$
and
![]() $b$
is independent of
$b$
is independent of
![]() $(r,\unicode[STIX]{x1D701}_{r},\unicode[STIX]{x1D701})$
. Because of the linearity of
$(r,\unicode[STIX]{x1D701}_{r},\unicode[STIX]{x1D701})$
. Because of the linearity of
![]() ${\mathcal{L}}_{1}^{ES}$
and
${\mathcal{L}}_{1}^{ES}$
and
![]() ${\mathcal{L}}_{1}^{ES}[1]=0$
, we deduce
${\mathcal{L}}_{1}^{ES}[1]=0$
, we deduce
Thus, the subtraction of (2.15) for
![]() $\unicode[STIX]{x1D708}=0$
with
$\unicode[STIX]{x1D708}=0$
with
![]() $\unicode[STIX]{x1D719}_{S}=b\unicode[STIX]{x1D719}_{S}^{BGK}$
from (2.15) with
$\unicode[STIX]{x1D719}_{S}=b\unicode[STIX]{x1D719}_{S}^{BGK}$
from (2.15) with
![]() $\unicode[STIX]{x1D719}_{S}=\unicode[STIX]{x1D719}_{S}^{ES}$
leads to
$\unicode[STIX]{x1D719}_{S}=\unicode[STIX]{x1D719}_{S}^{ES}$
leads to
or equivalently,
On the other hand, equation (2.24) allows one to write
Substituting this into (3.4) and integrating the result with respect to
![]() $r$
yield
$r$
yield
where
![]() $\unicode[STIX]{x1D6FD}$
is an integration constant.
$\unicode[STIX]{x1D6FD}$
is an integration constant.
The constants
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $b$
are determined as follows. First, condition (2.17) at infinity requires
$b$
are determined as follows. First, condition (2.17) at infinity requires
![]() $a\rightarrow 0$
as
$a\rightarrow 0$
as
![]() $r\rightarrow \infty$
, and hence
$r\rightarrow \infty$
, and hence
![]() $\unicode[STIX]{x1D6FD}=0$
. Next, after noting that both
$\unicode[STIX]{x1D6FD}=0$
. Next, after noting that both
![]() $\unicode[STIX]{x1D719}_{S}^{ES}$
and
$\unicode[STIX]{x1D719}_{S}^{ES}$
and
![]() $\unicode[STIX]{x1D719}_{S}^{BGK}$
satisfy the boundary condition (2.16) at
$\unicode[STIX]{x1D719}_{S}^{BGK}$
satisfy the boundary condition (2.16) at
![]() $r=1$
independently (for the same
$r=1$
independently (for the same
![]() $\unicode[STIX]{x1D6FC}>0$
), we have
$\unicode[STIX]{x1D6FC}>0$
), we have
Applying this to (3.6) (with
![]() $\unicode[STIX]{x1D6FD}=0$
) determines
$\unicode[STIX]{x1D6FD}=0$
) determines
![]() $b$
, and hence
$b$
, and hence
![]() $a(r)$
, as follows:
$a(r)$
, as follows:
To summarise,
![]() $\unicode[STIX]{x1D719}_{S}^{ES}$
is expressed in terms of
$\unicode[STIX]{x1D719}_{S}^{ES}$
is expressed in terms of
![]() $\unicode[STIX]{x1D719}_{S}^{BGK}$
as
$\unicode[STIX]{x1D719}_{S}^{BGK}$
as
where we have replaced
![]() $\widetilde{P}_{r\unicode[STIX]{x1D711}}^{BGK}|_{r=1}$
and
$\widetilde{P}_{r\unicode[STIX]{x1D711}}^{BGK}|_{r=1}$
and
![]() $\unicode[STIX]{x1D708}$
by
$\unicode[STIX]{x1D708}$
by
![]() $h_{M}^{BGK}$
$h_{M}^{BGK}$
![]() $(\equiv h_{M}(k,1,\unicode[STIX]{x1D6FC}))$
and
$(\equiv h_{M}(k,1,\unicode[STIX]{x1D6FC}))$
and
![]() $Pr$
, respectively, by the use of the relation
$Pr$
, respectively, by the use of the relation
![]() $h_{M}^{BGK}=-(8/3)\unicode[STIX]{x03C0}\widetilde{P}_{r\unicode[STIX]{x1D711}}^{BGK}|_{r=1}$
and (2.13). The corresponding formulas for the macroscopic variables (i.e. the moments of
$h_{M}^{BGK}=-(8/3)\unicode[STIX]{x03C0}\widetilde{P}_{r\unicode[STIX]{x1D711}}^{BGK}|_{r=1}$
and (2.13). The corresponding formulas for the macroscopic variables (i.e. the moments of
![]() $\unicode[STIX]{x1D719}_{S}$
) are summarised as
$\unicode[STIX]{x1D719}_{S}$
) are summarised as
With the aid of these relations, one can readily obtain the solution for the ES model from that for the BGK model (
![]() $Pr=1$
or
$Pr=1$
or
![]() $\unicode[STIX]{x1D708}=0$
) for the common
$\unicode[STIX]{x1D708}=0$
) for the common
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FC}$
. Moreover, the relation can be used to check the accuracy of numerical computation, if one has solutions for
$\unicode[STIX]{x1D6FC}$
. Moreover, the relation can be used to check the accuracy of numerical computation, if one has solutions for
![]() $Pr=1$
and
$Pr=1$
and
![]() $Pr\neq 1$
for the same
$Pr\neq 1$
for the same
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
4 Results for large and small
 $k$
$k$
Before proceeding to the actual numerical analysis, we summarise here some analytical results available for large and small
![]() $k$
. The formulas given in this section are not restricted to the ES model.
$k$
. The formulas given in this section are not restricted to the ES model.
The solution in the case of a collisionless gas, i.e.
![]() $k=\infty$
, is easily obtained for the present problem and is given by
$k=\infty$
, is easily obtained for the present problem and is given by
Here,
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}$
(
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}$
(
![]() $0\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}$
) is the polar angle of the molecular velocity
$0\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}$
) is the polar angle of the molecular velocity
![]() $\unicode[STIX]{x1D701}_{i}$
measured from the radial direction, i.e.
$\unicode[STIX]{x1D701}_{i}$
measured from the radial direction, i.e.
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\text{Arccos}(\unicode[STIX]{x1D701}_{r}/\unicode[STIX]{x1D701})$
. Thus, the solution is simply proportional to
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\text{Arccos}(\unicode[STIX]{x1D701}_{r}/\unicode[STIX]{x1D701})$
. Thus, the solution is simply proportional to
![]() $\unicode[STIX]{x1D6FC}$
in the case of the collisionless gas. The macroscopic quantities and the torque acting on the sphere are easily obtained and are summarised as follows:
$\unicode[STIX]{x1D6FC}$
in the case of the collisionless gas. The macroscopic quantities and the torque acting on the sphere are easily obtained and are summarised as follows:
Thus, the heat flow vanishes in the collisionless limit. From the above expression, it is easily seen that
![]() $\text{d}\widetilde{u}_{\unicode[STIX]{x1D711}}/\text{d}r$
diverges with the rate
$\text{d}\widetilde{u}_{\unicode[STIX]{x1D711}}/\text{d}r$
diverges with the rate
![]() $(r-1)^{-1/2}$
as
$(r-1)^{-1/2}$
as
![]() $r\downarrow 1$
.
$r\downarrow 1$
.
The asymptotic expressions of the flow field for
![]() $k\ll 1$
are obtained with the aid of the asymptotic theory (the generalised slip flow theory) (Sone Reference Sone2002, Reference Sone2007). We summarise the results in the case of
$k\ll 1$
are obtained with the aid of the asymptotic theory (the generalised slip flow theory) (Sone Reference Sone2002, Reference Sone2007). We summarise the results in the case of
![]() $\unicode[STIX]{x1D6FC}=1$
:
$\unicode[STIX]{x1D6FC}=1$
:
where
and
![]() $\unicode[STIX]{x1D702}=(r-1)/k$
. We note that
$\unicode[STIX]{x1D702}=(r-1)/k$
. We note that
![]() $\unicode[STIX]{x1D6FE}_{1}k$
is the dimensionless viscosity (
$\unicode[STIX]{x1D6FE}_{1}k$
is the dimensionless viscosity (
![]() $(\sqrt{\unicode[STIX]{x03C0}}/2)\unicode[STIX]{x1D6FE}_{1}p_{\infty }(2RT_{\infty })^{-1/2}\ell _{\infty }$
is the viscosity, where
$(\sqrt{\unicode[STIX]{x03C0}}/2)\unicode[STIX]{x1D6FE}_{1}p_{\infty }(2RT_{\infty })^{-1/2}\ell _{\infty }$
is the viscosity, where
![]() $\unicode[STIX]{x1D6FE}_{1}=1/(1-\unicode[STIX]{x1D708})=Pr$
for the ES model,
$\unicode[STIX]{x1D6FE}_{1}=1/(1-\unicode[STIX]{x1D708})=Pr$
for the ES model,
![]() $\unicode[STIX]{x1D6FE}_{1}=1$
for the BGK model and
$\unicode[STIX]{x1D6FE}_{1}=1$
for the BGK model and
![]() $\unicode[STIX]{x1D6FE}_{1}=1.270042427$
for the hard-sphere model),
$\unicode[STIX]{x1D6FE}_{1}=1.270042427$
for the hard-sphere model),
![]() $k_{0}$
,
$k_{0}$
,
![]() $a_{1}$
,
$a_{1}$
,
![]() $a_{2}$
and
$a_{2}$
and
![]() $a_{3}$
are the slip coefficients and
$a_{3}$
are the slip coefficients and
![]() $Y_{0}(\unicode[STIX]{x1D702})$
,
$Y_{0}(\unicode[STIX]{x1D702})$
,
![]() $Y_{a1}(\unicode[STIX]{x1D702})$
,
$Y_{a1}(\unicode[STIX]{x1D702})$
,
![]() $Y_{a2}(\unicode[STIX]{x1D702})$
,
$Y_{a2}(\unicode[STIX]{x1D702})$
,
![]() $Y_{a3}(\unicode[STIX]{x1D702})$
and
$Y_{a3}(\unicode[STIX]{x1D702})$
and
![]() $H_{A}(\unicode[STIX]{x1D702})$
are the Knudsen-layer functions (Sone Reference Sone2007). The slip coefficients and the Knudsen-layer functions depend on the molecular model as well as on the model of the molecular scattering law on the surface. The values for the ES model under the diffuse reflection boundary condition, i.e.
$H_{A}(\unicode[STIX]{x1D702})$
are the Knudsen-layer functions (Sone Reference Sone2007). The slip coefficients and the Knudsen-layer functions depend on the molecular model as well as on the model of the molecular scattering law on the surface. The values for the ES model under the diffuse reflection boundary condition, i.e.
![]() $\unicode[STIX]{x1D6FC}=1$
, have recently been obtained in Takata et al. (Reference Takata, Hattori and Hasebe2016a
). In that study, it was shown that the above slip coefficients and the Knudsen-layer functions for the ES model are related to those for the BGK model (i.e.
$\unicode[STIX]{x1D6FC}=1$
, have recently been obtained in Takata et al. (Reference Takata, Hattori and Hasebe2016a
). In that study, it was shown that the above slip coefficients and the Knudsen-layer functions for the ES model are related to those for the BGK model (i.e.
![]() $Pr=1$
) by the following simple relations:
$Pr=1$
) by the following simple relations:
where the subscripts ‘ES’ and ‘BGK’ stand for the slip coefficients and Knudsen-layer functions for the ES model and for the BGK model, respectively. We list the values of the slip coefficients for the BGK model and those for the ES model with
![]() $Pr=2/3$
under the diffuse reflection boundary condition in table 1. For the ES model with
$Pr=2/3$
under the diffuse reflection boundary condition in table 1. For the ES model with
![]() $Pr=2/3$
, the combination
$Pr=2/3$
, the combination
![]() $3k_{0}^{2}-3a_{1}+a_{2}+a_{3}$
, occurring at the third term in
$3k_{0}^{2}-3a_{1}+a_{2}+a_{3}$
, occurring at the third term in
![]() $\widetilde{u}_{\unicode[STIX]{x1D711}}$
,
$\widetilde{u}_{\unicode[STIX]{x1D711}}$
,
![]() $\widetilde{P}_{r\unicode[STIX]{x1D711}}$
and
$\widetilde{P}_{r\unicode[STIX]{x1D711}}$
and
![]() $h_{M}$
, turns out to be practically zero.
$h_{M}$
, turns out to be practically zero.
Table 1. The slip coefficients occurring in (4.4a
)–(4.4c
) for the BGK model, for the ES model with
![]() $Pr=2/3$
and for the hard-sphere gas (HS) under the diffuse reflection boundary condition (or the Maxwell boundary condition with
$Pr=2/3$
and for the hard-sphere gas (HS) under the diffuse reflection boundary condition (or the Maxwell boundary condition with
![]() $\unicode[STIX]{x1D6FC}=1$
). Data taken from Sone (Reference Sone2007) and Takata et al. (Reference Takata, Hattori and Hasebe2016a
).
$\unicode[STIX]{x1D6FC}=1$
). Data taken from Sone (Reference Sone2007) and Takata et al. (Reference Takata, Hattori and Hasebe2016a
).

We note that the S-layer corrections, which are required at the bottom of the Knudsen layer (Sone & Takata Reference Sone and Takata1992), have not been included in the above formulas for
![]() $\widetilde{u}_{\unicode[STIX]{x1D711}}$
and
$\widetilde{u}_{\unicode[STIX]{x1D711}}$
and
![]() $\widetilde{Q}_{\unicode[STIX]{x1D711}}$
for
$\widetilde{Q}_{\unicode[STIX]{x1D711}}$
for
![]() $k\ll 1$
.
$k\ll 1$
.
5 Numerical results
We solved the boundary-value problem (2.15)–(2.17) numerically by a finite difference method. The main feature of the present problem is the propagation of the discontinuity of the VDF in the phase space along the characteristics
![]() $r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=1$
(
$r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=1$
(
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\text{Arccos}(\unicode[STIX]{x1D701}_{r}/\unicode[STIX]{x1D701})$
). In order to capture this feature accurately, our method is based on a hybrid scheme consisting of a finite difference method and a method of characteristics. Its original form, among its variants, was developed for an evaporating flow from a cylindrical condensed phase (Sugimoto & Sone Reference Sugimoto and Sone1992) and then applied to the problem of a slow uniform flow past a sphere (Takata, Sone & Aoki Reference Takata, Sone and Aoki1993). Recently, the process of calculating the discontinuity was refined in Taguchi & Suzuki (Reference Taguchi and Suzuki2017). The numerical computations were carried out for
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\text{Arccos}(\unicode[STIX]{x1D701}_{r}/\unicode[STIX]{x1D701})$
). In order to capture this feature accurately, our method is based on a hybrid scheme consisting of a finite difference method and a method of characteristics. Its original form, among its variants, was developed for an evaporating flow from a cylindrical condensed phase (Sugimoto & Sone Reference Sugimoto and Sone1992) and then applied to the problem of a slow uniform flow past a sphere (Takata, Sone & Aoki Reference Takata, Sone and Aoki1993). Recently, the process of calculating the discontinuity was refined in Taguchi & Suzuki (Reference Taguchi and Suzuki2017). The numerical computations were carried out for
![]() $Pr=1$
(or
$Pr=1$
(or
![]() $\unicode[STIX]{x1D708}=0$
) and
$\unicode[STIX]{x1D708}=0$
) and
![]() $Pr=2/3$
(or
$Pr=2/3$
(or
![]() $\unicode[STIX]{x1D708}=-0.5$
), and for various values of the accommodation coefficient
$\unicode[STIX]{x1D708}=-0.5$
), and for various values of the accommodation coefficient
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
It should be emphasised that a proper account of the discontinuity in the VDF is crucial for the purpose of the present study. Loyalka (Reference Loyalka1992) solved the same problem numerically by using the Legendre polynomial expansion (truncated at the fourth term) of the linearised collision kernel for a hard-sphere gas. However, probably due to his main interest in the global quantities (e.g. the torque), the discontinuity of the velocity distribution was not taken into account there. In the present study, numerical computations were carried out carefully and faithfully at the level of the VDF in order to achieve the high accuracy required to reveal precise structures of the flow field. This is computationally quite challenging even with the ES or BGK model.
5.1 Behaviour of the macroscopic quantities
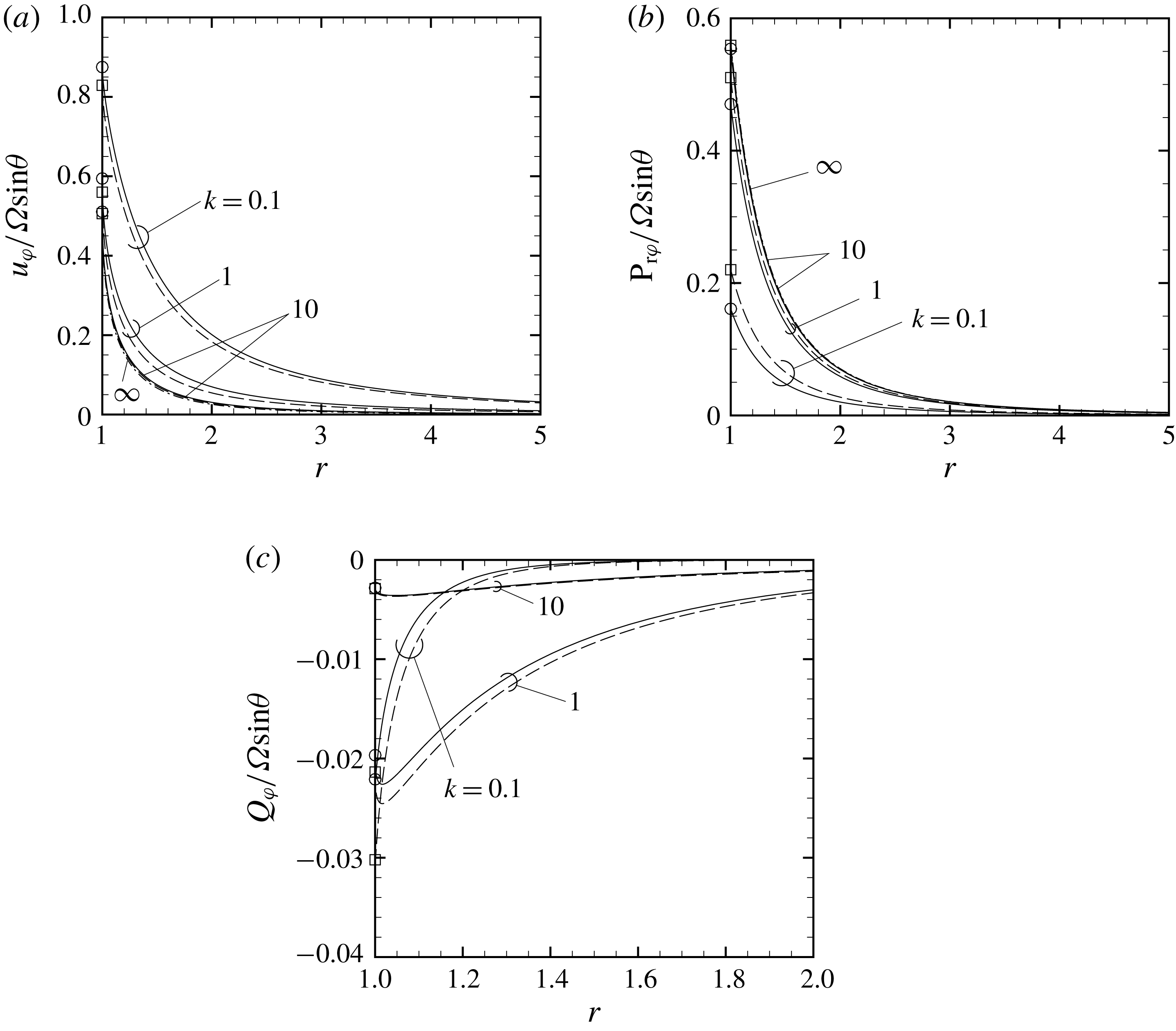
Figure 1. Profiles of the macroscopic quantities in the case of
![]() $\unicode[STIX]{x1D6FC}=1$
(the diffuse reflection boundary condition): (a)
$\unicode[STIX]{x1D6FC}=1$
(the diffuse reflection boundary condition): (a)
![]() $u_{\unicode[STIX]{x1D711}}$
, (b)
$u_{\unicode[STIX]{x1D711}}$
, (b)
![]() $P_{r\unicode[STIX]{x1D711}}$
, (c)
$P_{r\unicode[STIX]{x1D711}}$
, (c)
![]() $Q_{\unicode[STIX]{x1D711}}$
. The solid line indicates the results for
$Q_{\unicode[STIX]{x1D711}}$
. The solid line indicates the results for
![]() $Pr=2/3$
and the dashed line those for
$Pr=2/3$
and the dashed line those for
![]() $Pr=1$
. The value at
$Pr=1$
. The value at
![]() $r=1$
is indicated by ○ for
$r=1$
is indicated by ○ for
![]() $Pr=2/3$
and by ▫ for
$Pr=2/3$
and by ▫ for
![]() $Pr=1$
.
$Pr=1$
.
We first show the behaviour of the macroscopic quantities. Figure 1 shows the profiles of
![]() $u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
,
$u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
,
![]() $P_{r\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
and
$P_{r\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
and
![]() $Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
in the case of diffuse reflection (
$Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
in the case of diffuse reflection (
![]() $\unicode[STIX]{x1D6FC}=1$
) for
$\unicode[STIX]{x1D6FC}=1$
) for
![]() $k=0.1$
, 1 and 10. The solid line indicates the results for
$k=0.1$
, 1 and 10. The solid line indicates the results for
![]() $Pr=2/3$
and the dashed line those for
$Pr=2/3$
and the dashed line those for
![]() $Pr=1$
(or the BGK model). A flow is induced around the sphere due to the sphere rotation. The flow speed is faster for
$Pr=1$
(or the BGK model). A flow is induced around the sphere due to the sphere rotation. The flow speed is faster for
![]() $Pr=2/3$
than for
$Pr=2/3$
than for
![]() $Pr=1$
for the same
$Pr=1$
for the same
![]() $k$
. On the other hand, the flow speed is larger for smaller
$k$
. On the other hand, the flow speed is larger for smaller
![]() $k$
and approaches the limit
$k$
and approaches the limit
![]() $u_{\unicode[STIX]{x1D711}}\rightarrow \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}/r^{2}$
as
$u_{\unicode[STIX]{x1D711}}\rightarrow \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}/r^{2}$
as
![]() $k\rightarrow 0$
. The tangential stress
$k\rightarrow 0$
. The tangential stress
![]() $P_{r\unicode[STIX]{x1D711}}$
is inversely proportional to
$P_{r\unicode[STIX]{x1D711}}$
is inversely proportional to
![]() $r^{3}$
as seen from (2.24). There occurs a heat flux flowing in the opposite direction to the mass flow when
$r^{3}$
as seen from (2.24). There occurs a heat flux flowing in the opposite direction to the mass flow when
![]() $0<k<\infty$
, in spite that the temperature is uniform. Note that this heat flow, however, vanishes in the collisionless limit (see (4.2c
)).
$0<k<\infty$
, in spite that the temperature is uniform. Note that this heat flow, however, vanishes in the collisionless limit (see (4.2c
)).
Figure 2. Profiles of
![]() $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
![]() $Q_{\unicode[STIX]{x1D711}}$
for various
$Q_{\unicode[STIX]{x1D711}}$
for various
![]() $\unicode[STIX]{x1D6FC}$
in the case of
$\unicode[STIX]{x1D6FC}$
in the case of
![]() $Pr=2/3$
: (a,b)
$Pr=2/3$
: (a,b)
![]() $k=0.1$
, (c,d)
$k=0.1$
, (c,d)
![]() $k=1$
, (e,f)
$k=1$
, (e,f)
![]() $k=10$
. The value at
$k=10$
. The value at
![]() $r=1$
is indicated by ○.
$r=1$
is indicated by ○.
Next, in order to see the effect of the accommodation coefficient
![]() $\unicode[STIX]{x1D6FC}$
, the profiles of
$\unicode[STIX]{x1D6FC}$
, the profiles of
![]() $u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
and
$u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
and
![]() $Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
for various
$Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703}$
for various
![]() $\unicode[STIX]{x1D6FC}$
(
$\unicode[STIX]{x1D6FC}$
(
![]() $\unicode[STIX]{x1D6FC}=1$
, 0.6 and 0.2) are presented in figure 2 in the case of
$\unicode[STIX]{x1D6FC}=1$
, 0.6 and 0.2) are presented in figure 2 in the case of
![]() $Pr=2/3$
(
$Pr=2/3$
(
![]() $k=0.1$
, 1 and 10). The magnitude of the flow velocity and that of the heat flux decrease with a decrease of
$k=0.1$
, 1 and 10). The magnitude of the flow velocity and that of the heat flux decrease with a decrease of
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
We have seen that the gradient of the tangential flow velocity
![]() $\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
diverges on the boundary
$\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
diverges on the boundary
![]() $r=1$
in the case of collisionless flow (
$r=1$
in the case of collisionless flow (
![]() $k=\infty$
). It is also seen from figures 1 and 2 that
$k=\infty$
). It is also seen from figures 1 and 2 that
![]() $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
![]() $Q_{\unicode[STIX]{x1D711}}$
vary sharply near the boundary
$Q_{\unicode[STIX]{x1D711}}$
vary sharply near the boundary
![]() $r=1$
. Though it is difficult to see from the figure, the heat flux
$r=1$
. Though it is difficult to see from the figure, the heat flux
![]() $Q_{\unicode[STIX]{x1D711}}$
for
$Q_{\unicode[STIX]{x1D711}}$
for
![]() $\unicode[STIX]{x1D6FC}=0.2$
is also seen to vary quite sharply near
$\unicode[STIX]{x1D6FC}=0.2$
is also seen to vary quite sharply near
![]() $r=1$
if the figure is enlarged. In order to see this behaviour more clearly, we show in figure 3 the variations of
$r=1$
if the figure is enlarged. In order to see this behaviour more clearly, we show in figure 3 the variations of
![]() $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
![]() $Q_{\unicode[STIX]{x1D711}}$
near the boundary as functions of
$Q_{\unicode[STIX]{x1D711}}$
near the boundary as functions of
![]() $s=r-1$
for
$s=r-1$
for
![]() $k=10$
, 1 and 0.1, in the case of the diffuse reflection boundary condition (
$k=10$
, 1 and 0.1, in the case of the diffuse reflection boundary condition (
![]() $\unicode[STIX]{x1D6FC}=1$
). Clearly, these quantities approach their boundary values in proportion to
$\unicode[STIX]{x1D6FC}=1$
). Clearly, these quantities approach their boundary values in proportion to
![]() $s^{1/2}$
for each Knudsen number, implying that the divergence of
$s^{1/2}$
for each Knudsen number, implying that the divergence of
![]() $\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
and
$\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
and
![]() $\unicode[STIX]{x2202}Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
occurs at
$\unicode[STIX]{x2202}Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
occurs at
![]() $r=1$
. This seems paradoxical from the conventional fluid mechanics viewpoint, because the divergence of the derivative of the flow velocity implies that the viscous stress is not well defined on the boundary. Note that, however, the stress is not determined by the derivative of the flow velocity in a rarefied gas, but is directly related to the VDF. In figure 4, we show the variations of the same macroscopic variables for different values of
$r=1$
. This seems paradoxical from the conventional fluid mechanics viewpoint, because the divergence of the derivative of the flow velocity implies that the viscous stress is not well defined on the boundary. Note that, however, the stress is not determined by the derivative of the flow velocity in a rarefied gas, but is directly related to the VDF. In figure 4, we show the variations of the same macroscopic variables for different values of
![]() $\unicode[STIX]{x1D6FC}$
in the case of the Maxwell boundary condition for
$\unicode[STIX]{x1D6FC}$
in the case of the Maxwell boundary condition for
![]() $k=10$
(
$k=10$
(
![]() $Pr=1$
). Again, we see the occurrence of the gradient divergence of the macroscopic variables on the boundary, implying that this phenomenon is not restricted to the case of the diffuse reflection boundary condition. In figure 4(b), several results based on different lattice systems, (M1)–(M3), are shown for
$Pr=1$
). Again, we see the occurrence of the gradient divergence of the macroscopic variables on the boundary, implying that this phenomenon is not restricted to the case of the diffuse reflection boundary condition. In figure 4(b), several results based on different lattice systems, (M1)–(M3), are shown for
![]() $\unicode[STIX]{x1D6FC}=0.2$
((M1) is the finest and (M3) is the coarsest). When the mesh near
$\unicode[STIX]{x1D6FC}=0.2$
((M1) is the finest and (M3) is the coarsest). When the mesh near
![]() $r=1$
is refined, the variation tends to follow that of
$r=1$
is refined, the variation tends to follow that of
![]() $s^{1/2}$
. The cause of the gradient divergence is due to the propagation of the discontinuity of the VDF in the gas. We will come back to this point later in § 6. For the moment, we continue to present our numerical results.
$s^{1/2}$
. The cause of the gradient divergence is due to the propagation of the discontinuity of the VDF in the gas. We will come back to this point later in § 6. For the moment, we continue to present our numerical results.

Figure 3. Variations of
![]() $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
![]() $Q_{\unicode[STIX]{x1D711}}$
near the surface of the sphere as functions of the normal distance
$Q_{\unicode[STIX]{x1D711}}$
near the surface of the sphere as functions of the normal distance
![]() $s=r-1$
for various
$s=r-1$
for various
![]() $k$
(
$k$
(
![]() $Pr=1$
,
$Pr=1$
,
![]() $\unicode[STIX]{x1D6FC}=1$
): (a)
$\unicode[STIX]{x1D6FC}=1$
): (a)
![]() $u_{\unicode[STIX]{x1D711}}$
, (b)
$u_{\unicode[STIX]{x1D711}}$
, (b)
![]() $Q_{\unicode[STIX]{x1D711}}$
.
$Q_{\unicode[STIX]{x1D711}}$
.
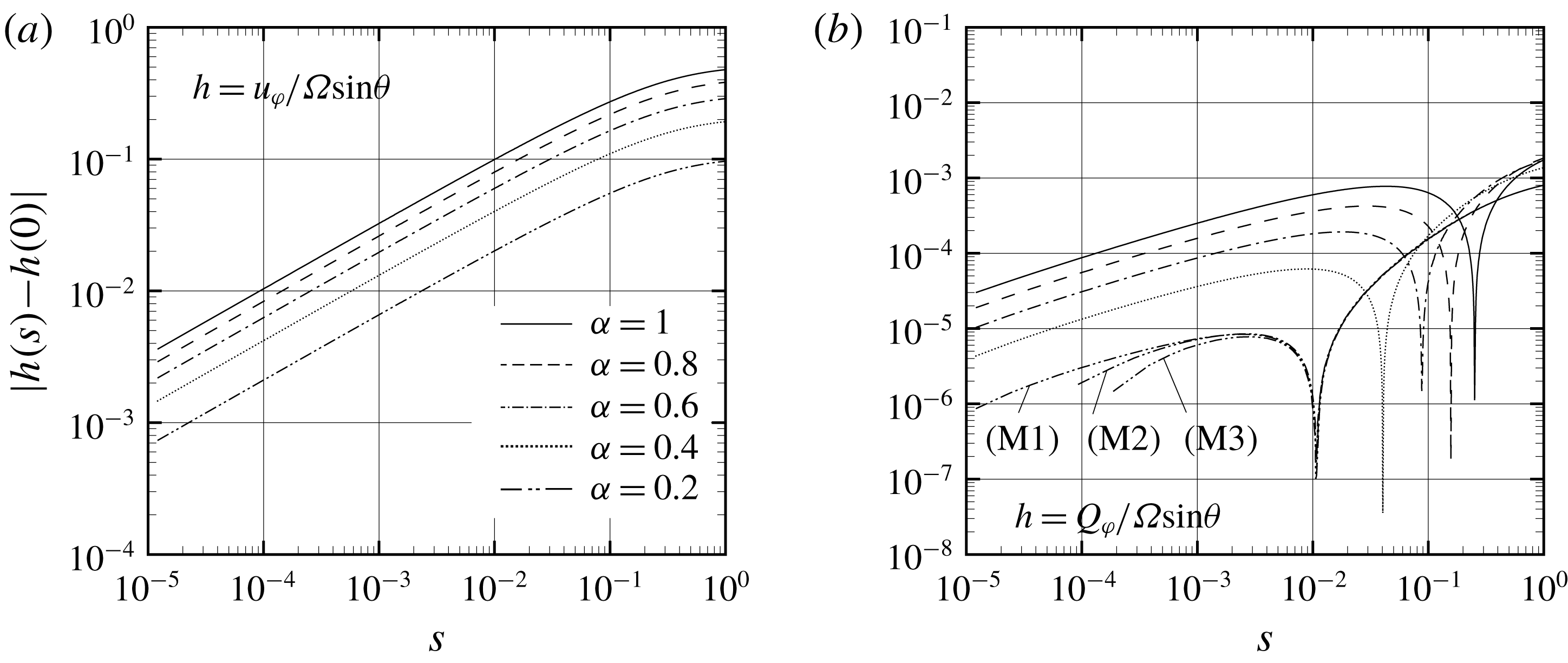
Figure 4. Variations of
![]() $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
![]() $Q_{\unicode[STIX]{x1D711}}$
near the surface of the sphere as functions of the normal distance
$Q_{\unicode[STIX]{x1D711}}$
near the surface of the sphere as functions of the normal distance
![]() $s=r-1$
for various
$s=r-1$
for various
![]() $\unicode[STIX]{x1D6FC}$
(
$\unicode[STIX]{x1D6FC}$
(
![]() $Pr=1$
,
$Pr=1$
,
![]() $k=10$
): (a)
$k=10$
): (a)
![]() $u_{\unicode[STIX]{x1D711}}$
, (b)
$u_{\unicode[STIX]{x1D711}}$
, (b)
![]() $Q_{\unicode[STIX]{x1D711}}$
. (M1)–(M3) in (b) are the results based on different lattice systems; (M1) is the finest and (M3) is the coarsest.
$Q_{\unicode[STIX]{x1D711}}$
. (M1)–(M3) in (b) are the results based on different lattice systems; (M1) is the finest and (M3) is the coarsest.
5.2 Moment of force acting on the sphere
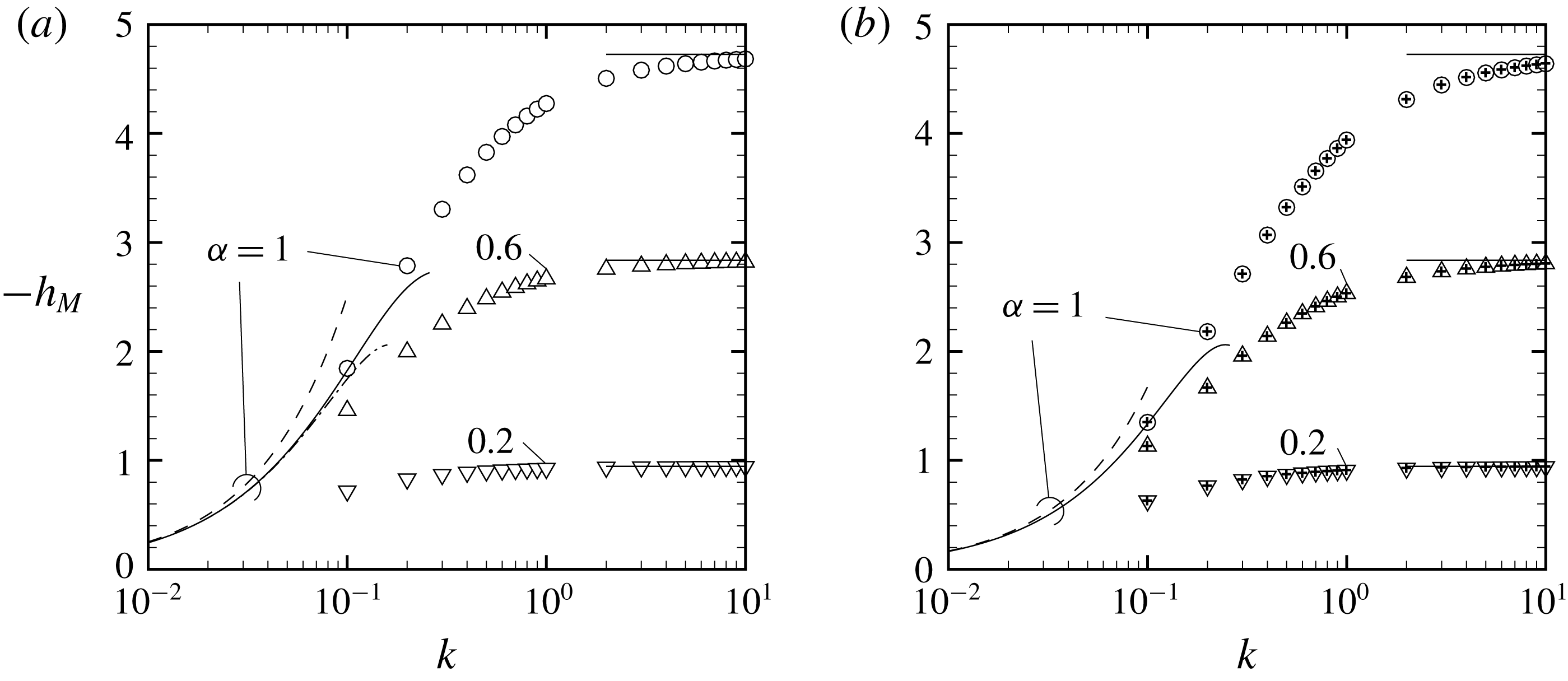
Figure 5. Plots of
![]() $h_{M}$
versus
$h_{M}$
versus
![]() $k$
on the basis of the ES model under the Maxwell boundary condition with accommodation coefficient
$k$
on the basis of the ES model under the Maxwell boundary condition with accommodation coefficient
![]() $\unicode[STIX]{x1D6FC}$
: (a)
$\unicode[STIX]{x1D6FC}$
: (a)
![]() $Pr=1$
(or the BGK model), (b)
$Pr=1$
(or the BGK model), (b)
![]() $Pr=2/3$
. The symbol
$Pr=2/3$
. The symbol
![]() $\circ$
indicates the numerical results. The horizontal lines indicate the values in the collisionless gas limit (
$\circ$
indicates the numerical results. The horizontal lines indicate the values in the collisionless gas limit (
![]() $k\rightarrow \infty$
). The results based on the asymptotic formula (4.5) for
$k\rightarrow \infty$
). The results based on the asymptotic formula (4.5) for
![]() $\unicode[STIX]{x1D6FC}=1$
are shown by the dashed line (one term), by the dash-dotted line (two terms) and by the solid line (three terms). In (b), the symbol
$\unicode[STIX]{x1D6FC}=1$
are shown by the dashed line (one term), by the dash-dotted line (two terms) and by the solid line (three terms). In (b), the symbol
![]() $+$
represents the result obtained from that for
$+$
represents the result obtained from that for
![]() $Pr=1$
with the aid of formula (3.12).
$Pr=1$
with the aid of formula (3.12).
Table 2. Values of
![]() $-h_{M}$
for various
$-h_{M}$
for various
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FC}$
on the basis of the BGK model (or the ES model with
$\unicode[STIX]{x1D6FC}$
on the basis of the BGK model (or the ES model with
![]() $Pr=1$
) under the Maxwell boundary condition with accommodation coefficient
$Pr=1$
) under the Maxwell boundary condition with accommodation coefficient
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.
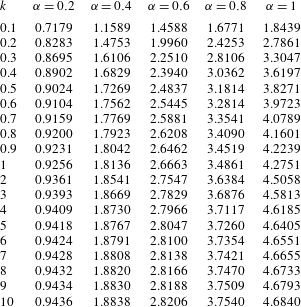
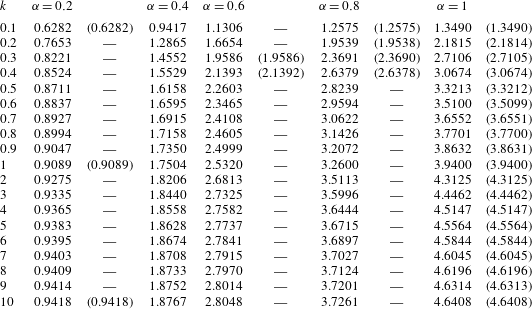
Table 3. Values of
![]() $-h_{M}$
for various
$-h_{M}$
for various
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6FC}$
on the basis of the ES model with
$\unicode[STIX]{x1D6FC}$
on the basis of the ES model with
![]() $Pr=2/3$
under the Maxwell boundary condition with accommodation coefficient
$Pr=2/3$
under the Maxwell boundary condition with accommodation coefficient
![]() $\unicode[STIX]{x1D6FC}$
. The results were obtained from those for
$\unicode[STIX]{x1D6FC}$
. The results were obtained from those for
![]() $Pr=1$
with the aid of formula (3.12). The results of direct numerical computations for
$Pr=1$
with the aid of formula (3.12). The results of direct numerical computations for
![]() $Pr=2/3$
are shown in parentheses.
$Pr=2/3$
are shown in parentheses.
We now show the results for the (dimensionless) moment of force
![]() $h_{M}$
acting on the sphere. Figure 5 shows
$h_{M}$
acting on the sphere. Figure 5 shows
![]() $h_{M}$
as a function of
$h_{M}$
as a function of
![]() $k$
for
$k$
for
![]() $Pr=1$
and
$Pr=1$
and
![]() $2/3$
and for various values of
$2/3$
and for various values of
![]() $\unicode[STIX]{x1D6FC}$
(
$\unicode[STIX]{x1D6FC}$
(
![]() $\unicode[STIX]{x1D6FC}=1$
, 0.6 and 0.2). The symbols represent the results of direct numerical analysis. For comparison, the values of
$\unicode[STIX]{x1D6FC}=1$
, 0.6 and 0.2). The symbols represent the results of direct numerical analysis. For comparison, the values of
![]() $h_{M}$
for
$h_{M}$
for
![]() $Pr=2/3$
are also calculated from those for
$Pr=2/3$
are also calculated from those for
![]() $Pr=1$
with the aid of formula (3.12) and are shown by the symbol
$Pr=1$
with the aid of formula (3.12) and are shown by the symbol
![]() $+$
in figure 5(b). The results of the direct numerical computations and those obtained from the formula agree well (see also table 3). The corresponding values for
$+$
in figure 5(b). The results of the direct numerical computations and those obtained from the formula agree well (see also table 3). The corresponding values for
![]() $Pr=1$
and those for
$Pr=1$
and those for
![]() $Pr=2/3$
are tabulated in tables 2 and 3, respectively, where the results for
$Pr=2/3$
are tabulated in tables 2 and 3, respectively, where the results for
![]() $\unicode[STIX]{x1D6FC}=0.8$
and 0.4 are also included. The magnitude of
$\unicode[STIX]{x1D6FC}=0.8$
and 0.4 are also included. The magnitude of
![]() $h_{M}$
increases monotonically with
$h_{M}$
increases monotonically with
![]() $k$
, and approaches the limiting value
$k$
, and approaches the limiting value
![]() $h_{M}\rightarrow -(8/3)\unicode[STIX]{x03C0}^{1/2}\unicode[STIX]{x1D6FC}$
as
$h_{M}\rightarrow -(8/3)\unicode[STIX]{x03C0}^{1/2}\unicode[STIX]{x1D6FC}$
as
![]() $k\rightarrow \infty$
. The moment of force decreases in its magnitude with the decrease of the accommodation coefficient
$k\rightarrow \infty$
. The moment of force decreases in its magnitude with the decrease of the accommodation coefficient
![]() $\unicode[STIX]{x1D6FC}$
. The two-term asymptotic formula and three-term formula for
$\unicode[STIX]{x1D6FC}$
. The two-term asymptotic formula and three-term formula for
![]() $\unicode[STIX]{x1D6FC}=1$
(the dash-dotted line and the solid line) do not make a difference in the case of
$\unicode[STIX]{x1D6FC}=1$
(the dash-dotted line and the solid line) do not make a difference in the case of
![]() $Pr=2/3$
, since the coefficient of the term
$Pr=2/3$
, since the coefficient of the term
![]() $k^{3}$
is zero within the significant figures (see table 1). Incidentally, the asymptotic formula for the Maxwell boundary condition with
$k^{3}$
is zero within the significant figures (see table 1). Incidentally, the asymptotic formula for the Maxwell boundary condition with
![]() $\unicode[STIX]{x1D6FC}\in (0,1)$
requires information on the slip coefficients
$\unicode[STIX]{x1D6FC}\in (0,1)$
requires information on the slip coefficients
![]() $(k_{0},a_{1},a_{2},a_{3})$
for
$(k_{0},a_{1},a_{2},a_{3})$
for
![]() $\unicode[STIX]{x1D6FC}\neq 1$
. The values of the first-order slip coefficient
$\unicode[STIX]{x1D6FC}\neq 1$
. The values of the first-order slip coefficient
![]() $k_{0}$
under the Maxwell boundary condition were obtained by Wakabayashi, Ohwada & Golse (Reference Wakabayashi, Ohwada and Golse1996) for various
$k_{0}$
under the Maxwell boundary condition were obtained by Wakabayashi, Ohwada & Golse (Reference Wakabayashi, Ohwada and Golse1996) for various
![]() $\unicode[STIX]{x1D6FC}$
, for a hard-sphere gas. Results based on the variational approach are available in Loyalka & Hickey (Reference Loyalka and Hickey1989). The leading-order term of the formula is given by
$\unicode[STIX]{x1D6FC}$
, for a hard-sphere gas. Results based on the variational approach are available in Loyalka & Hickey (Reference Loyalka and Hickey1989). The leading-order term of the formula is given by
![]() $h_{M}=-8\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6FC}k$
.
$h_{M}=-8\unicode[STIX]{x03C0}\unicode[STIX]{x1D6FE}_{1}\unicode[STIX]{x1D6FC}k$
.
The increasing trend of
![]() $-h_{M}$
in terms of
$-h_{M}$
in terms of
![]() $k$
can be interpreted in the case of large and small
$k$
can be interpreted in the case of large and small
![]() $k$
as follows. For the sake of convenience of discussion, we take a frame of reference rotating with the sphere, in which the sphere is at rest and the fluid is rotating. Also for clarity, we consider the situation where the molecules are reflected diffusely on the surface. In this case, the reflected molecules have an isotropic velocity distribution and give no contribution to the tangential momentum flux on the surface at a point under consideration. Then, the torque acting on the sphere is determined solely by the tangential momentum flux carried by the impinging molecules on the boundary. For the free molecular flow, all the impinging molecules come directly from infinity. When
$k$
as follows. For the sake of convenience of discussion, we take a frame of reference rotating with the sphere, in which the sphere is at rest and the fluid is rotating. Also for clarity, we consider the situation where the molecules are reflected diffusely on the surface. In this case, the reflected molecules have an isotropic velocity distribution and give no contribution to the tangential momentum flux on the surface at a point under consideration. Then, the torque acting on the sphere is determined solely by the tangential momentum flux carried by the impinging molecules on the boundary. For the free molecular flow, all the impinging molecules come directly from infinity. When
![]() $k$
is large but finite, some molecules, after having been reflected on the surface, collide with the incoming molecules and hit them back, thereby reducing the momentum flux transmitted to the boundary. The torque is therefore reduced with a decrease of
$k$
is large but finite, some molecules, after having been reflected on the surface, collide with the incoming molecules and hit them back, thereby reducing the momentum flux transmitted to the boundary. The torque is therefore reduced with a decrease of
![]() $k$
when
$k$
when
![]() $k$
is large. On the other hand, when
$k$
is large. On the other hand, when
![]() $k$
is small, the molecules coming from the region several mean free paths away from the surface essentially determine the momentum flux. Since there is a shear around the sphere, the molecules arriving at a point on the surface have faster tangential velocity when
$k$
is small, the molecules coming from the region several mean free paths away from the surface essentially determine the momentum flux. Since there is a shear around the sphere, the molecules arriving at a point on the surface have faster tangential velocity when
![]() $k$
becomes larger. Therefore, the torque increases with
$k$
becomes larger. Therefore, the torque increases with
![]() $k$
, when
$k$
, when
![]() $k$
is small.
$k$
is small.
Finally, we compare
![]() $h_{M}$
for different
$h_{M}$
for different
![]() $Pr$
in the case of
$Pr$
in the case of
![]() $\unicode[STIX]{x1D6FC}=1$
(i.e. the diffuse reflection boundary condition) in figure 6. Here, the results for
$\unicode[STIX]{x1D6FC}=1$
(i.e. the diffuse reflection boundary condition) in figure 6. Here, the results for
![]() $Pr>1$
are also included though this is unrealistic for a gas. The value of
$Pr>1$
are also included though this is unrealistic for a gas. The value of
![]() $-h_{M}$
increases with the increase of
$-h_{M}$
increases with the increase of
![]() $Pr$
. However, if
$Pr$
. However, if
![]() $Pr$
is further increased, the monotonicity of
$Pr$
is further increased, the monotonicity of
![]() $-h_{M}$
with respect to
$-h_{M}$
with respect to
![]() $k$
is lost.
$k$
is lost.
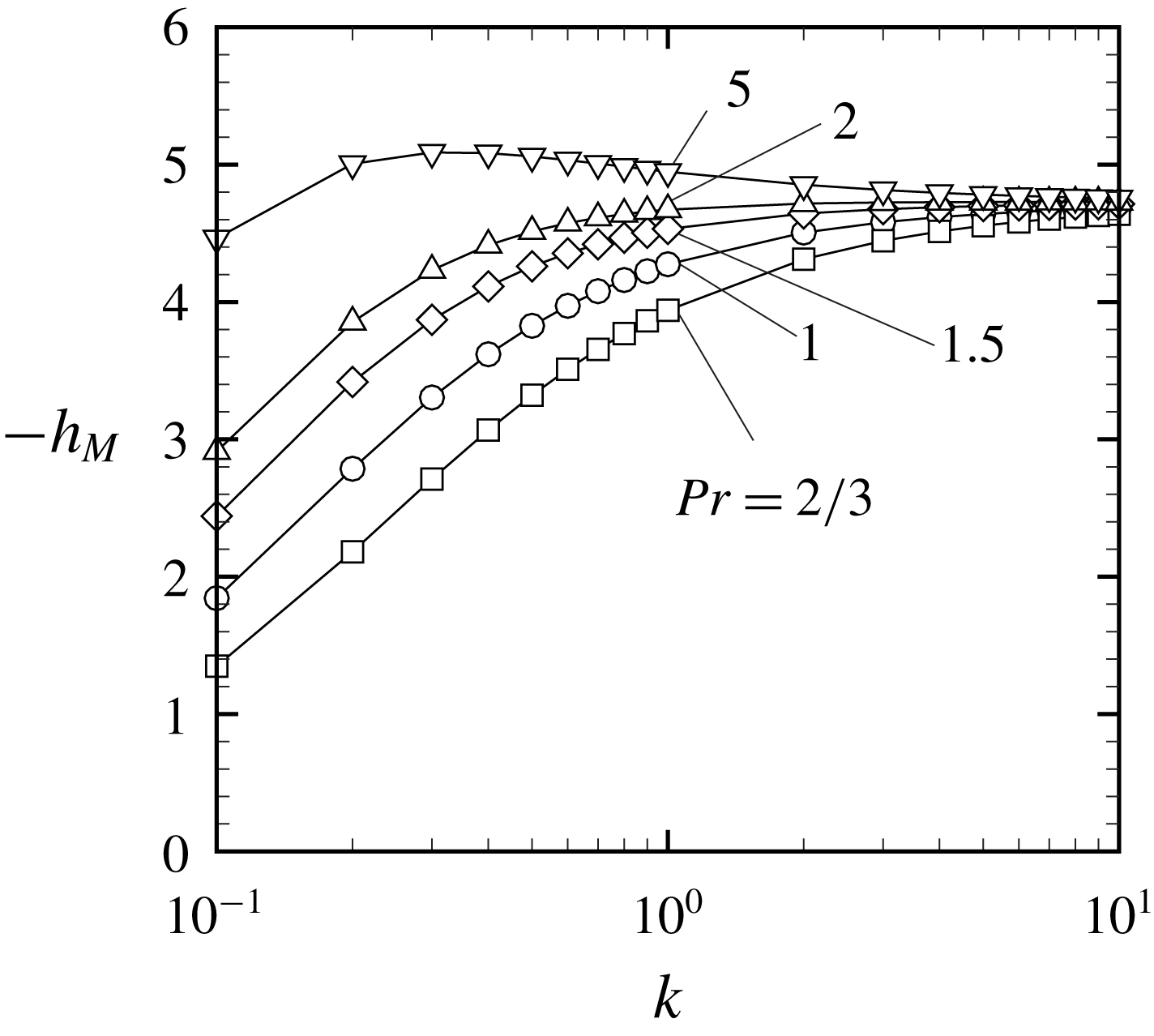
Figure 6. Plots of
![]() $h_{M}$
versus
$h_{M}$
versus
![]() $k$
for various
$k$
for various
![]() $Pr$
in the case of
$Pr$
in the case of
![]() $\unicode[STIX]{x1D6FC}=1$
(the diffuse reflection condition). The symbols show the numerical results based on the ES model, which are connected by solid lines.
$\unicode[STIX]{x1D6FC}=1$
(the diffuse reflection condition). The symbols show the numerical results based on the ES model, which are connected by solid lines.
Remark 1. We have so far confined our consideration to the case of a monatomic gas. The extension to the case of a polyatomic gas is simple if we adopt the ES model for a polyatomic gas proposed by Andries et al. (Reference Andries, Tallec, Perlat and Perthame2000) to replace our basic equation (with a suitable modification in the diffuse reflection boundary condition). Let us denote by
![]() $\unicode[STIX]{x1D6FF}$
the number of internal degrees of freedom of a gas molecule, by
$\unicode[STIX]{x1D6FF}$
the number of internal degrees of freedom of a gas molecule, by
![]() $RT_{\infty }\unicode[STIX]{x1D716}$
the energy related to the internal degrees of freedom and by
$RT_{\infty }\unicode[STIX]{x1D716}$
the energy related to the internal degrees of freedom and by
![]() $\unicode[STIX]{x1D70C}_{\infty }(2RT_{\infty })^{-3/2}(RT_{\infty })^{-1}(1+\overline{\unicode[STIX]{x1D719}}(\boldsymbol{x},\unicode[STIX]{x1D73B},\unicode[STIX]{x1D716}))E(\unicode[STIX]{x1D701}_{i})E_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D716})$
the molecular VDF, where
$\unicode[STIX]{x1D70C}_{\infty }(2RT_{\infty })^{-3/2}(RT_{\infty })^{-1}(1+\overline{\unicode[STIX]{x1D719}}(\boldsymbol{x},\unicode[STIX]{x1D73B},\unicode[STIX]{x1D716}))E(\unicode[STIX]{x1D701}_{i})E_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D716})$
the molecular VDF, where
![]() $E_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D6FF}/2-1}\exp (-\unicode[STIX]{x1D716})$
with
$E_{\unicode[STIX]{x1D6FF}}(\unicode[STIX]{x1D716})=\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FF}}\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D6FF}/2-1}\exp (-\unicode[STIX]{x1D716})$
with
![]() $\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FF}}^{-1}=\int _{0}^{\infty }\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D6FF}/2-1}\exp (-\unicode[STIX]{x1D716})\,\text{d}\unicode[STIX]{x1D716}$
. We also introduce the following notations for the polyatomic gas under consideration:
$\unicode[STIX]{x1D6EC}_{\unicode[STIX]{x1D6FF}}^{-1}=\int _{0}^{\infty }\unicode[STIX]{x1D716}^{\unicode[STIX]{x1D6FF}/2-1}\exp (-\unicode[STIX]{x1D716})\,\text{d}\unicode[STIX]{x1D716}$
. We also introduce the following notations for the polyatomic gas under consideration:
![]() $\ell _{\infty }^{\ast }=(2/\sqrt{\unicode[STIX]{x03C0}})(2RT_{\infty })^{1/2}/A_{c}^{\ast }\unicode[STIX]{x1D70C}_{\infty }$
with
$\ell _{\infty }^{\ast }=(2/\sqrt{\unicode[STIX]{x03C0}})(2RT_{\infty })^{1/2}/A_{c}^{\ast }\unicode[STIX]{x1D70C}_{\infty }$
with
![]() $A_{c}^{\ast }$
being a constant is the molecular mean free path at the reference equilibrium state at rest,
$A_{c}^{\ast }$
being a constant is the molecular mean free path at the reference equilibrium state at rest,
![]() $Kn^{\ast }=\ell _{\infty }^{\ast }/L$
,
$Kn^{\ast }=\ell _{\infty }^{\ast }/L$
,
![]() $k^{\ast }=(\sqrt{\unicode[STIX]{x03C0}}/2)Kn^{\ast }$
,
$k^{\ast }=(\sqrt{\unicode[STIX]{x03C0}}/2)Kn^{\ast }$
,
![]() $\unicode[STIX]{x1D6FC}^{\ast }\in [0,1]$
is the accommodation coefficient (for the present linearised problem, the Maxwell boundary condition on the sphere is given by
$\unicode[STIX]{x1D6FC}^{\ast }\in [0,1]$
is the accommodation coefficient (for the present linearised problem, the Maxwell boundary condition on the sphere is given by
![]() $\overline{\unicode[STIX]{x1D719}}=(1-\unicode[STIX]{x1D6FC}^{\ast })\overline{\unicode[STIX]{x1D719}}(x_{i},\unicode[STIX]{x1D701}_{i}-2\unicode[STIX]{x1D701}_{r}n_{i},\unicode[STIX]{x1D716})+\unicode[STIX]{x1D6FC}^{\ast }(-2\sqrt{\unicode[STIX]{x03C0}}\int _{\unicode[STIX]{x1D701}_{r}<0}\int _{0}^{\infty }\unicode[STIX]{x1D701}_{r}\overline{\unicode[STIX]{x1D719}}EE_{\unicode[STIX]{x1D6FF}}\,\text{d}\unicode[STIX]{x1D716}\,\text{d}\unicode[STIX]{x1D73B}+2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}),\unicode[STIX]{x1D701}_{r}>0,(r=1)$
) and
$\overline{\unicode[STIX]{x1D719}}=(1-\unicode[STIX]{x1D6FC}^{\ast })\overline{\unicode[STIX]{x1D719}}(x_{i},\unicode[STIX]{x1D701}_{i}-2\unicode[STIX]{x1D701}_{r}n_{i},\unicode[STIX]{x1D716})+\unicode[STIX]{x1D6FC}^{\ast }(-2\sqrt{\unicode[STIX]{x03C0}}\int _{\unicode[STIX]{x1D701}_{r}<0}\int _{0}^{\infty }\unicode[STIX]{x1D701}_{r}\overline{\unicode[STIX]{x1D719}}EE_{\unicode[STIX]{x1D6FF}}\,\text{d}\unicode[STIX]{x1D716}\,\text{d}\unicode[STIX]{x1D73B}+2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}),\unicode[STIX]{x1D701}_{r}>0,(r=1)$
) and
is the Prandtl number, where
![]() $\unicode[STIX]{x1D707}_{\infty }^{\ast }$
and
$\unicode[STIX]{x1D707}_{\infty }^{\ast }$
and
![]() $\unicode[STIX]{x1D706}_{\infty }^{\ast }$
are, respectively, the viscosity and the thermal conductivity at the reference state. Then, if we introduce the similarity solution similar to (2.14) as well as its marginal with respect to the energy related to the internal degree of freedom, i.e.
$\unicode[STIX]{x1D706}_{\infty }^{\ast }$
are, respectively, the viscosity and the thermal conductivity at the reference state. Then, if we introduce the similarity solution similar to (2.14) as well as its marginal with respect to the energy related to the internal degree of freedom, i.e.
it turns out that
![]() ${\mathcal{F}}_{S}$
solves the same equation and boundary conditions as
${\mathcal{F}}_{S}$
solves the same equation and boundary conditions as
![]() $\unicode[STIX]{x1D719}_{S}$
, (2.15)–(2.19), provided that the following correspondence between the parameters is satisfied:
$\unicode[STIX]{x1D719}_{S}$
, (2.15)–(2.19), provided that the following correspondence between the parameters is satisfied:
Under the same condition, the macroscopic variables of the polyatomic gas also coincide with those of a monatomic gas. Therefore, the present result for a monatomic gas also gives the result for the case of a polyatomic gas. This also signifies the utility of the conversion formula derived in § 3.
We conclude this section by a brief summary of the present numerical analysis.
(i) The flow speed is faster for
 $Pr=2/3$
than for
$Pr=2/3$
than for
 $Pr=1$
and faster for smaller
$Pr=1$
and faster for smaller
 $k$
.
$k$
.(ii) There exists non-zero heat flux in the gas in spite that the temperature of the gas is uniform. The heat flow vanishes at the two limits
 $k=\infty$
and 0.
$k=\infty$
and 0.(iii) The flow and heat flow decrease as the accommodation coefficient (
 $\unicode[STIX]{x1D6FC}$
) becomes small.
$\unicode[STIX]{x1D6FC}$
) becomes small.(iv) The tangential component of the flow velocity and that of the heat flux,
 $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
 $Q_{\unicode[STIX]{x1D711}}$
, vary abruptly near the boundary in a way that their normal derivatives diverge on the boundary with the rate
$Q_{\unicode[STIX]{x1D711}}$
, vary abruptly near the boundary in a way that their normal derivatives diverge on the boundary with the rate
 $(r-1)^{-1/2}$
. On the other hand, as (2.24) implies, such a divergence of the normal derivative does not occur for
$(r-1)^{-1/2}$
. On the other hand, as (2.24) implies, such a divergence of the normal derivative does not occur for
 $P_{r\unicode[STIX]{x1D711}}$
. Such observations are not peculiar to the diffuse reflection boundary condition.
$P_{r\unicode[STIX]{x1D711}}$
. Such observations are not peculiar to the diffuse reflection boundary condition.(v) Magnitude of dimensionless torque
 $-h_{M}({\geqslant}0)$
is monotonically increasing in
$-h_{M}({\geqslant}0)$
is monotonically increasing in
 $k$
if
$k$
if
 $Pr$
is not very large.
$Pr$
is not very large.(vi) The present result is also applicable to the case of a polyatomic gas.
6 Discussions: gradient divergence
We have seen that the normal derivatives of the macroscopic quantities
![]() $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
![]() $Q_{\unicode[STIX]{x1D711}}$
diverge on the boundary. The present section discusses the cause of the occurrence of gradient divergence in more detail along the line of Takata & Taguchi (Reference Takata and Taguchi2017). The point is the propagation of the discontinuity of the VDF along the characteristics
$Q_{\unicode[STIX]{x1D711}}$
diverge on the boundary. The present section discusses the cause of the occurrence of gradient divergence in more detail along the line of Takata & Taguchi (Reference Takata and Taguchi2017). The point is the propagation of the discontinuity of the VDF along the characteristics
![]() $r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=1$
in the phase space.
$r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=1$
in the phase space.
Let us consider the tangential flow velocity
![]() $u_{\unicode[STIX]{x1D711}}$
as an example, whose radial dependency
$u_{\unicode[STIX]{x1D711}}$
as an example, whose radial dependency
![]() $\widetilde{u}_{\unicode[STIX]{x1D711}}(r)(=u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703})$
is given by
$\widetilde{u}_{\unicode[STIX]{x1D711}}(r)(=u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x1D6FA}\sin \unicode[STIX]{x1D703})$
is given by
Here,
![]() $\unicode[STIX]{x1D719}_{S}$
is regarded as a function of
$\unicode[STIX]{x1D719}_{S}$
is regarded as a function of
![]() $(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})$
. Now, keeping in mind that
$(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})$
. Now, keeping in mind that
![]() $\unicode[STIX]{x1D719}_{S}$
is discontinuous at
$\unicode[STIX]{x1D719}_{S}$
is discontinuous at
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }\equiv \text{Arcsin}(r^{-1})$
, we differentiate the above expression with respect to
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }\equiv \text{Arcsin}(r^{-1})$
, we differentiate the above expression with respect to
![]() $r$
to obtain
$r$
to obtain
where
The second term arises because the location of the discontinuity
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }(r)$
changes with
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }(r)$
changes with
![]() $r$
. Now substituting the explicit form of
$r$
. Now substituting the explicit form of
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }$
, the second term is further transformed into
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }$
, the second term is further transformed into
which diverges with the rate
![]() $(r-1)^{-1/2}$
as
$(r-1)^{-1/2}$
as
![]() $r\downarrow 1$
, provided that
$r\downarrow 1$
, provided that
![]() $|\int _{0}^{\infty }\unicode[STIX]{x1D701}^{4}[\unicode[STIX]{x1D719}_{S}]^{\pm }E\,\text{d}\unicode[STIX]{x1D701}|$
is bounded from below by a positive constant. On the other hand, the first term diverges at most logarithmically on approaching the boundary. We leave the estimate of the first term in appendix B. Thus, the normal derivative
$|\int _{0}^{\infty }\unicode[STIX]{x1D701}^{4}[\unicode[STIX]{x1D719}_{S}]^{\pm }E\,\text{d}\unicode[STIX]{x1D701}|$
is bounded from below by a positive constant. On the other hand, the first term diverges at most logarithmically on approaching the boundary. We leave the estimate of the first term in appendix B. Thus, the normal derivative
![]() $\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
diverges on the boundary with the diverging rate
$\unicode[STIX]{x2202}u_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
diverges on the boundary with the diverging rate
![]() $(r-1)^{-1/2}$
due to the second term of (6.2). Since its mechanism is the propagation of the discontinuity of the VDF into the gas, it should be observed irrespective of the magnitude of
$(r-1)^{-1/2}$
due to the second term of (6.2). Since its mechanism is the propagation of the discontinuity of the VDF into the gas, it should be observed irrespective of the magnitude of
![]() $k$
(even in the free molecular gas limit). Similarly, we can show that
$k$
(even in the free molecular gas limit). Similarly, we can show that
![]() $\unicode[STIX]{x2202}Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
diverges with the same rate,
$\unicode[STIX]{x2202}Q_{\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
diverges with the same rate,
![]() $(r-1)^{-1/2}$
, as
$(r-1)^{-1/2}$
, as
![]() $r\downarrow 1$
, which is also consistent with our numerical results.
$r\downarrow 1$
, which is also consistent with our numerical results.
Now let us introduce the following notation for the integral measuring the magnitude of jump across
![]() $r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=1$
(a weighted marginal with respect to the
$r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=1$
(a weighted marginal with respect to the
![]() $\unicode[STIX]{x1D701}$
-variable):
$\unicode[STIX]{x1D701}$
-variable):
From the above discussion,
![]() $\widetilde{u}_{\unicode[STIX]{x1D711}}$
can be expressed as
$\widetilde{u}_{\unicode[STIX]{x1D711}}$
can be expressed as
![]() $\widetilde{u}_{\unicode[STIX]{x1D711}}=\widetilde{u}_{\unicode[STIX]{x1D711}}|_{r=1}+C_{1}(r-1)^{1/2}+\cdots$
for
$\widetilde{u}_{\unicode[STIX]{x1D711}}=\widetilde{u}_{\unicode[STIX]{x1D711}}|_{r=1}+C_{1}(r-1)^{1/2}+\cdots$
for
![]() $r\sim 1$
, and the coefficient
$r\sim 1$
, and the coefficient
![]() $C_{1}$
of the leading term of the diverging gradient should be related to
$C_{1}$
of the leading term of the diverging gradient should be related to
![]() $G_{0}\equiv \lim _{r\rightarrow 1+0}G(r)$
as
$G_{0}\equiv \lim _{r\rightarrow 1+0}G(r)$
as
where the factor
![]() $2^{1/2}\unicode[STIX]{x03C0}$
is purely geometric. To check this relation, the value of
$2^{1/2}\unicode[STIX]{x03C0}$
is purely geometric. To check this relation, the value of
![]() $C_{1}$
was obtained by fitting the curve
$C_{1}$
was obtained by fitting the curve
![]() $\widetilde{u}_{\unicode[STIX]{x1D711}}=\widetilde{u}_{\unicode[STIX]{x1D711}}|_{r=1}+C_{1}(r-1)^{1/2}$
to the numerical data by the least-squares method using five data points adjacent to the boundary. At the same time, the value of
$\widetilde{u}_{\unicode[STIX]{x1D711}}=\widetilde{u}_{\unicode[STIX]{x1D711}}|_{r=1}+C_{1}(r-1)^{1/2}$
to the numerical data by the least-squares method using five data points adjacent to the boundary. At the same time, the value of
![]() $G_{0}(=G(1))$
was calculated numerically using the data of
$G_{0}(=G(1))$
was calculated numerically using the data of
![]() $\unicode[STIX]{x1D719}_{S}$
at
$\unicode[STIX]{x1D719}_{S}$
at
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x03C0}/2\pm 0$
on the boundary. We show the values of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}=\unicode[STIX]{x03C0}/2\pm 0$
on the boundary. We show the values of
![]() $C_{1}$
and
$C_{1}$
and
![]() $G_{0}$
thus obtained in table 4 and in figure 7 for
$G_{0}$
thus obtained in table 4 and in figure 7 for
![]() $k=10$
and 1 and for various
$k=10$
and 1 and for various
![]() $\unicode[STIX]{x1D6FC}$
in the case of
$\unicode[STIX]{x1D6FC}$
in the case of
![]() $Pr=1$
. It is clearly observed that
$Pr=1$
. It is clearly observed that
![]() $C_{1}$
varies in proportion to
$C_{1}$
varies in proportion to
![]() $G_{0}$
, a measure of the magnitude of jump discontinuity of the VDF (see figure 7
b). The constant of proportionality is, according to (6.6),
$G_{0}$
, a measure of the magnitude of jump discontinuity of the VDF (see figure 7
b). The constant of proportionality is, according to (6.6),
![]() $2^{1/2}\unicode[STIX]{x03C0}\sim 4.44288$
irrespective of
$2^{1/2}\unicode[STIX]{x03C0}\sim 4.44288$
irrespective of
![]() $\unicode[STIX]{x1D6FC}>0$
. As is seen from the columns
$\unicode[STIX]{x1D6FC}>0$
. As is seen from the columns
![]() $C_{1}/G_{0}$
in table 4, our numerical results show
$C_{1}/G_{0}$
in table 4, our numerical results show
![]() $C_{1}/G_{0}\sim 4.4$
, which is close to
$C_{1}/G_{0}\sim 4.4$
, which is close to
![]() $2^{1/2}\unicode[STIX]{x03C0}$
, and again support the discussion in this section.
$2^{1/2}\unicode[STIX]{x03C0}$
, and again support the discussion in this section.
Figure 7. (a) Plots of
![]() $C_{1}$
and
$C_{1}$
and
![]() $G_{0}=\lim _{r\downarrow 1}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{4}[\unicode[STIX]{x1D719}_{S}]^{\pm }E\,\text{d}\unicode[STIX]{x1D701}$
for various accommodation coefficients
$G_{0}=\lim _{r\downarrow 1}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{4}[\unicode[STIX]{x1D719}_{S}]^{\pm }E\,\text{d}\unicode[STIX]{x1D701}$
for various accommodation coefficients
![]() $\unicode[STIX]{x1D6FC}$
in the cases of
$\unicode[STIX]{x1D6FC}$
in the cases of
![]() $k=10$
and 1 (
$k=10$
and 1 (
![]() $Pr=1$
). The circles (○, ●) are for the case
$Pr=1$
). The circles (○, ●) are for the case
![]() $k=10$
and the triangles (▵, ▴) for the case
$k=10$
and the triangles (▵, ▴) for the case
![]() $k=1$
. (b) Double-log plot of
$k=1$
. (b) Double-log plot of
![]() $|C_{1}|$
versus
$|C_{1}|$
versus
![]() $|G_{0}|$
for
$|G_{0}|$
for
![]() $k=10$
(○) and 1 (▵). In both panels, the symbols represent the numerical results, which are connected by solid lines.
$k=10$
(○) and 1 (▵). In both panels, the symbols represent the numerical results, which are connected by solid lines.
Table 4. Values of
![]() $C_{1}$
and
$C_{1}$
and
![]() $G_{0}=\lim _{r\downarrow 1}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{4}[\unicode[STIX]{x1D719}_{S}]^{\pm }E\,\text{d}\unicode[STIX]{x1D701}$
for various accommodation coefficients
$G_{0}=\lim _{r\downarrow 1}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{4}[\unicode[STIX]{x1D719}_{S}]^{\pm }E\,\text{d}\unicode[STIX]{x1D701}$
for various accommodation coefficients
![]() $\unicode[STIX]{x1D6FC}$
(
$\unicode[STIX]{x1D6FC}$
(
![]() $k=10,1$
).
$k=10,1$
).
As for
![]() $P_{r\unicode[STIX]{x1D711}}$
, a factor
$P_{r\unicode[STIX]{x1D711}}$
, a factor
![]() $\unicode[STIX]{x1D701}_{r}=\unicode[STIX]{x1D701}\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}$
is contained in the integrand. This factor acts to cancel the singularity originated from
$\unicode[STIX]{x1D701}_{r}=\unicode[STIX]{x1D701}\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}$
is contained in the integrand. This factor acts to cancel the singularity originated from
![]() $\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }/\text{d}r$
as well as that contained in the first term. This explains why
$\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}^{\ast }/\text{d}r$
as well as that contained in the first term. This explains why
![]() $\unicode[STIX]{x2202}P_{r\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
remains finite as
$\unicode[STIX]{x2202}P_{r\unicode[STIX]{x1D711}}/\unicode[STIX]{x2202}r$
remains finite as
![]() $r\downarrow 1$
. This result is also consistent with the more general result that the normal derivative of any moment which contains
$r\downarrow 1$
. This result is also consistent with the more general result that the normal derivative of any moment which contains
![]() $\unicode[STIX]{x1D701}_{i}n_{i}$
as a factor in the integrand (
$\unicode[STIX]{x1D701}_{i}n_{i}$
as a factor in the integrand (
![]() $n_{i}$
is the unit normal vector to the boundary) does not diverge on a smooth boundary (Takata & Taguchi Reference Takata and Taguchi2017).
$n_{i}$
is the unit normal vector to the boundary) does not diverge on a smooth boundary (Takata & Taguchi Reference Takata and Taguchi2017).
We conclude this section with a brief comment on the S layer. The discontinuity of the VDF decays appreciably over the distance of the order of the mean free path due to molecular collisions. Therefore, when
![]() $k$
is small, the region where the discontinuity of the VDF is appreciable is confined in a thin region adjacent to the boundary with a thickness of the order of
$k$
is small, the region where the discontinuity of the VDF is appreciable is confined in a thin region adjacent to the boundary with a thickness of the order of
![]() $Lk^{2}$
. This thin region at the bottom of the Knudsen layer whose thickness is of the order of
$Lk^{2}$
. This thin region at the bottom of the Knudsen layer whose thickness is of the order of
![]() $Lk$
is the S layer (Sone Reference Sone1973; Sone & Takata Reference Sone and Takata1992). The discussion in the present section is applicable irrespective of the values of
$Lk$
is the S layer (Sone Reference Sone1973; Sone & Takata Reference Sone and Takata1992). The discussion in the present section is applicable irrespective of the values of
![]() $k$
, and therefore naturally applies to the S layer. In this way, the present results also clarify the structure of the S layer around a rotating sphere.
$k$
, and therefore naturally applies to the S layer. In this way, the present results also clarify the structure of the S layer around a rotating sphere.
7 Conclusion
In this paper, we have studied in detail a flow induced around a spinning sphere in a rarefied gas, on the basis of the linearised ES model and Maxwell diffuse–specular boundary condition. The main results are summarised as follows:
(i) We have derived a conversion formula that allows us to derive the result for arbitrary
 $Pr$
$Pr$
 $({\geqslant}2/3)$
from that for
$({\geqslant}2/3)$
from that for
 $Pr=1$
, for given
$Pr=1$
, for given
 $(k,\unicode[STIX]{x1D6FC})$
.
$(k,\unicode[STIX]{x1D6FC})$
.(ii) We have clarified the detailed profiles of the macroscopic quantities (flow velocity, tangential stress, heat flow). In particular, we have shown numerically that the normal derivatives of
 $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
 $Q_{\unicode[STIX]{x1D711}}$
diverge on the boundary with the rate
$Q_{\unicode[STIX]{x1D711}}$
diverge on the boundary with the rate
 $1/\sqrt{r-1}$
, which is consistent with the estimate obtained by Takata & Taguchi (Reference Takata and Taguchi2017). The diverging terms in the normal derivatives of
$1/\sqrt{r-1}$
, which is consistent with the estimate obtained by Takata & Taguchi (Reference Takata and Taguchi2017). The diverging terms in the normal derivatives of
 $u_{\unicode[STIX]{x1D711}}$
and
$u_{\unicode[STIX]{x1D711}}$
and
 $Q_{\unicode[STIX]{x1D711}}$
are proportional to the magnitude of the jump discontinuity in the VDF on the boundary.
$Q_{\unicode[STIX]{x1D711}}$
are proportional to the magnitude of the jump discontinuity in the VDF on the boundary.(iii) On the other hand, the normal derivative of
 $P_{r\unicode[STIX]{x1D711}}$
does not diverge on approaching the boundary. This result is consistent with the more general result that the normal derivative of any moment containing
$P_{r\unicode[STIX]{x1D711}}$
does not diverge on approaching the boundary. This result is consistent with the more general result that the normal derivative of any moment containing
 $\unicode[STIX]{x1D701}_{i}n_{i}$
as a factor in the integrand (
$\unicode[STIX]{x1D701}_{i}n_{i}$
as a factor in the integrand (
 $n_{i}$
is the unit normal vector to the boundary) does not diverge on a smooth boundary.
$n_{i}$
is the unit normal vector to the boundary) does not diverge on a smooth boundary.(iv) We have obtained the moment of force acting on the sphere for a wide range of the parameter space.
(v) The present results are also applicable to the case of a polyatomic gas.
Acknowledgements
This work was supported by JSPS KAKENHI grant nos. 25820041 and 17H03173 and in part by JSPS KAKENHI grant no. 17K06146. The authors also acknowledge the support by JSPS and MAEDI under the Japan–France Integrated Action Program (SAKURA).
Appendix A. On the temperature of the sphere
In this paper, we have assumed that the temperature of the sphere is uniform and is equal to that of the gas at infinity. In this appendix, we justify this in the case where the heat flow in the sphere is described by the Fourier law.
We take the linearised Boltzmann equation as our basic equation and assume the general kinetic boundary condition on the sphere, which includes the ES model and the Maxwell boundary condition as particular examples. Let
![]() $\unicode[STIX]{x1D70C}_{\infty }(2RT_{\infty })^{-3/2}(1+\unicode[STIX]{x1D719}(\boldsymbol{x},\unicode[STIX]{x1D73B}))E$
be the VDF of the gas molecules,
$\unicode[STIX]{x1D70C}_{\infty }(2RT_{\infty })^{-3/2}(1+\unicode[STIX]{x1D719}(\boldsymbol{x},\unicode[STIX]{x1D73B}))E$
be the VDF of the gas molecules,
![]() $T_{\infty }(1+\unicode[STIX]{x1D70F}_{s}(\boldsymbol{x}))$
be the temperature of the sphere,
$T_{\infty }(1+\unicode[STIX]{x1D70F}_{s}(\boldsymbol{x}))$
be the temperature of the sphere,
![]() $(2RT_{\infty })^{-3/2}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
be the scattering kernel at the reference equilibrium state at rest describing the relation between the velocities of the incident molecules
$(2RT_{\infty })^{-3/2}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
be the scattering kernel at the reference equilibrium state at rest describing the relation between the velocities of the incident molecules
![]() $\unicode[STIX]{x1D73B}^{\ast }$
(
$\unicode[STIX]{x1D73B}^{\ast }$
(
![]() $\unicode[STIX]{x1D701}_{r}^{\ast }<0$
) and those of the reflected molecules
$\unicode[STIX]{x1D701}_{r}^{\ast }<0$
) and those of the reflected molecules
![]() $\unicode[STIX]{x1D73B}$
(
$\unicode[STIX]{x1D73B}$
(
![]() $\unicode[STIX]{x1D701}_{r}>0$
) on the surface and
$\unicode[STIX]{x1D701}_{r}>0$
) on the surface and
![]() $p_{\infty }(2RT_{\infty })^{1/2}(L/T_{\infty })\hat{\unicode[STIX]{x1D706}}_{s}({>}0)$
be the thermal conductivity of the sphere. The other notations appearing below are the same as those in the main text, unless otherwise stated. Then,
$p_{\infty }(2RT_{\infty })^{1/2}(L/T_{\infty })\hat{\unicode[STIX]{x1D706}}_{s}({>}0)$
be the thermal conductivity of the sphere. The other notations appearing below are the same as those in the main text, unless otherwise stated. Then,
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D70F}_{s}$
satisfy the following equations and boundary conditions:
$\unicode[STIX]{x1D70F}_{s}$
satisfy the following equations and boundary conditions:
and
![]() $\unicode[STIX]{x1D719}^{\ast }$
,
$\unicode[STIX]{x1D719}^{\ast }$
,
![]() $g_{w}^{\ast }$
and
$g_{w}^{\ast }$
and
![]() $E^{\ast }$
are
$E^{\ast }$
are
![]() $\unicode[STIX]{x1D719}^{\ast }=\unicode[STIX]{x1D719}(\boldsymbol{x},\unicode[STIX]{x1D73B}^{\ast })$
,
$\unicode[STIX]{x1D719}^{\ast }=\unicode[STIX]{x1D719}(\boldsymbol{x},\unicode[STIX]{x1D73B}^{\ast })$
,
![]() $g_{w}^{\ast }=g_{w}(\unicode[STIX]{x1D73B}^{\ast })$
and
$g_{w}^{\ast }=g_{w}(\unicode[STIX]{x1D73B}^{\ast })$
and
![]() $E(\unicode[STIX]{x1D73B}^{\ast })$
, respectively. The function
$E(\unicode[STIX]{x1D73B}^{\ast })$
, respectively. The function
![]() $g_{w}$
depends also on the position on the sphere through
$g_{w}$
depends also on the position on the sphere through
![]() $\unicode[STIX]{x1D703}$
and
$\unicode[STIX]{x1D703}$
and
![]() $\unicode[STIX]{x1D70F}_{s}$
. Equation (A 2b
), which states the continuity of heat flow across the surface, is the linearised version of the conservation of energy on the surface (i.e. the continuity of energy flow across the surface).
$\unicode[STIX]{x1D70F}_{s}$
. Equation (A 2b
), which states the continuity of heat flow across the surface, is the linearised version of the conservation of energy on the surface (i.e. the continuity of energy flow across the surface).
The operator
![]() ${\mathcal{L}}$
satisfies the following well-known properties:
${\mathcal{L}}$
satisfies the following well-known properties:
(i)
(A 4) $$\begin{eqnarray}{\mathcal{L}}[\unicode[STIX]{x1D711}]=0\;\Longleftrightarrow \;\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B})~\text{is a linear combination of 1},\unicode[STIX]{x1D73B}~\text{and}~|\unicode[STIX]{x1D73B}|^{2}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{L}}[\unicode[STIX]{x1D711}]=0\;\Longleftrightarrow \;\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B})~\text{is a linear combination of 1},\unicode[STIX]{x1D73B}~\text{and}~|\unicode[STIX]{x1D73B}|^{2}.\end{eqnarray}$$
(ii) For any function
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B})$
, (A 5)and the equality holds if and only if
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B})$
, (A 5)and the equality holds if and only if $$\begin{eqnarray}\langle \unicode[STIX]{x1D711}{\mathcal{L}}[\unicode[STIX]{x1D711}]\rangle \leqslant 0,\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D711}{\mathcal{L}}[\unicode[STIX]{x1D711}]\rangle \leqslant 0,\end{eqnarray}$$
 $\unicode[STIX]{x1D711}$
is a linear combination of 1,
$\unicode[STIX]{x1D711}$
is a linear combination of 1,
 $\unicode[STIX]{x1D73B}$
and
$\unicode[STIX]{x1D73B}$
and
 $|\unicode[STIX]{x1D73B}|^{2}$
.
$|\unicode[STIX]{x1D73B}|^{2}$
.
The scattering kernel
![]() $K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
is required to satisfy the following basic properties. Let
$K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
is required to satisfy the following basic properties. Let
![]() $n_{i}$
be the unit normal vector on the boundary pointing to the gas and let
$n_{i}$
be the unit normal vector on the boundary pointing to the gas and let
![]() $\unicode[STIX]{x1D701}_{n}=\unicode[STIX]{x1D701}_{i}n_{i}$
and
$\unicode[STIX]{x1D701}_{n}=\unicode[STIX]{x1D701}_{i}n_{i}$
and
![]() $\unicode[STIX]{x1D701}_{n}^{\ast }=\unicode[STIX]{x1D701}_{i}^{\ast }n_{i}$
.
$\unicode[STIX]{x1D701}_{n}^{\ast }=\unicode[STIX]{x1D701}_{i}^{\ast }n_{i}$
.
(i) Positivity:
(A 6) $$\begin{eqnarray}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })\geqslant 0,\quad \text{for}~\unicode[STIX]{x1D701}_{n}^{\ast }<0~\text{and}~\unicode[STIX]{x1D701}_{n}>0.\end{eqnarray}$$
$$\begin{eqnarray}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })\geqslant 0,\quad \text{for}~\unicode[STIX]{x1D701}_{n}^{\ast }<0~\text{and}~\unicode[STIX]{x1D701}_{n}>0.\end{eqnarray}$$
(ii) Impermeability:
(A 7) $$\begin{eqnarray}\int _{\unicode[STIX]{x1D701}_{n}>0}\frac{\unicode[STIX]{x1D701}_{n}}{\unicode[STIX]{x1D701}_{n}^{\ast }}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })\,\text{d}\unicode[STIX]{x1D73B}=-1,\quad \unicode[STIX]{x1D701}_{n}^{\ast }<0.\end{eqnarray}$$
$$\begin{eqnarray}\int _{\unicode[STIX]{x1D701}_{n}>0}\frac{\unicode[STIX]{x1D701}_{n}}{\unicode[STIX]{x1D701}_{n}^{\ast }}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })\,\text{d}\unicode[STIX]{x1D73B}=-1,\quad \unicode[STIX]{x1D701}_{n}^{\ast }<0.\end{eqnarray}$$
(iii) Uniqueness: let
 $\unicode[STIX]{x1D711}_{e}=c_{0}+c_{i}\unicode[STIX]{x1D701}_{i}+c_{4}|\unicode[STIX]{x1D73B}|^{2}$
, where
$\unicode[STIX]{x1D711}_{e}=c_{0}+c_{i}\unicode[STIX]{x1D701}_{i}+c_{4}|\unicode[STIX]{x1D73B}|^{2}$
, where
 $c_{0}$
,
$c_{0}$
,
 $c_{i}$
(
$c_{i}$
(
 $i=1,2,3$
) and
$i=1,2,3$
) and
 $c_{4}$
are independent of
$c_{4}$
are independent of
 $\unicode[STIX]{x1D73B}$
. Then, the equality (A 8)holds if and only if
$\unicode[STIX]{x1D73B}$
. Then, the equality (A 8)holds if and only if $$\begin{eqnarray}\unicode[STIX]{x1D711}_{e}E=\int _{\unicode[STIX]{x1D701}_{n}^{\ast }<0}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}_{\ast })\unicode[STIX]{x1D711}_{e}(\unicode[STIX]{x1D73B}^{\ast })E^{\ast }\,\text{d}\unicode[STIX]{x1D73B}^{\ast }\quad (\unicode[STIX]{x1D701}_{n}>0)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D711}_{e}E=\int _{\unicode[STIX]{x1D701}_{n}^{\ast }<0}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}_{\ast })\unicode[STIX]{x1D711}_{e}(\unicode[STIX]{x1D73B}^{\ast })E^{\ast }\,\text{d}\unicode[STIX]{x1D73B}^{\ast }\quad (\unicode[STIX]{x1D701}_{n}>0)\end{eqnarray}$$
 $c_{1}=c_{2}=c_{3}=c_{4}=0$
.
$c_{1}=c_{2}=c_{3}=c_{4}=0$
.
Further, if
![]() $K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
satisfies the above properties, the following inequality holds on the boundary:
$K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
satisfies the above properties, the following inequality holds on the boundary:
(i) Darrozes–Guiraud inequality (Cercignani Reference Cercignani1988; Sone Reference Sone2007). Let
 $F(x)$
be a strictly convex function. Then, for any
$F(x)$
be a strictly convex function. Then, for any
 $\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B})$
satisfying (A 9)the following inequality holds:
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B})$
satisfying (A 9)the following inequality holds: $$\begin{eqnarray}\unicode[STIX]{x1D711}E=\int _{\unicode[STIX]{x1D701}_{n}^{\ast }<0}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B}^{\ast })E^{\ast }\,\text{d}\unicode[STIX]{x1D73B}^{\ast },\quad (\unicode[STIX]{x1D701}_{n}>0),\end{eqnarray}$$
(A 10)The equality sign applies if and only if
$$\begin{eqnarray}\unicode[STIX]{x1D711}E=\int _{\unicode[STIX]{x1D701}_{n}^{\ast }<0}K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })\unicode[STIX]{x1D711}(\unicode[STIX]{x1D73B}^{\ast })E^{\ast }\,\text{d}\unicode[STIX]{x1D73B}^{\ast },\quad (\unicode[STIX]{x1D701}_{n}>0),\end{eqnarray}$$
(A 10)The equality sign applies if and only if $$\begin{eqnarray}\langle \unicode[STIX]{x1D701}_{n}F(\unicode[STIX]{x1D711})\rangle \leqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D701}_{n}F(\unicode[STIX]{x1D711})\rangle \leqslant 0.\end{eqnarray}$$
 $\unicode[STIX]{x1D711}$
is independent of
$\unicode[STIX]{x1D711}$
is independent of
 $\unicode[STIX]{x1D73B}$
.
$\unicode[STIX]{x1D73B}$
.
We first consider a reduced problem for
![]() $\unicode[STIX]{x1D719}$
derived from (A 1a
)–(A 1c
) by setting
$\unicode[STIX]{x1D719}$
derived from (A 1a
)–(A 1c
) by setting
![]() $\unicode[STIX]{x1D70F}_{s}\equiv 0$
in the boundary condition (A 1b
), i.e.
$\unicode[STIX]{x1D70F}_{s}\equiv 0$
in the boundary condition (A 1b
), i.e.
![]() $g_{w}\equiv 2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}$
. The solution to this problem is denoted by
$g_{w}\equiv 2\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}$
. The solution to this problem is denoted by
![]() $\unicode[STIX]{x1D719}^{0}$
. Clearly, this corresponds to the situation considered in the main text; the temperature of the sphere is uniform and coincides with that of the gas at infinity. If the scattering operator defined by the kernel
$\unicode[STIX]{x1D719}^{0}$
. Clearly, this corresponds to the situation considered in the main text; the temperature of the sphere is uniform and coincides with that of the gas at infinity. If the scattering operator defined by the kernel
![]() $K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
admits an axial symmetry about the axis normal to the boundary, the same similarity solution of the form (2.14) is applicable, and, consequently, the heat flux across the boundary vanishes since
$K_{B0}(\unicode[STIX]{x1D73B},\unicode[STIX]{x1D73B}^{\ast })$
admits an axial symmetry about the axis normal to the boundary, the same similarity solution of the form (2.14) is applicable, and, consequently, the heat flux across the boundary vanishes since
![]() $Q_{r}[\unicode[STIX]{x1D719}^{0}]=0$
(see the line following (2.20)). Consequently,
$Q_{r}[\unicode[STIX]{x1D719}^{0}]=0$
(see the line following (2.20)). Consequently,
![]() $\unicode[STIX]{x1D70F}_{s}=0$
is a solution to the problem (A 2a
) and (A 2b
) (with
$\unicode[STIX]{x1D70F}_{s}=0$
is a solution to the problem (A 2a
) and (A 2b
) (with
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}^{0}$
). Thus, we conclude that
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D719}^{0}$
). Thus, we conclude that
![]() $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F}_{s})=(\unicode[STIX]{x1D719}^{0},0)$
is a solution to the (full) boundary-value problem (A 1a
)–(A 2b
). Moreover, the uniqueness of the solution (see below) ensures that
$(\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F}_{s})=(\unicode[STIX]{x1D719}^{0},0)$
is a solution to the (full) boundary-value problem (A 1a
)–(A 2b
). Moreover, the uniqueness of the solution (see below) ensures that
![]() $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F}_{s})=(\unicode[STIX]{x1D719}^{0},0)$
is the only solution to the problem (A 1a
)–(A 2b
).
$(\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F}_{s})=(\unicode[STIX]{x1D719}^{0},0)$
is the only solution to the problem (A 1a
)–(A 2b
).
The uniqueness of the solution can be shown along the same line as that of the boundary-value problem of the linearised Boltzmann equation (without the stationary heat-conduction equation) (see e.g. Sone Reference Sone2007, A.12). However, the inclusion of the heat-conduction equation results in an interesting application of the uniqueness condition for the scattering kernel, which is illustrative. Therefore, we present a proof here.
Our goal is to show that the solution to the problem (A 1a
)–(A 1c
) with
![]() $\unicode[STIX]{x1D6FA}=0$
vanishes identically, i.e.
$\unicode[STIX]{x1D6FA}=0$
vanishes identically, i.e.
![]() $(\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F}_{s})=(0,0)$
. To see this, we multiply equation (A 1a
) by
$(\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F}_{s})=(0,0)$
. To see this, we multiply equation (A 1a
) by
![]() $2\unicode[STIX]{x1D719}E$
and integrate the result with respect to
$2\unicode[STIX]{x1D719}E$
and integrate the result with respect to
![]() $\unicode[STIX]{x1D701}_{i}$
over the whole space to obtain
$\unicode[STIX]{x1D701}_{i}$
over the whole space to obtain
(Since the VDF contains discontinuities, the order of spatial derivative and integration cannot be interchanged freely. However, using the fact that the discontinuity of
![]() $\unicode[STIX]{x1D719}$
lies on the characteristics of the equation, one can show that the expression of the most left-hand side of (A 11) is legitimate (Sone Reference Sone2007). The same applies to the sentence containing (2.24).) Further integration with respect to
$\unicode[STIX]{x1D719}$
lies on the characteristics of the equation, one can show that the expression of the most left-hand side of (A 11) is legitimate (Sone Reference Sone2007). The same applies to the sentence containing (2.24).) Further integration with respect to
![]() $\boldsymbol{x}$
over the whole gas region gives
$\boldsymbol{x}$
over the whole gas region gives
Applying Gauss’s divergence theorem on the left-hand side yields
where
![]() $\text{d}S$
is the surface element. Noting that
$\text{d}S$
is the surface element. Noting that
![]() $\langle \unicode[STIX]{x1D701}_{i}\unicode[STIX]{x1D719}^{2}\rangle =O(|\boldsymbol{x}|^{-3})$
for
$\langle \unicode[STIX]{x1D701}_{i}\unicode[STIX]{x1D719}^{2}\rangle =O(|\boldsymbol{x}|^{-3})$
for
![]() $|\boldsymbol{x}|\gg 1$
(this follows from the estimate
$|\boldsymbol{x}|\gg 1$
(this follows from the estimate
![]() $\unicode[STIX]{x1D719}=2\unicode[STIX]{x1D701}_{i}h_{i}+(|\unicode[STIX]{x1D73B}|^{2}-5/2)h_{4}+O(|\boldsymbol{x}|^{-2})$
for
$\unicode[STIX]{x1D719}=2\unicode[STIX]{x1D701}_{i}h_{i}+(|\unicode[STIX]{x1D73B}|^{2}-5/2)h_{4}+O(|\boldsymbol{x}|^{-2})$
for
![]() $|\boldsymbol{x}|\gg 1$
, where
$|\boldsymbol{x}|\gg 1$
, where
![]() $h_{i}$
(
$h_{i}$
(
![]() $i=1,2,3$
) and
$i=1,2,3$
) and
![]() $h_{4}$
, independent of
$h_{4}$
, independent of
![]() $\unicode[STIX]{x1D73B}$
, are quantities of
$\unicode[STIX]{x1D73B}$
, are quantities of
![]() $O(|\boldsymbol{x}|^{-1})$
), the first term on the right-hand side vanishes and (A 12) reduces to
$O(|\boldsymbol{x}|^{-1})$
), the first term on the right-hand side vanishes and (A 12) reduces to
Now if we put
![]() $F(x)=x^{2}$
,
$F(x)=x^{2}$
,
![]() $\unicode[STIX]{x1D711}=\unicode[STIX]{x1D719}-\bar{g}_{w}$
and
$\unicode[STIX]{x1D711}=\unicode[STIX]{x1D719}-\bar{g}_{w}$
and
![]() $\bar{g}_{w}=(|\unicode[STIX]{x1D73B}|^{2}-5/2)\unicode[STIX]{x1D70F}_{s}$
in the Darrozes–Guiraud inequality, the condition (A 9) is satisfied and we have
$\bar{g}_{w}=(|\unicode[STIX]{x1D73B}|^{2}-5/2)\unicode[STIX]{x1D70F}_{s}$
in the Darrozes–Guiraud inequality, the condition (A 9) is satisfied and we have
Since
![]() $\langle \unicode[STIX]{x1D701}_{r}\bar{g}_{w}^{2}\rangle =0$
, the left-hand side is transformed to
$\langle \unicode[STIX]{x1D701}_{r}\bar{g}_{w}^{2}\rangle =0$
, the left-hand side is transformed to
Thus,
Combining this with (A 14), we obtain
On the other hand, multiplying (A 2a
) by
![]() $\unicode[STIX]{x1D70F}_{s}$
and integrating the result inside the sphere gives
$\unicode[STIX]{x1D70F}_{s}$
and integrating the result inside the sphere gives
Applying Gauss’s divergence theorem to the first term gives
where (A 2b ) has been used in the last equality. Therefore,
Hence, from (A 18) and (A 21), we have
Thus,
![]() $\unicode[STIX]{x1D70F}_{s}$
is a constant independent of
$\unicode[STIX]{x1D70F}_{s}$
is a constant independent of
![]() $\boldsymbol{x}$
. Also from (A 14), (A 17) and (A 22),
$\boldsymbol{x}$
. Also from (A 14), (A 17) and (A 22),
In the meantime, since
![]() $\langle \unicode[STIX]{x1D719}{\mathcal{L}}[\unicode[STIX]{x1D719}]\rangle$
is non-positive (see (A 5)),
$\langle \unicode[STIX]{x1D719}{\mathcal{L}}[\unicode[STIX]{x1D719}]\rangle$
is non-positive (see (A 5)),
![]() $\langle \unicode[STIX]{x1D719}{\mathcal{L}}[\unicode[STIX]{x1D719}]\rangle =0$
must hold throughout the gas region. This shows that
$\langle \unicode[STIX]{x1D719}{\mathcal{L}}[\unicode[STIX]{x1D719}]\rangle =0$
must hold throughout the gas region. This shows that
![]() $\unicode[STIX]{x1D719}$
is a linear combination of 1,
$\unicode[STIX]{x1D719}$
is a linear combination of 1,
![]() $\unicode[STIX]{x1D73B}$
and
$\unicode[STIX]{x1D73B}$
and
![]() $|\unicode[STIX]{x1D73B}|^{2}$
. As the result,
$|\unicode[STIX]{x1D73B}|^{2}$
. As the result,
![]() ${\mathcal{L}}[\unicode[STIX]{x1D719}]=0$
holds and (A 1) reduces to
${\mathcal{L}}[\unicode[STIX]{x1D719}]=0$
holds and (A 1) reduces to
Therefore,
![]() $\unicode[STIX]{x1D719}$
is invariant along the characteristics, which implies that
$\unicode[STIX]{x1D719}$
is invariant along the characteristics, which implies that
![]() $\unicode[STIX]{x1D719}=0$
for
$\unicode[STIX]{x1D719}=0$
for
![]() $\unicode[STIX]{x1D701}_{i}$
whose corresponding characteristic can be traced back to infinity. In particular,
$\unicode[STIX]{x1D701}_{i}$
whose corresponding characteristic can be traced back to infinity. In particular,
![]() $\unicode[STIX]{x1D719}=0$
for the incident molecules (
$\unicode[STIX]{x1D719}=0$
for the incident molecules (
![]() $\unicode[STIX]{x1D701}_{r}<0$
) on the boundary (
$\unicode[STIX]{x1D701}_{r}<0$
) on the boundary (
![]() $|\boldsymbol{x}|=1$
). With this, (A 23) is rewritten to give
$|\boldsymbol{x}|=1$
). With this, (A 23) is rewritten to give
which shows that
![]() $\unicode[STIX]{x1D719}=0$
holds also for the outgoing molecules (
$\unicode[STIX]{x1D719}=0$
holds also for the outgoing molecules (
![]() $\unicode[STIX]{x1D701}_{r}>0$
) on the boundary (
$\unicode[STIX]{x1D701}_{r}>0$
) on the boundary (
![]() $|\boldsymbol{x}|=1$
). Thus, we can conclude that
$|\boldsymbol{x}|=1$
). Thus, we can conclude that
![]() $\unicode[STIX]{x1D719}=0$
in the whole gas region. Then, equation (A 1b
) (with
$\unicode[STIX]{x1D719}=0$
in the whole gas region. Then, equation (A 1b
) (with
![]() $\unicode[STIX]{x1D6FA}=0$
) reduces to
$\unicode[STIX]{x1D6FA}=0$
) reduces to
Finally, due to the uniqueness condition for
![]() $K_{B0}$
,
$K_{B0}$
,
![]() $\unicode[STIX]{x1D70F}_{s}$
must vanish on the boundary. Thus, we conclude that
$\unicode[STIX]{x1D70F}_{s}$
must vanish on the boundary. Thus, we conclude that
![]() $\unicode[STIX]{x1D70F}_{s}=0$
also inside the sphere, since
$\unicode[STIX]{x1D70F}_{s}=0$
also inside the sphere, since
![]() $\unicode[STIX]{x1D70F}_{s}$
is constant.
$\unicode[STIX]{x1D70F}_{s}$
is constant.
One might think that the uniform temperature of the sphere and the gas (i.e.
![]() $\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{s}=0$
) is physically obvious for the following reason. In a slow flow for which a linearisation is applicable, the energy equation of the gas reduces to
$\unicode[STIX]{x1D70F}=\unicode[STIX]{x1D70F}_{s}=0$
) is physically obvious for the following reason. In a slow flow for which a linearisation is applicable, the energy equation of the gas reduces to
![]() $\unicode[STIX]{x2202}Q_{i}/\unicode[STIX]{x2202}x_{i}=0$
, which is identical to the energy equation in a solid body. Consequently, in the absence of heat sources in the body and under the condition of energy continuity across the surface, the radial heat flux through the sphere and the gas is zero, which results in a uniform temperature of the sphere and the gas. However, this argument does not hold in rarefied gases, though the result is still true for the present rotating flow. The reasons are the following. First, we cannot conclude that
$\unicode[STIX]{x2202}Q_{i}/\unicode[STIX]{x2202}x_{i}=0$
, which is identical to the energy equation in a solid body. Consequently, in the absence of heat sources in the body and under the condition of energy continuity across the surface, the radial heat flux through the sphere and the gas is zero, which results in a uniform temperature of the sphere and the gas. However, this argument does not hold in rarefied gases, though the result is still true for the present rotating flow. The reasons are the following. First, we cannot conclude that
![]() $\unicode[STIX]{x1D70F}=\text{const.}$
from
$\unicode[STIX]{x1D70F}=\text{const.}$
from
![]() $Q_{i}=0$
, since the Fourier law does not hold generally in rarefied gases. In the present problem,
$Q_{i}=0$
, since the Fourier law does not hold generally in rarefied gases. In the present problem,
![]() $\unicode[STIX]{x1D70F}\equiv 0$
is derived as a consequence of the similarity solution. Second, we cannot conclude that there is no radial heat flux in the sphere in the absence of heat sources inside when the ambient gas is a rarefied gas. In rarefied gases, the flow velocity and the heat flux are linked through the VDF, and if any non-zero radial heat flux is induced in the gas, it may cause a redistribution of the temperature (in a thermally neutral body), resulting in a non-uniform temperature distribution (thermal polarisation). The present linearised steady rotating flow is free from this effect because it produces no radial heat flux in the gas (i.e.
$\unicode[STIX]{x1D70F}\equiv 0$
is derived as a consequence of the similarity solution. Second, we cannot conclude that there is no radial heat flux in the sphere in the absence of heat sources inside when the ambient gas is a rarefied gas. In rarefied gases, the flow velocity and the heat flux are linked through the VDF, and if any non-zero radial heat flux is induced in the gas, it may cause a redistribution of the temperature (in a thermally neutral body), resulting in a non-uniform temperature distribution (thermal polarisation). The present linearised steady rotating flow is free from this effect because it produces no radial heat flux in the gas (i.e.
![]() $Q_{r}\equiv 0$
). Here, we stress again that the vanishing radial heat flux is a consequence of the similarity solution and is not derived from
$Q_{r}\equiv 0$
). Here, we stress again that the vanishing radial heat flux is a consequence of the similarity solution and is not derived from
![]() $\unicode[STIX]{x1D70F}\equiv 0$
. In rarefied gases,
$\unicode[STIX]{x1D70F}\equiv 0$
. In rarefied gases,
![]() $\unicode[STIX]{x1D70F}=\text{const.}$
and
$\unicode[STIX]{x1D70F}=\text{const.}$
and
![]() $Q_{i}=0$
are not equivalent. Indeed,
$Q_{i}=0$
are not equivalent. Indeed,
![]() $Q_{\unicode[STIX]{x1D711}}\neq 0$
despite
$Q_{\unicode[STIX]{x1D711}}\neq 0$
despite
![]() $\unicode[STIX]{x1D70F}\equiv 0$
in the present rotating flow. Incidentally, the thermal polarisation of a sphere has been extensively studied in the literature (see e.g. Beresnev, Chernyak & Fomyagin Reference Beresnev, Chernyak and Fomyagin1990; Takata & Sone Reference Takata and Sone1995, and references therein).
$\unicode[STIX]{x1D70F}\equiv 0$
in the present rotating flow. Incidentally, the thermal polarisation of a sphere has been extensively studied in the literature (see e.g. Beresnev, Chernyak & Fomyagin Reference Beresnev, Chernyak and Fomyagin1990; Takata & Sone Reference Takata and Sone1995, and references therein).
A steady non-uniform temperature distribution of the sphere and the surrounding gas without total heat production in a thermally adiabatic system does not conflict with the thermodynamic laws, when there are inputs of energy (i.e. work) per unit time. If this work is solely associated with the sphere rotation, the problem separation and the uniqueness result exclude such a possibility in the linearised framework.
Appendix B. Estimate of the first term on the right-hand side of (6.2)
In this appendix, we estimate the behaviour of the first term on the right-hand side of (6.2). To this end, we follow the basic strategy in Takata & Taguchi (Reference Takata and Taguchi2017) and summarise the main points.
Let us first consider the so-called partial model, obtained by omitting the gain term of the linearised ES equation (or the linearised Boltzmann equation):
which is supplemented by the boundary conditions (2.6) and (2.7). Here,
![]() $\unicode[STIX]{x1D708}_{c}=\unicode[STIX]{x1D708}_{c}(\unicode[STIX]{x1D701})>\unicode[STIX]{x1D6FF}({>}0)$
with
$\unicode[STIX]{x1D708}_{c}=\unicode[STIX]{x1D708}_{c}(\unicode[STIX]{x1D701})>\unicode[STIX]{x1D6FF}({>}0)$
with
![]() $\unicode[STIX]{x1D6FF}$
being a positive constant (
$\unicode[STIX]{x1D6FF}$
being a positive constant (
![]() $\unicode[STIX]{x1D708}_{c}=1$
in the case of the linearised ES model). After applying the form
$\unicode[STIX]{x1D708}_{c}=1$
in the case of the linearised ES model). After applying the form
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D719}_{S}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})\sin \unicode[STIX]{x1D703}$
, the solution
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D719}_{S}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})\sin \unicode[STIX]{x1D703}$
, the solution
![]() $\unicode[STIX]{x1D719}_{S}$
for the partial model is given by
$\unicode[STIX]{x1D719}_{S}$
for the partial model is given by
 $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{S}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})=\left\{\begin{array}{@{}ll@{}}2\unicode[STIX]{x1D6FC}r\exp \left(-{\displaystyle \frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}}\right),\quad & [0\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \text{Arcsin}(r^{-1})],\\ 0,\quad & [\text{Arcsin}(r^{-1})<\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}],\end{array}\right. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D719}_{S}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})=\left\{\begin{array}{@{}ll@{}}2\unicode[STIX]{x1D6FC}r\exp \left(-{\displaystyle \frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}}\right),\quad & [0\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \text{Arcsin}(r^{-1})],\\ 0,\quad & [\text{Arcsin}(r^{-1})<\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}],\end{array}\right. & \displaystyle\end{eqnarray}$$
Thus, in the case of the partial model, it is sufficient to consider the case of
![]() $\unicode[STIX]{x1D6FC}=1$
. Keeping this in mind, we evaluate the first term of (6.2) as follows:
$\unicode[STIX]{x1D6FC}=1$
. Keeping this in mind, we evaluate the first term of (6.2) as follows:
 $$\begin{eqnarray}\displaystyle \text{(first term)} & = & \displaystyle \unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}}{\unicode[STIX]{x2202}r}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left[r\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)\right]E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\left(1-\frac{\unicode[STIX]{x1D708}_{c}r}{k\unicode[STIX]{x1D701}}\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{\unicode[STIX]{x1D708}_{c}r^{2}\unicode[STIX]{x1D701}^{3}\sin ^{5}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{(first term)} & = & \displaystyle \unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}}{\unicode[STIX]{x2202}r}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}r}\left[r\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)\right]E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\left(1-\frac{\unicode[STIX]{x1D708}_{c}r}{k\unicode[STIX]{x1D701}}\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{\unicode[STIX]{x1D708}_{c}r^{2}\unicode[STIX]{x1D701}^{3}\sin ^{5}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}.\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
The first term obviously remains finite as
![]() $r\downarrow 1$
. On the other hand, the second term is estimated as
$r\downarrow 1$
. On the other hand, the second term is estimated as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left|\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{\unicode[STIX]{x1D708}_{c}r^{2}\unicode[STIX]{x1D701}^{3}\sin ^{5}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{\unicode[STIX]{x1D708}_{c}r^{2}\unicode[STIX]{x1D701}^{3}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{r^{2}}{(r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/2}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}=\left(\int _{0}^{\infty }\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\right)rK\left(\frac{1}{r}\right),\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left|\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{\unicode[STIX]{x1D708}_{c}r^{2}\unicode[STIX]{x1D701}^{3}\sin ^{5}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\right|\nonumber\\ \displaystyle & & \displaystyle \quad \leqslant \int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{\unicode[STIX]{x1D708}_{c}r^{2}\unicode[STIX]{x1D701}^{3}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle \quad =\int _{0}^{\infty }\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{r^{2}}{(r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/2}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}=\left(\int _{0}^{\infty }\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\right)rK\left(\frac{1}{r}\right),\qquad\end{eqnarray}$$
where
![]() $K(x)$
is the complete elliptic integral of the first kind. Since
$K(x)$
is the complete elliptic integral of the first kind. Since
![]() $K(x)\sim (1/2)\ln (16/(1-x^{2}))$
as
$K(x)\sim (1/2)\ln (16/(1-x^{2}))$
as
![]() $x\uparrow 1$
, we find that
$x\uparrow 1$
, we find that
as
![]() $r\downarrow 1$
. Thus, the second term diverges at most logarithmically. Also, notice that this logarithmic divergence of the first term of (6.2) does not occur when the gas is collisionless (
$r\downarrow 1$
. Thus, the second term diverges at most logarithmically. Also, notice that this logarithmic divergence of the first term of (6.2) does not occur when the gas is collisionless (
![]() $k=\infty$
), because the second term of (B 4) degenerates in this case.
$k=\infty$
), because the second term of (B 4) degenerates in this case.
Now we consider the following quasi-full model:
supplemented by the same boundary conditions as before, i.e. (2.6) and (2.7). Here,
![]() $S\equiv \unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}S_{1}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})$
represents a source term which is supposed to behave in the same way as the moments of
$S\equiv \unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\sin \unicode[STIX]{x1D703}S_{1}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})$
represents a source term which is supposed to behave in the same way as the moments of
![]() $\unicode[STIX]{x1D719}$
of the partial model as
$\unicode[STIX]{x1D719}$
of the partial model as
![]() $r\downarrow 1$
. The ES model obviously satisfies this property. That is,
$r\downarrow 1$
. The ES model obviously satisfies this property. That is,
![]() $S_{1}\sim a(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})+b(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})s^{1/2}+c(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})s\ln s+\cdots$
with
$S_{1}\sim a(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})+b(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})s^{1/2}+c(\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})s\ln s+\cdots$
with
![]() $s=r-1$
. The second term proportional to
$s=r-1$
. The second term proportional to
![]() $s^{1/2}$
is due to the contribution of the second term of (6.2).
$s^{1/2}$
is due to the contribution of the second term of (6.2).
Integrating the equation along the characteristics, the solution
![]() $\unicode[STIX]{x1D719}_{S}$
of
$\unicode[STIX]{x1D719}_{S}$
of
![]() $\unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D719}_{S}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})\sin \unicode[STIX]{x1D703}$
for the quasi-full model is given, for
$\unicode[STIX]{x1D719}=\unicode[STIX]{x1D6FA}\unicode[STIX]{x1D701}_{\unicode[STIX]{x1D711}}\unicode[STIX]{x1D719}_{S}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})\sin \unicode[STIX]{x1D703}$
for the quasi-full model is given, for
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in [0,\text{Arcsin}(r^{-1}))$
, as follows:
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in [0,\text{Arcsin}(r^{-1}))$
, as follows:
Here,
![]() $\unicode[STIX]{x1D70E}_{B}=\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})$
is given by (B 3) and
$\unicode[STIX]{x1D70E}_{B}=\unicode[STIX]{x1D70E}_{B}(r,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})$
is given by (B 3) and
In order to verify that the inclusion of the source term does not change the behaviour of the moment of the partial model, we go back to the first term of (6.2) and consider the following partial integral:
Substituting
![]() $\unicode[STIX]{x1D719}_{S}$
into this expression, we obtain, after some manipulations,
$\unicode[STIX]{x1D719}_{S}$
into this expression, we obtain, after some manipulations,
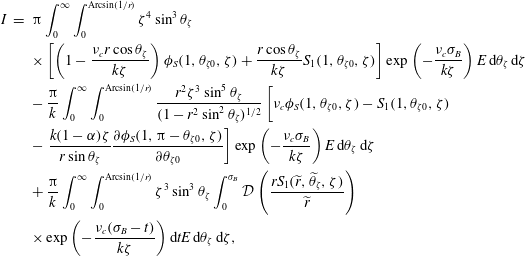 $$\begin{eqnarray}\displaystyle I & = & \displaystyle \unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \times \left[\left(1-\frac{\unicode[STIX]{x1D708}_{c}r\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{k\unicode[STIX]{x1D701}}\right)\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})+\frac{r\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{k\unicode[STIX]{x1D701}}S_{1}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})\right]\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{r^{2}\unicode[STIX]{x1D701}^{3}\sin ^{5}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}\left[\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})-S_{1}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})\vphantom{\frac{(1-\unicode[STIX]{x1D701})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{k(1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D701}}{r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}\right]\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{3}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\int _{0}^{\unicode[STIX]{x1D70E}_{B}}{\mathcal{D}}\left(\frac{rS_{1}(\widetilde{r},\widetilde{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})}{\widetilde{r}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(-\frac{\unicode[STIX]{x1D708}_{c}(\unicode[STIX]{x1D70E}_{B}-t)}{k\unicode[STIX]{x1D701}}\right)\text{d}tE\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle I & = & \displaystyle \unicode[STIX]{x03C0}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{4}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\nonumber\\ \displaystyle & & \displaystyle \times \left[\left(1-\frac{\unicode[STIX]{x1D708}_{c}r\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{k\unicode[STIX]{x1D701}}\right)\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})+\frac{r\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{k\unicode[STIX]{x1D701}}S_{1}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})\right]\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\frac{r^{2}\unicode[STIX]{x1D701}^{3}\sin ^{5}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{(1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})^{1/2}}\left[\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})-S_{1}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})\vphantom{\frac{(1-\unicode[STIX]{x1D701})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\right.\nonumber\\ \displaystyle & & \displaystyle -\left.\frac{k(1-\unicode[STIX]{x1D6FC})\unicode[STIX]{x1D701}}{r\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x03C0}-\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0},\unicode[STIX]{x1D701})}{\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}\right]\exp \left(-\frac{\unicode[STIX]{x1D708}_{c}\unicode[STIX]{x1D70E}_{B}}{k\unicode[STIX]{x1D701}}\right)E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{3}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\int _{0}^{\unicode[STIX]{x1D70E}_{B}}{\mathcal{D}}\left(\frac{rS_{1}(\widetilde{r},\widetilde{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})}{\widetilde{r}}\right)\nonumber\\ \displaystyle & & \displaystyle \times \exp \left(-\frac{\unicode[STIX]{x1D708}_{c}(\unicode[STIX]{x1D70E}_{B}-t)}{k\unicode[STIX]{x1D701}}\right)\text{d}tE\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701},\end{eqnarray}$$
where
Note that (B 4) for the partial model is recovered by setting
![]() $\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})=2$
(
$\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})=2$
(
![]() $0\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}/2$
) and
$0\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}/2$
) and
![]() $S_{1}=0$
as well as
$S_{1}=0$
as well as
![]() $\unicode[STIX]{x1D6FC}=1$
. Clearly, the first term remains finite as
$\unicode[STIX]{x1D6FC}=1$
. Clearly, the first term remains finite as
![]() $r\downarrow 1$
if
$r\downarrow 1$
if
![]() $|\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})|$
is bounded for the impinging molecules,
$|\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})|$
is bounded for the impinging molecules,
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. The second term involves the derivative of
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. The second term involves the derivative of
![]() $\unicode[STIX]{x1D719}_{S}$
with respect to
$\unicode[STIX]{x1D719}_{S}$
with respect to
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}$
on the boundary for the impinging molecules,
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}$
on the boundary for the impinging molecules,
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. We will see later that this remains finite. Therefore, essentially the same estimate as in the case of the partial model applies and the integral is estimated to be logarithmically diverging as
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. We will see later that this remains finite. Therefore, essentially the same estimate as in the case of the partial model applies and the integral is estimated to be logarithmically diverging as
![]() $r\downarrow 1$
. For the third term, we first note that
$r\downarrow 1$
. For the third term, we first note that
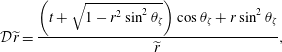 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}\widetilde{r}=\frac{\left(t+\sqrt{1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}\right)\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}+r\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{\widetilde{r}}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}\widetilde{r}=\frac{\left(t+\sqrt{1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}\right)\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}+r\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}{\widetilde{r}}, & \displaystyle\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}\widetilde{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D701}}=\frac{\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\left(t+\sqrt{1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}-r\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\right)}{\widetilde{r}^{2}}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle {\mathcal{D}}\widetilde{\unicode[STIX]{x1D703}}_{\unicode[STIX]{x1D701}}=\frac{\sin \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\left(t+\sqrt{1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}}-r\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\right)}{\widetilde{r}^{2}}. & \displaystyle\end{eqnarray}$$
Then, since
![]() $|\unicode[STIX]{x2202}S_{1}/\unicode[STIX]{x2202}r|\sim C/\sqrt{r-1}$
for some positive constant
$|\unicode[STIX]{x2202}S_{1}/\unicode[STIX]{x2202}r|\sim C/\sqrt{r-1}$
for some positive constant
![]() $C$
as
$C$
as
![]() $r\downarrow 1$
, we have the following estimate (since
$r\downarrow 1$
, we have the following estimate (since
![]() $t\leqslant \unicode[STIX]{x1D70E}_{B}$
in the range of integration,
$t\leqslant \unicode[STIX]{x1D70E}_{B}$
in the range of integration,
![]() ${\mathcal{D}}\widetilde{r}\leqslant ((\unicode[STIX]{x1D70E}_{B}+\sqrt{1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}})\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}+r\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})/\widetilde{r}=(r\cos ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}+r\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})/\widetilde{r}=r/\widetilde{r}$
):
${\mathcal{D}}\widetilde{r}\leqslant ((\unicode[STIX]{x1D70E}_{B}+\sqrt{1-r^{2}\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}})\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}+r\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})/\widetilde{r}=(r\cos ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}+r\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}})/\widetilde{r}=r/\widetilde{r}$
):
Thus, we are left to examine the integral
Since
 $$\begin{eqnarray}\displaystyle \frac{1}{\sqrt{\widetilde{r}-1}} & = & \displaystyle \frac{\sqrt{\widetilde{r}+1}}{\sqrt{\widetilde{r}^{2}-1}}=\frac{\sqrt{\widetilde{r}+1}}{\sqrt{t^{2}+2t\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\leqslant \frac{\sqrt{r+1}}{t^{1/2}\sqrt{t+2\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{\sqrt{r+1}}{t^{1/2}\sqrt{2\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\leqslant \frac{\sqrt{2}r}{t^{1/2}\sqrt{2\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}=\frac{r}{t^{1/2}\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{1}{\sqrt{\widetilde{r}-1}} & = & \displaystyle \frac{\sqrt{\widetilde{r}+1}}{\sqrt{\widetilde{r}^{2}-1}}=\frac{\sqrt{\widetilde{r}+1}}{\sqrt{t^{2}+2t\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\leqslant \frac{\sqrt{r+1}}{t^{1/2}\sqrt{t+2\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{\sqrt{r+1}}{t^{1/2}\sqrt{2\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\leqslant \frac{\sqrt{2}r}{t^{1/2}\sqrt{2\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}=\frac{r}{t^{1/2}\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}},\end{eqnarray}$$
we have
 $$\begin{eqnarray}\displaystyle J & {\leqslant} & \displaystyle \frac{\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{3}r^{3}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{1}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\int _{0}^{\unicode[STIX]{x1D70E}_{B}}\frac{\text{d}t}{t^{1/2}}E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{3}r^{3}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{\sqrt{\unicode[STIX]{x1D70E}_{B}}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\frac{\sqrt{\unicode[STIX]{x1D70E}_{B}}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{\sqrt{r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J & {\leqslant} & \displaystyle \frac{\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{3}r^{3}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{1}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\int _{0}^{\unicode[STIX]{x1D70E}_{B}}\frac{\text{d}t}{t^{1/2}}E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\int _{0}^{\text{Arcsin}(1/r)}\unicode[STIX]{x1D701}^{3}r^{3}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\frac{\sqrt{\unicode[STIX]{x1D70E}_{B}}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}E\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\,\text{d}\unicode[STIX]{x1D701}\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\frac{\sqrt{\unicode[STIX]{x1D70E}_{B}}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{\sqrt{r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}.\end{eqnarray}$$
But, since
 $$\begin{eqnarray}\displaystyle J & {\leqslant} & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\frac{(r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/4}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{\sqrt{r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{(r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/4}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{1}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{(1-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/4}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}=\frac{\unicode[STIX]{x03C0}^{2}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle J & {\leqslant} & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\frac{(r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/4}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{\sqrt{r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{\sin ^{3}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{(r^{2}-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/4}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\frac{1}{\sqrt{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}}\frac{\cos \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}}{(1-\sin ^{2}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0})^{1/4}}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}\nonumber\\ \displaystyle & = & \displaystyle \frac{2\unicode[STIX]{x03C0}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}\int _{0}^{\unicode[STIX]{x03C0}/2}\,\text{d}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}0}=\frac{\unicode[STIX]{x03C0}^{2}}{k}\int _{0}^{\infty }\unicode[STIX]{x1D701}^{3}E\,\text{d}\unicode[STIX]{x1D701}.\end{eqnarray}$$
Thus, the third term is also bounded.
We close this appendix by showing the boundedness of
![]() $|\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}|$
at
$|\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}|$
at
![]() $r=1$
for
$r=1$
for
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. This is directly seen by writing
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. This is directly seen by writing
![]() $\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})$
for
$\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})$
for
![]() $\unicode[STIX]{x03C0}/2\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}$
as (see (B 8))
$\unicode[STIX]{x03C0}/2\leqslant \unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\leqslant \unicode[STIX]{x03C0}$
as (see (B 8))
where
Thus, recalling again that
![]() $|\unicode[STIX]{x2202}S_{1}/\unicode[STIX]{x2202}r|\sim C/\sqrt{r-1}$
as
$|\unicode[STIX]{x2202}S_{1}/\unicode[STIX]{x2202}r|\sim C/\sqrt{r-1}$
as
![]() $r\downarrow 1$
, we have the estimate
$r\downarrow 1$
, we have the estimate
uniformly in
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. In view of this, we consider the integral
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
. In view of this, we consider the integral
Since
Thus,
![]() $|\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}|$
is bounded for
$|\unicode[STIX]{x2202}\unicode[STIX]{x1D719}_{S}(1,\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D701})/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}|$
is bounded for
![]() $\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
.
$\unicode[STIX]{x1D703}_{\unicode[STIX]{x1D701}}\in (\unicode[STIX]{x03C0}/2,\unicode[STIX]{x03C0}]$
.