Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-10T07:36:14.643Z Has data issue: false hasContentIssue false
  • English
  • Français

Rayleigh–Bénard convection in a creeping solid with melting and freezing at either or both its horizontal boundaries

Published online by Cambridge University Press:  03 May 2018

Stéphane Labrosse Open the ORCID record for Stéphane Labrosse [Opens in a new window] ,
Adrien Morison ,
Renaud Deguen  and
Thierry Alboussière Open the ORCID record for Thierry Alboussière [Opens in a new window]
Stéphane Labrosse*
Affiliation:
Université de Lyon, ENSL, UCBL, CNRS, LGL-TPE, 46 allée d’Italie, F-69364 Lyon, France
Adrien Morison
Affiliation:
Université de Lyon, ENSL, UCBL, CNRS, LGL-TPE, 46 allée d’Italie, F-69364 Lyon, France
Renaud Deguen
Affiliation:
Université de Lyon, ENSL, UCBL, CNRS, LGL-TPE, 46 allée d’Italie, F-69364 Lyon, France
Thierry Alboussière
Affiliation:
Université de Lyon, ENSL, UCBL, CNRS, LGL-TPE, 46 allée d’Italie, F-69364 Lyon, France
*
†Email address for correspondence: stephane.labrosse@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Solid-state convection can take place in the rocky or icy mantles of planetary objects, and these mantles can be surrounded above or below or both by molten layers of similar composition. A flow towards the interface can proceed through it by changing phase. This behaviour is modelled by a boundary condition taking into account the competition between viscous stress in the solid, which builds topography of the interface with a time scale 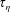$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$ , and convective transfer of the latent heat in the liquid from places of the boundary where freezing occurs to places of melting, which acts to erase topography, with a time scale 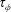$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D719}}$ . The ratio 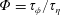$\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D719}}/\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D702}}$ controls whether the boundary condition is the classical non-penetrative one ( 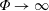$\unicode[STIX]{x1D6F7}\rightarrow \infty$ ) or allows for a finite flow through the boundary (small 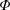$\unicode[STIX]{x1D6F7}$ ). We study Rayleigh–Bénard convection in a plane layer subject to this boundary condition at either or both its boundaries using linear and weakly nonlinear analyses. When both boundaries are phase-change interfaces with equal values of 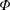$\unicode[STIX]{x1D6F7}$ , a non-deforming translation mode is possible with a critical Rayleigh number equal to 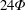$24\unicode[STIX]{x1D6F7}$ . At small values of 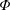$\unicode[STIX]{x1D6F7}$ , this mode competes with a weakly deforming mode having a slightly lower critical Rayleigh number and a very long wavelength, 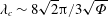$\unicode[STIX]{x1D706}_{c}\sim 8\sqrt{2}\unicode[STIX]{x03C0}/3\sqrt{\unicode[STIX]{x1D6F7}}$ . Both modes lead to very efficient heat transfer, as expressed by the relationship between the Nusselt and Rayleigh numbers. When only one boundary is subject to a phase-change condition, the critical Rayleigh number is 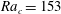$\mathit{Ra}_{c}=153$ and the critical wavelength is 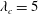$\unicode[STIX]{x1D706}_{c}=5$ . The Nusselt number increases approximately two times faster with the Rayleigh number than in the classical case with non-penetrative conditions, and the average temperature diverges from 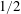$1/2$ when the Rayleigh number is increased, towards larger values when the bottom boundary is a phase-change interface.

JFM classification

Convection: Buoyancy-driven instability Geophysical and Geological Flows: Mantle convection Phase change: Solidification/melting
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 846 , 10 July 2018 , pp. 5 - 36
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alboussière, T., Deguen, R. & Melzani, M. 2010 Melting-induced stratification above the Earth’s inner core due to convective translation. Nature 466, 744–747.CrossRefGoogle ScholarPubMed
Baland, R.-M., Tobie, G., Lefèvre, A. & van Hoolst, T. 2014 Titan’s internal structure inferred from its gravity field, shape, and rotation state. Icarus 237 (0), 29–41.Google Scholar
Bercovici, D. & Ricard, Y. 2014 Plate tectonics, damage and inheritance. Nature 508, 513–516.Google Scholar
Čadek, O., Tobie, G., Van Hoolst, T., Massé, M., Choblet, G., Lefèvre, A., Mitri, G., Baland, R.-M., Běhounková, M., Bourgeois, O. & Trinh, A. 2016 Enceladus’s internal ocean and ice shell constrained from Cassini gravity, shape, and libration data. Geophys. Res. Lett. 43 (11), 5653–5660; 2016GL068634.Google Scholar
Canuto, C., Hussaini, M., Quarteroni, A. & Zang, T. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Christensen, U. R. & Yuen, D. A. 1989 Time-dependent convection with non-Newtonian viscosity. J. Geophys. Res. 94 (B1), 814–820.Google Scholar
Crank, J. 1984 Free and Moving Boundary Problems, 425 pp. Oxford University Press.Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside of equilibrium. Rev. Mod. Phys. 65 (3), 851–1112.Google Scholar
Davaille, A. & Jaupart, C. 1993 Transient high-Rayleigh-number thermal convection with large viscosity variations. J. Fluid Mech. 253, 141–166.Google Scholar
Deguen, R. 2013 Thermal convection in a spherical shell with melting/freezing at either or both of its boundaries. J. Earth Sci. 24, 669–682.Google Scholar
Deguen, R., Alboussière, T. & Cardin, P. 2013 Thermal convection in Earth’s inner core with phase change at its boundary. Geophys. J. Intl 194, 1310–1334.Google Scholar
Elkins-Tanton, L. T. 2012 Magma oceans in the inner solar system. Annu. Rev. Earth Planet. Sci. 40, 113–139.Google Scholar
Gaidos, E. J. & Nimmo, F. 2000 Planetary science: tectonics and water on Europa. Nature 405 (6787), 637.Google Scholar
Grasset, O., Sotin, C. & Deschamps, F. 2000 On the internal structure and dynamics of Titan. Planet. Space Sci. 48 (7–8), 617–636.Google Scholar
Guo, W., Labrosse, G. & Narayanan, R. 2012 The Application of the Chebyshev-Spectral Method in Transport Phenomena. Springer-Verlag.Google Scholar
Jarvis, G. T. & McKenzie, D. P. 1980 Convection in a compressible fluid with infinite Prandtl number. J. Fluid Mech. 96, 515–583.Google Scholar
Jeffreys, H. 1930 The instability of a compressible fluid heated below. Math. Proc. Camb. Phil. Soc. 26, 170–172.Google Scholar
Khurana, K. K., Kivelson, M. G., Stevenson, D. J., Schubert, G., Russell, C. T., Walker, R. J. & Polanskey, C. 1998 Induced magnetic fields as evidence for subsurface oceans in Europa and Callisto. Nature 395 (6704), 777–780.Google Scholar
Labrosse, S., Hernlund, J. W. & Coltice, N. 2007 A crystallizing dense magma ocean at the base of Earth’s mantle. Nature 450, 866–869.Google Scholar
Malkus, W. V. R. & Veronis, G. 1958 Finite amplitude cellular convection. J. Fluid Mech. 4, 225–260.CrossRefGoogle Scholar
Manneville, P. 2004 Instabilities, Chaos and Turbulence – An Introduction to Nonlinear Dynamics and Complex Systems. Imperial College Press.Google Scholar
McKenzie, D. P., Roberts, J. M. & Weiss, N. O. 1974 Convection in the Earth’s mantle: towards a numerical simulation. J. Fluid Mech. 62, 465–538.CrossRefGoogle Scholar
Mizzon, H. & Monnereau, M. 2013 Implication of the lopsided growth for the viscosity of Earth’s inner core. Earth Planet. Sci. Lett. 361, 391–401.Google Scholar
Monnereau, M., Calvet, M., Margerin, L. & Souriau, A. 2010 Lopsided growth of Earth’s inner core. Science 328 (5981), 1014–1017.Google Scholar
Monnereau, M. & Dubuffet, F. 2002 Is Io’s mantle really molten? Icarus 158, 450–459.Google Scholar
Pappalardo, R. T., Head, J. W., Greeley, R., Sullivan, R. J., Pilcher, C., Schubert, G., Moore, W. B., Carr, M. H., Moore, J. M., Belton, M. J. S. & Goldsby, D. L. 1998 Geological evidence for solid-state convection in Europa’s ice shell. Nature 391 (6665), 365–368.Google Scholar
Parmentier, E. M. 1978 Study of thermal-convection in non-Newtonian fluids. J. Fluid Mech. 84, 1–11.Google Scholar
Parmentier, E. M. & Sotin, C. 2000 Three-dimensional numerical experiments on thermal convection in a very viscous fluid: implications for the dynamics of a thermal boundary layer at high Rayleigh number. Phys. Fluids 12 (3), 609–617.Google Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics, 2nd edn. Springer.Google Scholar
Rayleigh, Lord 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32, 529–546.Google Scholar
Ricard, Y., Labrosse, S. & Dubuffet, F. 2014 Lifting the cover of the cauldron: convection in hot planets. Geochem. Geophys. Geosyst. 15, 4617–4630.Google Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76 (9), 6801.CrossRefGoogle ScholarPubMed
Schlüter, A., Lortz, D. & Busse, F. 1965 On the stability of steady finite amplitude convection. J. Fluid Mech. 23, 129–144.Google Scholar
Schubert, G., Turcotte, D. L. & Olson, P. 2001 Mantle Convection in the Earth and Planets. Cambridge University Press.Google Scholar
Soderlund, K. M., Schmidt, B. E., Wicht, J. & Blankenship, D. D. 2014 Ocean-driven heating of Europa’s icy shell at low latitudes. Nat. Geosci. 7 (1), 16–19.Google Scholar
Sohl, F., Hussmann, H., Schwentker, B., Spohn, T. & Lorenz, R. D. 2003 Interior structure models and tidal Love numbers of Titan. J. Geophys. Res. 108 (E12), 5130.Google Scholar
Solomatov, V. S. 2007 Magma oceans and primordial mantle differentiation. Treatise Geophys. 9, 91–120.CrossRefGoogle Scholar
Tackley, P. J. 2000 Self-consistent generation of tectonic plates in time-dependent, three-dimensional mantle convection simulations 1. Pseudoplastic yielding. Geochem. Geophys. Geosyst. 1, 2000Gc000041.Google Scholar
Tobie, G., Choblet, G. & Sotin, C. 2003 Tidally heated convection: constraints on Europa’s ice shell thickness. J. Geophys. Res. 108, 5124.Google Scholar
Turcotte, D. L. & Oxburgh, E. R. 1967 Finite amplitude convective cells and continental drift. J. Fluid Mech. 28, 29–42.Google Scholar
Turcotte, D. L. & Schubert, G. 2001 Geodynamics, 2nd edn. Cambridge University Press.Google Scholar
Weideman, J. A. & Reddy, S. C. 2000 A Matlab differentiation matrix suite. ACM Trans. Math. Softw. 26 (4), 465–519.Google Scholar