Article contents
Rayleigh–Bénard convection with an immersed floating body
Published online by Cambridge University Press: 11 January 2024
Abstract
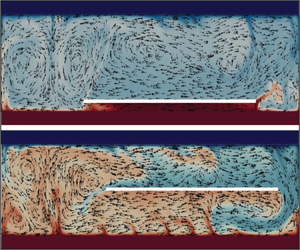
The paper presents the results of an experimental and numerical study of turbulent thermal convection in a rectangular box containing an extended immersed free-floating plate. Varying the values of control parameters, such as Rayleigh number, aspect ratio and vertical position of the plate, provides a wide range of possible modes, from immobile and purely periodic to stochastic. We have shown that stable periodic motions occur when the plate floats close to one of the heat exchangers. An increase in the distance between the plate and the heat exchanger breaks the periodic motion and (at moderate Rayleigh numbers) leads to a pronounced asymmetry, when the plate stays close to one of the walls most of the time, makes rare excursions to the opposite wall and immediately returns. As the Rayleigh number increases, the plate motions from one edge of the box to the other reappear, but always have an irregular character. Regarding the dependence of the system behaviour on the geometry of the box, both lower and upper limits of periodic plate motions were found in the experiments. In the numerical simulations, the upper limit was not achieved – the plate moves quasi-periodically through the chain of vortices of different signs even at the largest aspect ratio being considered. The heat-insulating floating plate provides the spatial and temporal variation of the heat flux and reduces the integral heat flux, but the reduction in heat flux depends significantly on the vertical position of the plate.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
- 6
- Cited by


