Article contents
Rayleigh–Bénard stability and the validity of quasi-Boussinesq or quasi-anelastic liquid approximations
Published online by Cambridge University Press: 16 March 2017
Abstract
The linear stability threshold of the Rayleigh–Bénard configuration is analysed with compressible effects taken into account. It is assumed that the fluid under investigation obeys a Newtonian rheology and Fourier’s law of thermal transport with constant, uniform (dynamic) viscosity and thermal conductivity in a uniform gravity field. Top and bottom boundaries are maintained at different constant temperatures and we consider here mechanical boundary conditions of zero tangential stress and impermeable walls. Under these conditions, and with the Boussinesq approximation, Rayleigh (Phil. Mag., vol. 32 (192), 1916, pp. 529–546) first obtained analytically the critical value 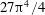 $27\unicode[STIX]{x03C0}^{4}/4$ for a dimensionless parameter, now known as the Rayleigh number, at the onset of convection. This paper describes the changes of the critical Rayleigh number due to the compressibility of the fluid, measured by the dimensionless dissipation parameter
$27\unicode[STIX]{x03C0}^{4}/4$ for a dimensionless parameter, now known as the Rayleigh number, at the onset of convection. This paper describes the changes of the critical Rayleigh number due to the compressibility of the fluid, measured by the dimensionless dissipation parameter 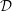 ${\mathcal{D}}$ and due to a finite temperature difference between the hot and cold boundaries, measured by a dimensionless temperature gradient
${\mathcal{D}}$ and due to a finite temperature difference between the hot and cold boundaries, measured by a dimensionless temperature gradient  $a$ . Different equations of state are examined: ideal gas equation, Murnaghan’s model (often used to describe the interiors of solid but convective planets) and a generic equation of state with adjustable parameters, which can represent any possible equation of state. In the perspective to assess approximations often made in convective models, we also consider two variations of this stability analysis. In a so-called quasi-Boussinesq model, we consider that density perturbations are solely due to temperature perturbations. In a so-called quasi-anelastic liquid approximation model, we consider that entropy perturbations are solely due to temperature perturbations. In addition to the numerical Chebyshev-based stability analysis, an analytical approximation is obtained when temperature fluctuations are written as a combination of only two modes, one being the original symmetrical (between top and bottom) mode introduced by Rayleigh, the other one being antisymmetrical. The analytical solution allows us to show that the antisymmetrical part of the critical eigenmode increases linearly with the parameters
$a$ . Different equations of state are examined: ideal gas equation, Murnaghan’s model (often used to describe the interiors of solid but convective planets) and a generic equation of state with adjustable parameters, which can represent any possible equation of state. In the perspective to assess approximations often made in convective models, we also consider two variations of this stability analysis. In a so-called quasi-Boussinesq model, we consider that density perturbations are solely due to temperature perturbations. In a so-called quasi-anelastic liquid approximation model, we consider that entropy perturbations are solely due to temperature perturbations. In addition to the numerical Chebyshev-based stability analysis, an analytical approximation is obtained when temperature fluctuations are written as a combination of only two modes, one being the original symmetrical (between top and bottom) mode introduced by Rayleigh, the other one being antisymmetrical. The analytical solution allows us to show that the antisymmetrical part of the critical eigenmode increases linearly with the parameters  $a$ and
$a$ and 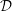 ${\mathcal{D}}$ , while the superadiabatic critical Rayleigh number departs quadratically in
${\mathcal{D}}$ , while the superadiabatic critical Rayleigh number departs quadratically in  $a$ and
$a$ and 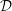 ${\mathcal{D}}$ from
${\mathcal{D}}$ from 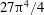 $27\unicode[STIX]{x03C0}^{4}/4$ . For any arbitrary equation of state, the coefficients of the quadratic departure are determined analytically from the coefficients of the expansion of density up to degree three in terms of pressure and temperature.
$27\unicode[STIX]{x03C0}^{4}/4$ . For any arbitrary equation of state, the coefficients of the quadratic departure are determined analytically from the coefficients of the expansion of density up to degree three in terms of pressure and temperature.
JFM classification
Information
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 11
- Cited by


