Article contents
Reaction induced interfacial instability of miscible fluids in a channel
Published online by Cambridge University Press: 19 August 2021
Abstract
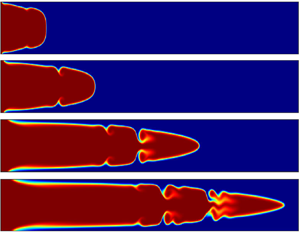
When a less viscous miscible fluid displaces a more-viscous one under a pressure-driven channel flow, unstable Kelvin–Helmholtz (K–H)-type billows are formed at the miscible interface. In this paper, we investigate whether such instability can be induced by a simple ( $\textbf {A}+ \textbf {B} \rightarrow \textbf {C}$)-type chemical reaction. Here a miscible solution of one reactant
$\textbf {A}+ \textbf {B} \rightarrow \textbf {C}$)-type chemical reaction. Here a miscible solution of one reactant  $\textbf {A}$ is displacing another isoviscous reactant
$\textbf {A}$ is displacing another isoviscous reactant  $\textbf {B}$ and producing a more-viscous product
$\textbf {B}$ and producing a more-viscous product  $\textbf {C}$ at the reactive front. It is found that because of a local increase in viscosity gradient due to the formation of more-viscous product
$\textbf {C}$ at the reactive front. It is found that because of a local increase in viscosity gradient due to the formation of more-viscous product  $\textbf {C}$, K–H-type billows are formed at the
$\textbf {C}$, K–H-type billows are formed at the  $\textbf {A}$–
$\textbf {A}$– $\textbf {C}$ interface. The changes in dynamical properties of such billows are examined by varying the governing parameters such as the mobility ratio
$\textbf {C}$ interface. The changes in dynamical properties of such billows are examined by varying the governing parameters such as the mobility ratio  $R_{c}$, Damköhler number
$R_{c}$, Damköhler number  $Da$, Péclet number
$Da$, Péclet number  $Pe$ and Reynolds number
$Pe$ and Reynolds number  $Re$. Interestingly, we have found that even at high reaction rates (sufficiently large
$Re$. Interestingly, we have found that even at high reaction rates (sufficiently large  $Da$) for
$Da$) for  $R_{c}=1$, the interface remains stable and for larger values of
$R_{c}=1$, the interface remains stable and for larger values of  $R_{c} (=3, 5)$ the K–H billows are observed. It is also noticed that a laminar horseshoe-type vortex develops near the wall at the channel inlet where the less-viscous reactant pushes the more-viscous product. We have computed numerically the onset time (
$R_{c} (=3, 5)$ the K–H billows are observed. It is also noticed that a laminar horseshoe-type vortex develops near the wall at the channel inlet where the less-viscous reactant pushes the more-viscous product. We have computed numerically the onset time ( $t_{on}$) of instability to understand the early-stage developments of the K–H billows. For different values of
$t_{on}$) of instability to understand the early-stage developments of the K–H billows. For different values of  $Da$, we have shown the unstable and stable time zones in the (
$Da$, we have shown the unstable and stable time zones in the ( $t_{on}$–
$t_{on}$– $R_{c}$) space. The bipartite (
$R_{c}$) space. The bipartite ( $t_{on}$–
$t_{on}$– $R_{c}$) space also depicts the critical (
$R_{c}$) space also depicts the critical ( $Da$-,
$Da$-,  $Pe$- and
$Pe$- and  $Re$-dependent)
$Re$-dependent)  $R_{c}$ value for which instability can be triggered in a finite desirable time. The delay in the onset of instability is observed with increasing
$R_{c}$ value for which instability can be triggered in a finite desirable time. The delay in the onset of instability is observed with increasing  $Pe$. Further it is shown that
$Pe$. Further it is shown that  $t_{on}$ can be linearly scaled with
$t_{on}$ can be linearly scaled with  $Pe$ to have a modified onset time (
$Pe$ to have a modified onset time ( $t^{*}_{on}$), which establishes a proportionate dynamics with respect to
$t^{*}_{on}$), which establishes a proportionate dynamics with respect to  $Pe$ in the early stages of the instability. Moreover, a reverse dependency of onset on lower
$Pe$ in the early stages of the instability. Moreover, a reverse dependency of onset on lower  $R_{c}$ values for higher Reynolds numbers is observed.
$R_{c}$ values for higher Reynolds numbers is observed.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 8
- Cited by


