Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T13:13:29.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduced-order representation of near-wall structures in the late transitional boundary layer

Published online by Cambridge University Press:  28 April 2014

Taraneh Sayadi ,
Peter J. Schmid ,
Joseph W. Nichols  and
Parviz Moin
Taraneh Sayadi*
Affiliation:
Laboratoire d’Hydrodynamique (LadHyX), Ecole Polytechnique, 91128 Palaiseau, France
Peter J. Schmid
Affiliation:
Department of Mathematics, Imperial College London, South Kensington Campus, London SW7 2AZ, UK
Joseph W. Nichols
Affiliation:
Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Parviz Moin
Affiliation:
Centre for Turbulence Research (CTR), Stanford University, Stanford, CA 94305, USA
*
†Email address for correspondence: tsayadi@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Direct numerical simulations (DNS) of controlled H- and K-type transitions to turbulence in an 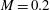$M = 0.2$ (where 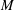$M$ is the Mach number) nominally zero-pressure-gradient and spatially developing flat-plate boundary layer are considered. Sayadi, Hamman & Moin (J. Fluid Mech., vol. 724, 2013, pp. 480–509) showed that with the start of the transition process, the skin-friction profiles of these controlled transitions diverge abruptly from the laminar value and overshoot the turbulent estimation. The objective of this work is to identify the structures of dynamical importance throughout the transitional region. Dynamic mode decomposition (DMD) (Schmid, J. Fluid Mech., vol. 656, 2010, pp. 5–28) as an optimal phase-averaging process, together with triple decomposition (Reynolds & Hussain, J. Fluid Mech., vol. 54 (02), 1972, pp. 263–288), is employed to assess the contribution of each coherent structure to the total Reynolds shear stress. This analysis shows that low-frequency modes, corresponding to the legs of hairpin vortices, contribute most to the total Reynolds shear stress. The use of composite DMD of the vortical structures together with the skin-friction coefficient allows the assessment of the coupling between near-wall structures captured by the low-frequency modes and their contribution to the total skin-friction coefficient. We are able to show that the low-frequency modes provide an accurate estimate of the skin-friction coefficient through the transition process. This is of interest since large-eddy simulation (LES) of the same configuration fails to provide a good prediction of the rise to this overshoot. The reduced-order representation of the flow is used to compare the LES and the DNS results within this region. Application of this methodology to the LES of the H-type transition illustrates the effect of the grid resolution and the subgrid-scale model on the estimated shear stress of these low-frequency modes. The analysis shows that although the shapes and frequencies of the low-frequency modes are independent of the resolution, the amplitudes are underpredicted in the LES, resulting in underprediction of the Reynolds shear stress.

JFM classification

Boundary Layers: Boundary layer structure Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 278 - 301
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aubry, N., Holmes, P., Lumley, J. L. & Stone, E. 1988 The dynamics of coherent structure in the wall region of a turbulent boundary layer. J. Fluid Mech. 192, 115–173.Google Scholar
Bake, S., Fernholz, H. H. & Kachanov, Y. S. 2000 Resemblance of K- and N-regimes of boundary-layer transition at late stages. Eur. J. Mech. (B/Fluids) 19 (1), 1–22.Google Scholar
Bakewell, H. P. Jr. & Lumley, J. L. 1967 Viscous sublayer and adjacent wall region in turbulent pipe flow. Phys. Fluids 10 (9), 1880–1889.Google Scholar
Berlin, S., Wiegel, M. & Henningson, D. S. 1999 Numerical and experimental investigations of oblique boundary layer transition. J. Fluid Mech. 393, 23–57.CrossRefGoogle Scholar
Borodulin, V. & Kachanov, Y. 1995 Formation and development of coherent structures in a transitional boundary layer. J. Appl. Mech. Tech. Phys. 36 (4), 532–564.Google Scholar
Borodulin, V. I., Kachanov, Y. S. & Roschektayev, A. P. 2011 Experimental detection of deterministic turbulence. J. Turbul. N23.Google Scholar
Chen, K. K., Tu, J. H. & Rowley, C. W. 2012 Variants of dynamic mode decomposition: boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 22 (6), 887–915.Google Scholar
Choi, H., Moin, P. & Kim, J. 1993 Direct numerical simulation of turbulent flow over riblets. J. Fluid Mech. 255, 503–539.Google Scholar
Head, M. R. & Bandyopadhyay, P. 1981 New aspects of turbulent boundary-layer structure. J. Fluid Mech. 107, 297–338.Google Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry, Cambridge Monographs on Mechanics. Cambridge University Press and McGraw-Hill.CrossRefGoogle Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, stream, and convergence zones in turbulent flows. Center for Turbulence Research Report. CTR-S88, pp. 193–208.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.Google Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
Kachanov, Y. S. & Levchenko, V. Y. 1984 The resonant interaction of disturbances at laminar–turbulent transition in a boundary layer. J. Fluid Mech. 138, 209–247.Google Scholar
Klebanoff, P. S., Tidstrom, K. D. & Sargent, L. M. 1962 The three-dimensional nature of boundary-layer instability. J. Fluid Mech. 12, 1–34.Google Scholar
Kline, S. J., Reynolds, W. C., Schraub, F. A. & Runstadler, P. W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30, 741–773.CrossRefGoogle Scholar
Kravchenko, A. G., Choi, H. & Moin, P. 1993 On the relation of near-wall streamwise vortices to wall skin friction in turbulent boundary layers. Phys. Fluids A 5 (12), 3307–3309.Google Scholar
Mezic, I. 2005 Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41 (1), 309–325.Google Scholar
Mizuno, Y., Duke, D., Atkinson, C. & Soria, J.2011 Investigation of wall-bounded turbulent flow using dynamic mode decomposition. 13th European Turbulence Conference, vol. 318, p. 042040.Google Scholar
Moin, P. & Moser, R. D. 1989 Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 200, 471–509.Google Scholar
Nagarajan, S., Lele, S. K. & Ferziger, J. H. 2003 A robust high-order compact method for large eddy simulation. J. Comput. Phys. 191 (2), 392–419.Google Scholar
Rempfer, D. & Fasel, H. F. 1994 Evolution of three-dimensional coherent structures in a flat-plate boundary layer. J. Fluid Mech. 260, 351–375.Google Scholar
Reynolds, W. C. & Hussain, A. K. M. F. 1972 The mechanics of an organized wave in turbulent shear flow. Part 3. Theoretical models and comparisons with experiments. J. Fluid Mech. 54 (02), 263–288.Google Scholar
Rist, U. & Fasel, H. 1995 Direct numerical simulation of controlled transition in a flat-plate boundary layer. J. Fluid Mech. 298, 211–248.Google Scholar
Robinson, S. K. 1991 Coherent motion in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Rowley, C. W., Mezic, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Saric, W. S. 1986 Visualization of different transition mechanisms. In Gallery of Fluid Motion (ed. Reed, H. L.), Phys. Fluids 29, 2770.Google Scholar
Sayadi, T.2012 Numerical simulation of controlled transition to developed turbulence in a zero-pressure-gradient flat-plate boundary layer. PhD thesis, Stanford University.Google Scholar
Sayadi, T., Hamman, C. W. & Moin, P. 2013 Direct simulation of complete H-type and K-type transitions with implications for the structure of turbulent boundary layers. J. Fluid Mech. 724, 480–509.Google Scholar
Sayadi, T. & Moin, P. 2012 Large eddy simulation of controlled transition to turbulence. Phys. Fluids 24 (11), 114103–114117.Google Scholar
Sayadi, T., Nichols, J. W., Schmid, P. J. & Jovanovic, M. R. 2012 Dynamic mode decomposition of H-type transition to turbulence. In Center for Turbulence Research, Proceedings of the Summer Program, pp. 5–14.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Schmid, P. J., Violato, D. & Scarano, F. 2012 Decomposition of time-resolved tomographic PIV. Exp. Fluids 52, 1567–1579.CrossRefGoogle Scholar
Schubauer, G. B. & Skramstad, H. K. 1947 Laminar boundary layer oscillations and stability of laminar flow. J. Aeronaut. Sci. 14, 69–78.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Quart. Appl. Math. 45, 561–590.Google Scholar
Spalart, P. R. & Watmuff, J. H. 1993 Experimental and numerical study of a turbulent boundary layer with pressure gradients. J. Fluid Mech. 249, 337–371.Google Scholar
White, F. M. 2006 Viscous Fluid Flow. 3rd edn. McGraw-Hill International Edition.Google Scholar
Wu, X. & Moin, P. 2009 Direct numerical simulation of turbulence in a nominally zero-pressure-gradient flat-plate boundary layer. J. Fluid Mech. 630, 5–41.CrossRefGoogle Scholar