Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T09:44:24.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Re-entrant history force transition for stick–slip Janus swimmers: mixed Basset and slip-induced memory effects

Published online by Cambridge University Press:  06 November 2019

A. R. Premlata  and
Hsien-Hung Wei Open the ORCID record for Hsien-Hung Wei [Opens in a new window]
A. R. Premlata
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
*
†Email address for correspondence: hhwei@mail.ncku.edu.tw
Get access Rights & Permissions [Opens in a new window]

Abstract

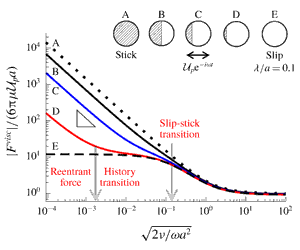
It is well known that a rigid non-slippery particle in unsteady motion can experience a Basset history force with the signature $1/\unicode[STIX]{x1D6FF}$ decay due to a Stokes boundary layer of thickness $\unicode[STIX]{x1D6FF}$. For a uniform slip particle with slip length $\unicode[STIX]{x1D706}$, however, a persistent force plateau can replace the usual Basset decay at $\unicode[STIX]{x1D6FF}$ below the slip–stick transition (SST) point $\unicode[STIX]{x1D6FF}\sim \unicode[STIX]{x1D706}$ (Premlata & Wei, J. Fluid Mech., vol. 866, 2019, pp. 431–449). Here we analyse the hydrodynamic force on an oscillating stick–slip Janus particle, showing that it can display unusual history force responses that are of neither the no-slip nor the purely slip type but mixed with both. Solving the oscillatory Stokes flow equation together with a matched asymptotic boundary layer theory, we find that the persistent force plateau seen for a uniform slip particle may be destroyed by the presence of the stick portion of a stick–slip Janus particle. Instead, a $1/\unicode[STIX]{x1D6FF}$ Basset force of amplitude smaller than the no-slip counterpart will re-emerge to dominate the high frequency viscous force response again. This re-entry Basset force, which occurs only after making a stick patch on a slippery particle, is also found to depend solely on the coverage of the stick face irrespective of the slip length of the slip face. When the stick portion is small, in particular, the re-entry Basset decay will exhibit a slip plateau on its tail, displaying a distinctive re-entrant history force transition prior to the SST. But if changing this tiny stick face to be slippery, no matter how small the slip length is, the re-entry Basset decay will disappear and a constant force plateau will return to dominate the force response again. These unusual force responses arising from mixed stick–slip or non-uniform slip effects may not only provide unique hydrodynamic fingerprints for characterizing heterogeneous particles, but also have potential uses in active manipulation and sorting of these particles.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 882 , 10 January 2020 , A7
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albano, A. M., Bedeaux, D. & Mazur, P. 1975 On the motion of a sphere with arbitrary slip in a viscous incompressible fluid. Physica A 80, 89–97.Google Scholar
Basset, A. B. 1888 On the motion of a sphere in a viscous liquid. Phil. Trans. R. Soc. Lond. A 179, 43–63.Google Scholar
Boymelgreen, A. M. & Miloh, T. 2011 A theoretical study of induced-charge dipolophoresis of ideally polarizable asymmetrically slipping Janus particles. Phys. Fluids 23 (7), 072007.Google Scholar
Crowdy, D. G. 2013 Exact solutions for cylindrical slip–stick Janus swimmers in Stokes flow. J. Fluid Mech. 719, R2.Google Scholar
Fujioka, H. & Wei, H.-H. 2018 Letter: new boundary layer structures due to strong wall slippage. Phys. Fluids 30 (12), 121702.Google Scholar
Galindo, V. & Gerbeth, G. 1993 A note on the force on an accelerating spherical drop at low-Reynolds number. Phys. Fluids A 5, 3290–3292.Google Scholar
Gatignol, R. 2007 On the history term of Boussinesq–Basset when the viscous fluid slips on the particle. C. R. Méc. 335 (9-10), 606–616.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Pergamon.Google Scholar
Laurell, T., Petersson, F. & Nilsson, A. 2007 Chip integrated strategies for acoustic separation and manipulation of cells and particles. Chem. Soc. Rev. 36 (3), 492–506.Google Scholar
Lawrence, C. J. & Weinbaum, S. 1986 The force on an axisymmetric body in linearized, time-dependent motion: a new memory term. J. Fluid Mech. 171, 209–218.Google Scholar
Lawrence, C. J. & Weinbaum, S. 1988 The unsteady force on a body at low Reynolds number; the axisymmetric motion of a spheroid. J. Fluid Mech. 189, 463–489.Google Scholar
Magnaudet, J. & Legendre, D. 1998 The viscous drag force on a spherical bubble with a time-dependent radius. Phys. Fluids 10 (3), 550–554.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Mei, R., Adrian, R. J. & Hanratty, T. J. 1991 Particle dispersion in isotropic turbulence under Stokes drag and Basset force with gravitational settling. J. Fluid Mech. 225, 481–495.Google Scholar
Michaelides, E. E. & Feng, Z.-G. 1995 The equation of motion of a small viscous sphere in an unsteady flow with interface slip. Intl J. Multiphase Flow 21 (2), 315–321.Google Scholar
Premlata, A. R. & Wei, H.-H. 2019 The Basset problem with dynamic slip: slip-induced memory effect and slip–stick transition. J. Fluid Mech. 866, 431–449.Google Scholar
Riley, N. 1966 On a sphere oscillating in a viscous fluid. Q. J. Mech. Appl. Maths. 19 (4), 461–472.Google Scholar
Stokes, G. G. 1851 On the effect of the internal friction of fluids on the motion of pendulums. Trans. Camb. Phil. Soc. 9, 8–106.Google Scholar
Sun, Q., Klaseboer, E., Khoo, B. C. & Chan, D. Y. C. 2013 Stokesian dynamics of pill-shaped Janus particles with stick and slip boundary conditions. Phys. Rev. E 87 (4), 043009.Google Scholar
Swan, J. W. & Khair, A. S. 2008 On the hydrodynamics of slip–stick spheres. J. Fluid Mech. 606, 115–132.Google Scholar
Takemura, F. & Magnaudet, J. 2004 The history force on a rapidly shrinking bubble rising at finite Reynolds number. Phys. Fluids 16 (9), 3247–3255.Google Scholar
Walther, A. & Müller, A. H. E. 2013 Janus particles: synthesis, self-assembly, physical properties, and applications. Chem. Rev. 113 (7), 5194–5261.Google Scholar
Wang, C.-Y. 1965 The flow field induced by an oscillating sphere. J. Sound Vib. 2 (3), 257–269.Google Scholar
Wang, S. & Ardekani, A. M. 2012 Unsteady swimming of small organisms. J. Fluid Mech. 702, 286–297.Google Scholar
Willmott, G. 2008 Dynamics of a sphere with inhomogeneous slip boundary conditions in Stokes flow. Phys. Rev. E 77 (5), 055302.Google Scholar
Yang, S.-M. & Leal, L. G. 1991 A note on memory-integral contributions to the force on an accelerating spherical drop at low Reynolds number. Phys. Fluids A 3 (7), 1822–1824.Google Scholar