Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-14T04:47:16.888Z Has data issue: false hasContentIssue false
  • English
  • Français

Resolvent-analysis-based design of airfoil separation control

Published online by Cambridge University Press:  26 March 2019

Chi-An Yeh Open the ORCID record for Chi-An Yeh [Opens in a new window]  and
Kunihiko Taira Open the ORCID record for Kunihiko Taira [Opens in a new window]
Chi-An Yeh*
Affiliation:
Department of Mechanical Engineering, Florida State University, Tallahassee, FL 32310, USA
Kunihiko Taira
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Los Angeles, CA 90095, USA
*
†Email address for correspondence: cayeh@seas.ucla.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We use resolvent analysis to design active control techniques for separated flows over a NACA 0012 airfoil. Spanwise-periodic flows over the airfoil at a chord-based Reynolds number of 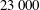$23\,000$ and a free-stream Mach number of 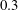$0.3$ are considered at two post-stall angles of attack of 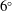$6^{\circ }$ and 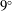$9^{\circ }$. Near the leading edge, localized unsteady thermal actuation is introduced in an open-loop manner with two tunable parameters of actuation frequency and spanwise wavelength. To provide physics-based guidance for the effective choice of these control input parameters, we conduct global resolvent analysis on the baseline turbulent mean flows to identify the actuation frequency and wavenumber that provide large perturbation energy amplification. The present analysis also considers the use of a temporal filter to limit the time horizon for assessing the energy amplification to extend resolvent analysis to unstable base flows. We incorporate the amplification and response mode from resolvent analysis to provide a metric that quantifies momentum mixing associated with the modal structure. This metric is compared to the results from a large number of three-dimensional large-eddy simulations of open-loop controlled flows. With the agreement between the resolvent-based metric and the enhancement of aerodynamic performance found through large-eddy simulations, we demonstrate that resolvent analysis can predict the effective range of actuation frequency as well as the global response to the actuation input. We believe that the present resolvent-based approach provides a promising path towards mean flow modification by capitalizing on the dominant modal mixing.

JFM classification

Flow Control: Instability control Wakes/Jets: Separated flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 572 - 610
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akins, D., Singh, A. & Little, J.2015 Effects of pulse energy on shear layer control using surface plasma discharges. AIAA Paper 2015-3344.Google Scholar
Amitay, M. & Glezer, A. 2002 Role of actuation frequency in controlled flow reattachment over a stalled airfoil. AIAA J. 40 (2), 209–216.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Beneddine, S., Sipp, D., Arnault, A., Dandois, J. & Lesshafft, L. 2016 Conditions for validity of mean flow stability analysis. J. Fluid Mech. 798, 485–504.Google Scholar
Benton, S. I. & Visbal, M. R. 2018 High-frequency forcing to mitigate unsteady separation from a bursting separation bubble. Phys. Rev. Fluids 3, 013907.Google Scholar
Bin, J., Oates, W. S. & Taira, K. 2015 Thermoacoustic modeling and uncertainty analysis of two-dimensional conductive membranes. J. Appl. Phys. 117 (6), 064506.Google Scholar
Brès, G. A., Ham, F. E., Nichols, J. W. & Lele, S. K. 2017 Unstructured large-eddy simulations of supersonic jets. AIAA J. 55 (4), 1164–1184.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (04), 775–816.Google Scholar
Chae, J., Ahn, S., Kim, H.-J. & Kim, K. H.2017 Unsteady Joule heating energy model for nanosecond pulsed DBD plasma actuator. AIAA Paper 2017-1580.Google Scholar
Choudhari, M. 1993 Boundary-layer receptivity due to distributed surface imperfections of a deterministic or random nature. Theor. Comput. Fluid Dyn. 4 (3), 101–117.Google Scholar
Chu, B.-T. 1965 On the energy transfer to small disturbances in fluid flow (Part I). Acta Mechanica 1 (3), 215–234.Google Scholar
Corke, T. C., Enloe, C. L. & Wilkinson, S. P. 2010 Dielectric barrier discharge plasma actuators for flow control. Annu. Rev. Fluid Mech. 42, 505–529.Google Scholar
Fage, A. & Johansen, F. C. 1927 On the flow of air behind an inclined flat plate of infinite span. Proc. R. Soc. Lond. A 116 (773), 170–197.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993 Stochastic forcing of the linearized Navier–Stokes equations. Phys. Fluids A 5 (11), 2600–2609.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1994 Variance maintained by stochastic forcing of non-normal dynamical systems associated with linearly stable shear flows. Phys. Rev. Lett. 72, 1188–1191.Google Scholar
Freund, J. B. 1997 Proposed inflow/outflow boundary condition for direct computation of aerodynamic sound. AIAA J. 35 (4), 740–742.Google Scholar
Garnier, E., Adams, N. & Sagaut, P. 2009 Large Eddy Simulation for Compressible Flows. Springer Science & Business Media.Google Scholar
Glezer, A., Amitay, M. & Honohan, A. M. 2005 Aspects of low- and high-frequency actuation for aerodynamic flow control. AIAA J. 43 (7), 1501–1511.Google Scholar
Goldstein, M. E. & Hultgren, L. S. 1989 Boundary-layer receptivity to long-wave free-stream disturbances. Annu. Rev. Fluid Mech. 21 (1), 137–166.Google Scholar
Gómez, F. & Blackburn, H. M. 2017 Data-driven approach to design of passive flow control strategies. Phys. Rev. Fluids 2, 021901.Google Scholar
Gómez, F., Blackburn, H. M., Rudman, M., Sharma, A. S. & McKeon, B. J. 2016 A reduced-order model of three-dimensional unsteady flow in a cavity based on the resolvent operator. J. Fluid Mech. 798, R2.Google Scholar
Greenblatt, D. & Wygnanski, I. J. 2000 The control of flow separation by periodic excitation. Prog. Aerosp. Sci. 36 (7), 487–545.Google Scholar
Häggmark, C. P., Bakchinov, A. A. & Alfredsson, P. H. 2000 Experiments on a two-dimensional laminar separation bubble. Phil. Trans. R. Soc. Lond. A 358 (1777), 3193–3205.Google Scholar
Hess, J. L. 1990 Panel methods in computational fluid dynamics. Annu. Rev. Fluid Mech. 22 (1), 255–274.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P.1988 Eddies, streams, and convergence zones in turbulent flows. Center for Turbulence Research Report CTR-S88, p. 193. NASA.Google Scholar
Hwang, Y., Kim, J. & Choi, H. 2013 Stabilization of absolute instability in spanwise wavy two-dimensional wakes. J. Fluid Mech. 727, 346–378.Google Scholar
Joslin, R. D. & Miller, D. N. 2009 Fundamentals and Applications of Modern Flow Control. American Institute of Aeronautics and Astronautics.Google Scholar
Jovanović, M. R.2004 Modeling, analysis, and control of spatially distributed systems. PhD thesis, Department of Mechanical Engineering, University of California at Santa Barbara, CA.Google Scholar
Jovanović, M. R. & Bamieh, B. 2005 Componentwise energy amplification in channel flows. J. Fluid Mech. 534, 145–183.Google Scholar
Khalighi, Y., Nichols, J. W., Ham, F., Lele, S. K. & Moin, P.2011 Unstructured large eddy simulation for prediction of noise issued from turbulent jets in various configurations. AIAA Paper 2011-2886.Google Scholar
Kim, D.-H., Yang, J.-H., Chang, J.-W. & Chung, J.2009 Boundary layer and near-wake measurements of NACA 0012 airfoil at low Reynolds numbers. AIAA Paper 2009-1472.Google Scholar
Kojima, R., Nonomura, T., Oyama, A. & Fujii, K. 2013 Large-eddy simulation of low-Reynolds-number flow over thick and thin NACA airfoils. J. Aircraft 50 (1), 187–196.Google Scholar
Lehoucq, R. B., Sorensen, D. C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.Google Scholar
Lesshafft, L. 2018 Artificial eigenmodes in truncated flow domains. Theor. Comput. Fluid Dyn. 32 (3), 245–262.Google Scholar
Little, J., Takashima, K., Nishihara, M., Adamovich, I. V. & Samimy, M. 2012 Separation control with nanosecond-pulse-driven dielectric barrier discharge plasma actuators. AIAA J. 50 (2), 350–365.Google Scholar
Liu, Q., Gómez, F. & Theofilis, V. 2016 Linear instability analysis of low-Re incompressible flow over a long rectangular finite-span open cavity. J. Fluid Mech. 799, R2.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2014 Opposition control within the resolvent analysis framework. J. Fluid Mech. 749, 597–626.Google Scholar
Luhar, M., Sharma, A. S. & McKeon, B. J. 2015 A framework for studying the effect of compliant surfaces on wall turbulence. J. Fluid Mech. 768, 415–441.Google Scholar
Marxen, O., Lang, M. & Rist, U. 2013 Vortex formation and vortex breakup in a laminar separation bubble. J. Fluid Mech. 728, 58–90.Google Scholar
McKeon, B. J. & Sharma, A. S. 2010 A critical-layer framework for turbulent pipe flow. J. Fluid Mech. 658, 336–382.Google Scholar
Moarref, R., Sharma, A. S., Tropp, J. A. & McKeon, B. J. 2013 Model-based scaling of the streamwise energy density in high-Reynolds-number turbulent channels. J. Fluid Mech. 734, 275–316.Google Scholar
Munday, P. M. & Taira, K. 2018 Effects of wall-normal and angular momentum injections in airfoil separation control. AIAA J. 56 (5), 1830–1842.Google Scholar
Nakashima, S., Fukagata, K. & Luhar, M. 2017 Assessment of suboptimal control for turbulent skin friction reduction via resolvent analysis. J. Fluid Mech. 828, 496–526.Google Scholar
Pierrehumbert, R. T. & Widnall, S. E. 1982 The two- and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 114, 59–82.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39 (1), 129–162.Google Scholar
Schmid, P. J. & Brandt, L. 2014 Analysis of fluid systems: stability, receptivity, sensitivity. Appl. Mech. Rev. 66 (2), 024803.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.Google Scholar
Schmid, P. J. & Rossi, M. 2004 Three-dimensional stability of a Burgers vortex. J. Fluid Mech. 500, 103–112.Google Scholar
Seifert, A. & Pack, L. G. 1999 Oscillatory control of separation at high Reynolds numbers. AIAA J. 37 (9), 1062–1071.Google Scholar
Sinha, A., Alkandry, H., Kearney-Fischer, M., Samimy, M. & Colonius, T. 2012 The impulse response of a high-speed jet forced with localized arc filament plasma actuators. Phys. Fluids 24 (12), 125104.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
Sun, Y., Taira, K., Cattafesta, L. N. & Ukeiley, L. S. 2017 Biglobal instabilities of compressible open-cavity flows. J. Fluid Mech. 826, 270–301.Google Scholar
Taira, K., Brunton, S. L., Dawson, S. T. M., Rowley, C. W., Colonius, T., McKeon, B. J., Schmidt, O. T., Gordeyev, S., Theofilis, V. & Ukeiley, L. S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55 (12), 4013–4041.Google Scholar
Theofilis, V. 2003 Advances in global linear instability analysis of nonparallel and three-dimensional flows. Prog. Aerosp. Sci. 39 (4), 249–315.Google Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43, 319–352.Google Scholar
Thomareis, N. & Papadakis, G. 2018 Resolvent analysis of separated and attached flows around an airfoil at transitional Reynolds number. Phys. Rev. Fluids 3, 073901.Google Scholar
Trefethen, L. N. & Embree, M. 2005 Spectra and Pseudospectra: The Behavior of Nonnormal Matrices and Operators. Princeton University Press.Google Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.Google Scholar
Vreman, A. W. 2004 An eddy-viscosity subgrid-scale model for turbulent shear flow: algebraic theory and applications. Phys. Fluids 16 (10), 3670–3681.Google Scholar
Wu, J.-Z., Lu, X.-Y., Denny, A. G., Fan, M. & Wu, J.-M. 1998 Post-stall flow control on an airfoil by local unsteady forcing. J. Fluid Mech. 371, 21–58.Google Scholar
Yeh, C.-A., Munday, P. & Taira, K.2017a Use of local periodic heating for separation control on a NACA 0012 airfoil. AIAA Paper 2017-1451.Google Scholar
Yeh, C.-A., Munday, P. M. & Taira, K. 2017b Laminar free shear layer modification using localized periodic heating. J. Fluid Mech. 822, 561–589.Google Scholar
Yeh, C.-A., Munday, P. M., Taira, K. & Munson, M. J.2015 Drag reduction control for flow over a hump with surface-mounted thermoacoustic actuator AIAA Paper 2015-0826.Google Scholar
Zaman, K. B. M. Q., McKinzie, D. J. & Rumsey, C. L. 1989 A natural low-frequency oscillation of the flow over an airfoil near stalling conditions. J. Fluid Mech. 202, 403–442.Google Scholar