Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T20:54:00.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Resonant coupling of mode-1 and mode-2 internal waves by topography

Published online by Cambridge University Press:  02 December 2020

Zihua Liu Open the ORCID record for Zihua Liu [Opens in a new window] ,
Roger Grimshaw Open the ORCID record for Roger Grimshaw [Opens in a new window]  and
Edward Johnson Open the ORCID record for Edward Johnson [Opens in a new window]
Zihua Liu*
Affiliation:
Department of Mathematics, University College London, LondonWC1E 6BT, UK
Roger Grimshaw
Affiliation:
Department of Mathematics, University College London, LondonWC1E 6BT, UK
Edward Johnson
Affiliation:
Department of Mathematics, University College London, LondonWC1E 6BT, UK
*
†Email address for correspondence: zihua.liu.15@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

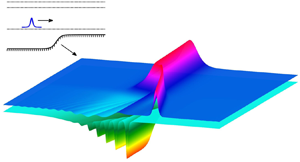
We consider the resonant coupling of mode-1 and mode-2 internal solitary waves by topography. Mode-2 waves are generated by a mode-1 wave encountering variable topography, modelled by a coupled Korteweg–de Vries (KdV) system. Three cases, namely $(A)$ weak resonant coupling, $(B)$ moderate resonant coupling and $(C)$ strong resonant coupling, are examined in detail using a three-layer density-stratified fluid system with different stratification and topographic settings. The strength of the resonant coupling is determined by the range of values taken by the ratio of linear long-wave phase speeds ($c_2/c_1$, where $c_1$ is the mode-1 speed and $c_2$ the mode-2 speed) while the waves are above the slope. In case $A$ the range is from $0.42$ (ocean edge) to $0.48$ (shelf edge), in case $B$ from $0.58$ (ocean) to $0.72$ (shelf) and in case $C$ from $0.44$ (ocean) to $0.92$ (shelf). The feedback from mode-2 to mode-1 is estimated by comparing the coupled KdV system with a KdV model. In case $A$, a small-amplitude convex mode-2 wave is generated by a depression mode-1 wave and the feedback on the mode-1 wave is negligible. In case $B$, a concave mode-2 wave of comparable amplitude to that of the depression incident mode-1 wave is formed; strong feedback enhances the polarity change process of the mode-1 wave. In case $C$, a large-amplitude concave mode-2 wave is produced by an elevation mode-1 wave; strong feedback suppresses the fission of the mode-1 wave. Simulations for a wider range of topographic slopes and three-layer stratifications are then classified in terms of these responses.

JFM classification

Geophysical and Geological Flows: Internal waves Geophysical and Geological Flows: Topographic effects Waves/Free-surface Flows: Solitary waves
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 908 , 10 February 2021 , A2
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Akylas, T. R. & Grimshaw, R. H. J. 1992 Solitary internal waves with oscillatory tails. J. Fluid Mech. 242, 279–298.CrossRefGoogle Scholar
Carr, M., Stastna, M., Davies, P. A. & van de Wal, K. J. 2019 Shoaling mode-2 internal solitary-like waves. J. Fluid Mech. 879, 604–632.CrossRefGoogle Scholar
Cheng, M.-H., Hsieh, C.-M., Hsu, J. R.-C. & Hwang, R. R. 2017 Transformation of mode-2 internal solitary wave over a pseudo slope-shelf. AIP Adv. 7 (9), 095309.CrossRefGoogle Scholar
Deepwell, D. & Stastna, M. 2016 Mass transport by mode-2 internal solitary-like waves. Phys. Fluids 28 (5), 056606.CrossRefGoogle Scholar
Deepwell, D., Stastna, M., Carr, M. & Davies, P. A. 2017 Interaction of a mode-2 internal solitary wave with narrow isolated topography. Phys. Fluids 29 (7), 076601.CrossRefGoogle Scholar
Deepwell, D., Stastna, M., Carr, M. & Davies, P. A. 2019 Wave generation through the interaction of a mode-2 internal solitary wave and a broad, isolated ridge. Phys. Rev. Fluids 4, 094802.CrossRefGoogle Scholar
Farmer, D. M. & Smith, J. D. 1980 Tidal interaction of stratified flow with a sill in Knight Inlet. Deep Sea Res. A 27 (3), 239–254.CrossRefGoogle Scholar
Gear, J. A. & Grimshaw, R. 1984 Weak and strong interactions between internal solitary waves. Stud. Appl. Maths 70 (3), 235–258.CrossRefGoogle Scholar
Griffiths, S. D. & Grimshaw, R. H. J. 2007 Internal tide generation at the continental shelf modeled using a modal decomposition: two-dimensional results. J. Phys. Oceanogr. 37 (3), 428–451.CrossRefGoogle Scholar
Grimshaw, R. 1981 Evolution equations for long nonlinear internal waves in stratified shear flows. Stud. Appl. Maths 65, 159–188.CrossRefGoogle Scholar
Grimshaw, R. 2007 Internal solitary waves in a variable medium. Ges. Angew. Math. 30, 96–109.Google Scholar
Grimshaw, R., Pelinovsky, E., Talipova, T. & Kurkina, A. 2010 Internal solitary waves: propagation, deformation and disintegration. Nonlinear. Process. Geophys. 17, 633–649.CrossRefGoogle Scholar
Helfrich, K. R. & Melville, W. K. 1986 On long nonlinear internal waves over slope-shelf topography. J. Fluid Mech. 167, 285–308.CrossRefGoogle Scholar
Helfrich, K. R. & Melville, W. K. 2006 Long nonlinear internal waves. Annu. Rev. Fluid Mech. 38, 395–425.CrossRefGoogle Scholar
Klymak, J. M. & Moum, J. N. 2003 Internal solitary waves of elevation advancing on a shoaling shelf. Geophys. Res. Lett. 30 (20), 017706.CrossRefGoogle Scholar
Lamb, K. G. & Warn-Varnas, A. 2015 Two-dimensional numerical simulations of shoaling internal solitary waves at the ASIAEX site in the South China Sea. Nonlinear Process. Geophys. 22 (3), 289–312.CrossRefGoogle Scholar
Liu, A. K., Chang, Y. S., Hsu, M.-K. & Liang, N. K. 1998 Evolution of nonlinear internal waves in the East and South China Seas. J. Geophys. Res. 103 (C4), 7995–8008.CrossRefGoogle Scholar
Liu, Z., Grimshaw, R. & Johnson, E. 2019 a Generation of mode 2 internal waves by interaction of mode 1 waves with topography. J. Fluid Mech. 880, 799–830.CrossRefGoogle Scholar
Liu, Z., Grimshaw, R. & Johnson, E. 2019 b The interaction of a mode-1 internal solitary wave with a step and the generation of mode-2 waves. Geophys. Astrophys. Fluid Dyn. 113 (4), 327–347.CrossRefGoogle Scholar
Liu, A. K., Su, F.-C., Hsu, M.-K., Kuo, N.-J. & Ho, C.-R. 2013 Generation and evolution of mode-two internal waves in the South China Sea. Cont. Shelf Res. 59, 18–27.CrossRefGoogle Scholar
Maderich, V., Jung, K. T., Terletska, K. & Kim, K. O. 2017 Head-on collision of internal waves with trapped cores. Nonlinear Process. Geophys. 24 (4), 751–762.CrossRefGoogle Scholar
Magalhaes, J. M. & Da Silva, J. C. B. 2018 Internal solitary waves in the Andaman Sea: new insights from SAR imagery. Remote Sens. 10 (6), 861.CrossRefGoogle Scholar
Maxworthy, T. 1980 On the formation of nonlinear internal waves from the gravitational collapse of mixed regions in two and three dimensions. J. Fluid Mech. 96 (1), 47–64.CrossRefGoogle Scholar
Mehta, A. P., Sutherland, B. R. & Kyba, P. J. 2002 Interfacial gravity currents. II. Wave excitation. Phys. Fluids. 14 (10), 3558–3569.CrossRefGoogle Scholar
Moum, J. N. & Smyth, W. D. 2006 The pressure disturbance of a nonlinear internal wave train. J. Fluid Mech. 558, 153–177.CrossRefGoogle Scholar
Ramp, S. R., Yang, Y. J., Reeder, D. B. & Bahr, F. L. 2012 Observations of a mode-2 nonlinear internal wave on the northern Heng-Chun Ridge south of Taiwan. J. Geophys. Res. 117, C03043.Google Scholar
Rayson, M. D., Jones, N. L. & Ivey, G. N. 2019 Observations of large-amplitude mode-2 nonlinear internal waves on the Australian North West Shelf. J. Phys. Oceanogr. 49 (1), 309–328.CrossRefGoogle Scholar
Shroyer, E. L., Moum, J. N. & Nash, J. D. 2010 Mode-2 waves on the continental shelf: ephemeral components of the nonlinear internal wave field. J. Geophys. Res. Oceans 115, C7.CrossRefGoogle Scholar
Stastna, M., Olsthoorn, J., Baglaenko, A. & Coutino, A. 2015 Strong mode-mode interactions in internal solitary-like waves. Phys. Fluids 27 (4), 046604.CrossRefGoogle Scholar
Terletska, K., Jung, K. T., Talipova, T., Maderich, V., Brovchenko, I. & Grimshaw, R. 2016 Internal breather-like wave generation by the second mode solitary wave interaction with a step. Phys. Fluids 28, 116602.CrossRefGoogle Scholar
Vanden-Broeck, J. & Turner, R. E. L. 1992 Long periodic internal waves. Phys. Fluids A 4 (9), 1929–1935.CrossRefGoogle Scholar
Vlasenko, V. I. & Hutter, K. 2001 Generation of second mode solitary waves by the interaction of a first mode soliton with a sill. Nonlinear Process. Geophys. 8, 223–239.CrossRefGoogle Scholar
Yang, Y. J., Fang, Y. C., Chang, M.-H., Ramp, S. R., Kao, C.-C. & Tang, T. Y. 2009 Observations of second baroclinic mode internal solitary waves on the continental slope of the northern South China Sea. J. Geophys. Res. Oceans 114, C10003.CrossRefGoogle Scholar
Yang, Y. J., Fang, Y. C., Tang, T. Y. & Ramp, S. R. 2010 Convex and concave types of second baroclinic mode internal solitary waves. Nonlinear Process. Geophys. 17 (6), 605–614.CrossRefGoogle Scholar
Yuan, C., Grimshaw, R. & Johnson, E. 2018 The evolution of second mode internal solitary waves over variable topography. J. Fluid Mech. 836, 238–259.CrossRefGoogle Scholar
Zhao, Z. & Alford, M. H. 2006 Source and propagation of internal solitary waves in the northeastern South China Sea. J. Geophys. Res. 111 (C11), C11012.CrossRefGoogle Scholar