Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T13:39:09.118Z Has data issue: false hasContentIssue false
  • English
  • Français

Response of a stratified boundary layer on a tilted wall to surface undulations

Published online by Cambridge University Press:  25 June 2014

Pierre-Yves Passaggia ,
Patrice Meunier  and
Stéphane Le Dizès
Pierre-Yves Passaggia
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE UMR 7342, 13384, Marseille, France ONERA, the French Aerospace lab F-92322 Châtillon CEDEX, France
Patrice Meunier*
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE UMR 7342, 13384, Marseille, France
Stéphane Le Dizès
Affiliation:
Aix Marseille Université, CNRS, Centrale Marseille, IRPHE UMR 7342, 13384, Marseille, France
*
†Email address for correspondence: meunier@irphe.univ-mrs.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The structure of a stratified boundary layer over a tilted bottom with a small streamwise undulation is studied theoretically and numerically. We show that the tilt of the boundary can induce strong density variations and wall-transverse velocities in the critical layer when the frequency of the forcing by the topography 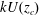$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}kU(z_c)$ is equal to the transverse Brunt–Väisälä frequency 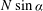$N \sin \alpha $ (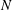$N$ being the vertical Brunt–Väisälä frequency). The viscous solution in the critical layer, obtained and compared with direct numerical simulation results, is in good agreement for both the scaling and the spatial structure. The amplitude of the transverse velocity response is also shown to exhibit quasi-resonance peaks when the stratification strength is varied.

JFM classification

Boundary Layers: Boundary Layers Geophysical and Geological Flows: Stratified flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 663 - 684
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1965 Handbook of Mathematical Functions. Dover.Google Scholar
Acheson, D. J. 1976 On over-reflection. J. Fluid Mech. 77, 433–472.CrossRefGoogle Scholar
Athanassiadou, M. & Castro, I. P. 2001 Neutral flow over a series of rough hills: a laboratory experiment. Boundary-Layer Meteorol. 101, 1–30.CrossRefGoogle Scholar
Bai, Y.2012 Rayonnement d’une couche limite dans un milieu stratifié. Master’s thesis, University Paris XI.Google Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers. McGraw-Hill.Google Scholar
Benney, D. J. & Bergeron, R. F. 1969 A new class of nonlinear waves in parallel flows. Stud. Appl. Maths 48, 181–204.CrossRefGoogle Scholar
Besio, G., Blondeaux, P., Brocchini, M. & Vittori, G. 2004 On the modeling of sand wave migration. J. Geophys. Res. 109, 1–13.Google Scholar
Boulanger, N., Meunier, P. & Le Dizès, S. 2007 Structure of a tilted stratified vortex. J. Fluid Mech. 583, 443–458.CrossRefGoogle Scholar
Boulanger, N., Meunier, P. & Le Dizès, S. 2008 Instability of a tilted vortex in stratified fluid. J. Fluid Mech. 596, 1–20.CrossRefGoogle Scholar
Candelier, J., Le Dizès, S. & Millet, C. 2012 Inviscid instability of a stably stratified compressible boundary layer on an inclined surface. J. Fluid Mech. 694, 524–539.CrossRefGoogle Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Finnigan, J. J., Shaw, R. H. & Patton, E. G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.CrossRefGoogle Scholar
Frehlich, R., Meillier, Y. & Jensen, M. L. 2008 Measurements of boundary layer profiles with in situ sensors and doppler lidar. J. Atmos. Ocean. Technol. 25, 1328–1340.CrossRefGoogle Scholar
Garratt, J. 1992 The Atmospheric Boundary Layer. Cambridge University Press.Google Scholar
Garrett, C., MacCready, P. & Rhines, P. 1993 Boundary mixing and arrested Ekman layers: rotating stratified flow near a sloping boundary. Annu. Rev. Fluid Mech. 25, 291–323.CrossRefGoogle Scholar
Genin, A., Dayton, P. K., Lonsdale, P. F. & Spiess, F. N. 1986 Corals on seamount peaks provide evidence of current acceleration over deep sea topography. Nature 322, 59–61.CrossRefGoogle Scholar
Gong, W., Taylor, P. A. & Dornbrack, A. 1996 Turbulent boundary-layer flow over fixed aerodynamically rough two-dimensional sinusoidal waves. J. Fluid Mech. 312, 1–31.CrossRefGoogle Scholar
Haberman, R. 1972 Critical layers in parallel flows. Stud. Appl. Maths 51, 139–161.CrossRefGoogle Scholar
Jackson, S. & Hunt, J. C. R. 1975 Turbulent wind flow over a low hill. Q. J. R. Meteorol. Soc. 101, 929–955.CrossRefGoogle Scholar
Lin, C. C. 1955 The Theory of Hydrodynamic Stability. Cambridge University Press.Google Scholar
Lindzen, R. S. & Barker, J. W. 1985 Instability and wave over-reflection in stably stratified shear flow. J. Fluid Mech. 151, 189–217.CrossRefGoogle Scholar
MacCready, P. & Pawlak, G. 2001 Stratified flow along a rough slope: separation drag and wave drag. J. Phys. Oceanogr. 31, 2824–2839.2.0.CO;2>CrossRefGoogle Scholar
Mahrt, L. 2014 Stably stratified atmospheric boundary layers. Annu. Rev. Fluid Mech. 46, 23–45.CrossRefGoogle Scholar
Marquillie, M. & Ehrenstein, U. 2002 Numerical simulation of a separating boundary-layer flow. Comput. Fluids 31, 683–693.CrossRefGoogle Scholar
Marquillie, M. & Ehrenstein, U. 2003 On the onset of nonlinear oscillations in a separating boundary-layer flow. J. Fluid Mech. 490, 169–188.CrossRefGoogle Scholar
Nadeau, D. F., Pardyjak, E. R., Higgins, C. W. & Parlange, M. B. 2013 Similarity scaling over a steep alpine slope. Boundary-Layer Meteorol. 147, 401–419.CrossRefGoogle Scholar
Ohya, Y. 2001 Wind-tunnel study of atmospheric stable boundary layers over a rough surface. Boundary-Layer Meteorol. 98, 57–82.CrossRefGoogle Scholar
Ohya, Y. & Uchida, T. 2008 Laboratory and numerical studies of the atmospheric stable boundary layers. J. Wind Engng Ind. Aerodyn. 96, 2150–2160.CrossRefGoogle Scholar
Park, M. S. & Park, S. U. 2006 Effects of topographical slope angle and atmospheric stratification on surface-layer turbulence. Boundary-Layer Meteorol. 147, 613–633.CrossRefGoogle Scholar
Passaggia, P.-Y., Leweke, T. & Ehrenstein, U. 2012 Transverse instability and low-frequency flapping in separated boundary-layer flows: an experimental study. J. Fluid Mech. 703, 363–373.CrossRefGoogle Scholar
Riedinger, X., Le Dizès, S. & Meunier, P. 2011 Radiative instability of the flow around a rotating cylinder in a stratified fluid. J. Fluid Mech. 672, 130–146.CrossRefGoogle Scholar
Saric, W. S., Reed, H. L. & Kerschen, E. J. 2002 Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 34, 291–319.CrossRefGoogle Scholar
Sykes, R. I. 1978 Stratification effects in boundary layer flow over hills. Proc. R. Soc. Lond. A 361, 225–243.Google Scholar
Taylor, P. A., Mason, P. J. & Bradley, E. F. 1987 Boundary-layer flow over low hills. Boundary-Layer Meteorol. 39, 107–132.CrossRefGoogle Scholar
Thorpe, S. A. 1992 The generation of internal waves by flow over the rough topography of a continental slope. Proc. R. Soc. Lond. A 439, 115–130.Google Scholar
van Haren, H. & Howarth, M. J. 2004 Enhanced stability during reduction of stratification in the north sea. Cont. Shelf Res. 24, 805–819.CrossRefGoogle Scholar
Wu, X. & Zhang, J. 2008a Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 1. Linear and nonlinear instabilities. J. Fluid Mech. 595, 379–408.CrossRefGoogle Scholar
Wu, X. & Zhang, J. 2008b Instability of a stratified boundary layer and its coupling with internal gravity waves. Part 2. Coupling with internal gravity waves via topography. J. Fluid Mech. 595, 409–433.CrossRefGoogle Scholar